一.概念和原理:因子分析法是从研究变量的内部的依赖关系出发,把一些具有错综复杂关系的变量归结为少数几个综合因子的一种多变量统计分析方法。它的基本思想是将观测变量进行分类,将相关性较高,即联系比较紧密的分在同一类中,而不同变量之间的相关性比较低,那么每一类变量实际上就代表一只基本结构,即公共因子。
可以把因子分析看作是主成分分析的推广,即可从研究相关系数矩阵内部的依赖关系出发,把一些错综复杂的关系变量归结为少数几个综合因子。研究样品间相互关系的因子关系称为Q型分析,研究变量间相互关系的因子分析成为R型因子分析。
二.因子载荷及其解释
极大似然估计法
如果假定公共因子F和特色因子ε服从整态分布,则可以得到因子载荷的极大似然估计,设估计x1,x2,...xn分布服从正态总体(u,∑)的随机样本,其中∑=AA'+D.
从似然函数理论知:
l(u,∑)=(2pi)^-np/2|∑|^-n/2e^-1/2tr[∑(xj-x)(xj-x)'+n(x-μ)(x-μ )']
(注意这里的x是x的均值)
它通过∑依赖于A和D,但上面的似然函数并不是唯一确定A,因此需要添加一下条件A'D^-1A=Λ,其中Λ是一个对角矩阵。、
可以通过数值极大化的方法可以得到A和D的极大似然估计A^ 和D^,因子分析,factanal()可以做这种估计;但是注意!函数factanal()函数是基于极大似然方法来求解的,对数据的要求比较高,通常假定数据符合多元正态分布。
因子载荷:因子载荷 aij 的统计意义就是第i个变量与第 j 个公共因子的相关系数即表示 Xi 依赖 Fj 的份量(比重)。统计学术语称作权,心理学家将它叫做载荷,即表示第 i 个变量在第 j 个公共因子上的负荷,它反映了第 i 个变量在第 j 个公共因子上的相对重要性。
因子旋转:建立因子分析的模型目的不仅仅是找出主因子,更重要的是知道每个主因子的意义,以便对实际问题进行分析。如果求出主因子后,各个主因子的典型代表变量不是很突出,还需要进行因子旋转,从而得到比较满意的因子。有两种旋转方式正交旋转(varimax),i斜交旋转。斜交旋转在日常应用中并不多见。
因子旋转就是使因子的载荷矩阵中因子载荷的绝对值向0和1两个方向分化,使大的载荷更大,小的载荷更小。在因子旋转过程中,如果因子对应轴互相正交,则成为正交矩阵。
若因子分析模型为X=AF+ε,设Γ =(γij)为正交矩阵,作为正交矩阵变换B=AΓ,可以证明,hi^2(B)=hi^2(A),gj^2(B)=∑γijgk^2(A),其中B=bij.这表明经过正交旋转后,共同度hi^2并不改变,但是公共因子的方差贡献贡献gj^2不再与原来相同。
因子得分的计算。因子分析模型建立后还有一个重要作用是应用因子分析模型去评价每个样品在整个模型中的地位,即综合评价,因子得分可以通过因子得分信息图进行展示。
概念的问题都介绍完毕,我们回顾一下步骤:
1.确认数据是否适合做因子分析
2.构造因子变量
3.旋转因子使得其更具有可解释性
4.计算因子得分并做因子图。
如何对数据进行确认是否做因子分析呢?常见方法有以下几种
(1)简单相关分析,计算原始变量的简单相关系数矩阵,如果矩阵中大部分数值过小(小于0.3),则认为大部分变量呈弱相关,不适合做因子分析;如果某个变量和其他变量相关性较弱,则可以在接来的分析中剔除该变量。 缺点:当变量很多的时候,观测起来及其不方便。
(2)偏相关分析,偏相关分析是在控制了其他变量影响的条件下计算出来的净相关系数。如果原有变量之间确实存在较强的相互重叠以及传递影响,换句话说,如果原有变量中确实能够提取公共因子,那么在控制了这些变量后的偏相关系数必然很小。
(3)KMO检验,是用于比较变量间简单相关关系和偏相关关系的指标。KMO检验统计量取值在0和1之间。如果小于0.6则认为不太合适。
(4)Bartlett's球体检验,检验的目的是判断相关矩阵是否是单位矩阵。如果是单位矩阵则认为不适合做因子分析。
一般采用KMO检验和Bartlett's球体检验进行验证。然后可以通过factanal()函数进行计算。根据累积方差贡献率确定因子的个数:如果前m个因子包含数据信息总量(即累积方差贡献率不低于80%)时,可取m个因子来反映原评价指标。然后,获得因子载荷并作出解释。根据m个因子无法确定或者实际意义不明显的时候,可以因子进行旋转来获得明显的实际意义。
概念性问题就介绍到这里了,下面我们来找个具体的案例进行感受一下。
引用一个上市公司经营业绩评价的因子分析。
library(gdata)
company=read.xls("Downloads/company.xlsx",sheet = "company")
company$上市公司<-as.numeric(company$上市公司)
fao<-factanal(company,4,rotation = "none")
fao
pairs(fao$loadings)
结果如下(没有进行旋转的)
Call:
factanal(x = company, factors = 4, rotation = "none")
Uniquenesses:
上市公司 X1 X2 X3 X4 X5
0.893 0.030 0.460 0.236 0.018 0.005
X6 X7 X8 X9 X10 X11
0.021 0.005 0.005 0.680 0.131 0.169
Loadings:
Factor1 Factor2 Factor3 Factor4
上市公司 -0.292 -0.140
X1 0.939 0.296
X2 0.714 0.148
X3 0.814 0.312
X4 0.932 0.320
X5 0.700 0.710
X6 0.707 0.688
X7 0.943 -0.325
X8 0.944 -0.319
X9 0.227 -0.333 0.392
X10 0.394 0.817 0.207
X11 0.524 -0.144 0.732
Factor1 Factor2 Factor3 Factor4
SS loadings 3.501 3.233 1.373 1.244
Proportion Var 0.292 0.269 0.114 0.104
Cumulative Var 0.292 0.561 0.676 0.779
Test of the hypothesis that 4 factors are sufficient.
The chi square statistic is 91.56 on 24 degrees of freedom.
The p-value is 7.95e-10
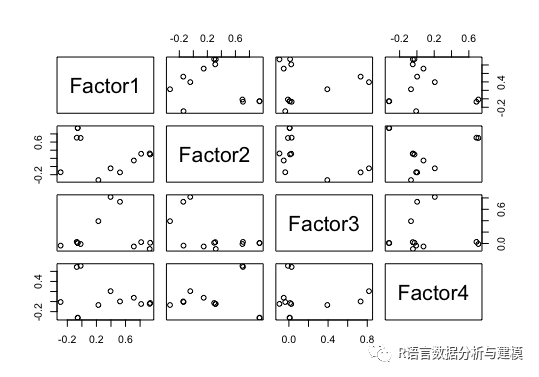
接下来进行因子旋转
fao1<-factanal(company,4,rotation="varimax")
fao1
pairs(fao1$loadings)
结果如下:
Call:
factanal(x = company, factors = 4, rotation = "varimax")
Uniquenesses:
上市公司 X1 X2 X3 X4 X5
0.893 0.030 0.460 0.236 0.018 0.005
X6 X7 X8 X9 X10 X11
0.021 0.005 0.005 0.680 0.131 0.169
Loadings:
Factor1 Factor2 Factor3 Factor4
上市公司 -0.303
X1 0.959 0.105 0.192
X2 0.723 0.102
X3 0.843 0.151 0.171
X4 0.980 0.115
X5 0.133 0.967 0.193
X6 0.959 0.227
X7 0.162 0.223 0.948 -0.149
X8 0.162 0.228 0.947 -0.150
X9 -0.236 -0.199 0.470
X10 0.198 0.150 0.896
X11 0.319 0.846
Factor1 Factor2 Factor3 Factor4
SS loadings 3.427 2.056 1.986 1.882
Proportion Var 0.286 0.171 0.165 0.157
Cumulative Var 0.286 0.457 0.622 0.779
Test of the hypothesis that 4 factors are sufficient.
The chi square statistic is 91.56 on 24 degrees of freedom.
The p-value is 7.95e-10
> pairs(fao1$loadings)
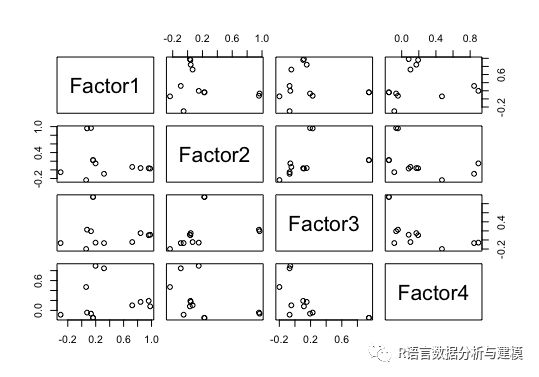
从图中可以看到四个因子的方差贡献率达到80%左右,所以只要取前面四个因子就可以较好的概括原始指标。
从通过正交旋转后的因子中可以看到因子载荷矩阵F1在x1,x2,x3,x4的载荷量比较大。F2在x5,x6的载荷量比较大。F3在x7,x8的载荷量比较大。F4在x10,x11的载荷量比较大






