

内容概要


文章主要研究了展示广告中的实时竞价优化问题。RTB允许广告主对实时的展示广告曝光进行竞价,对广告平台而言,一个基本的技术挑战是如何根据预算、广告投放目标、以及实时和历史信息自动化投放过程。本文将程序化竞价问题转化为一个函数优化问题,在一定的相关性假设下,得到了可以实时计算的简单竞价函数
文章名称:Optimal Real-Time Bidding for Display Advertising


业务流程及问题描述


实时竞价已经成为展示广告中的一种主流出价方式。本小节以程序化交易平台为例,简要描述一下广告业务流程
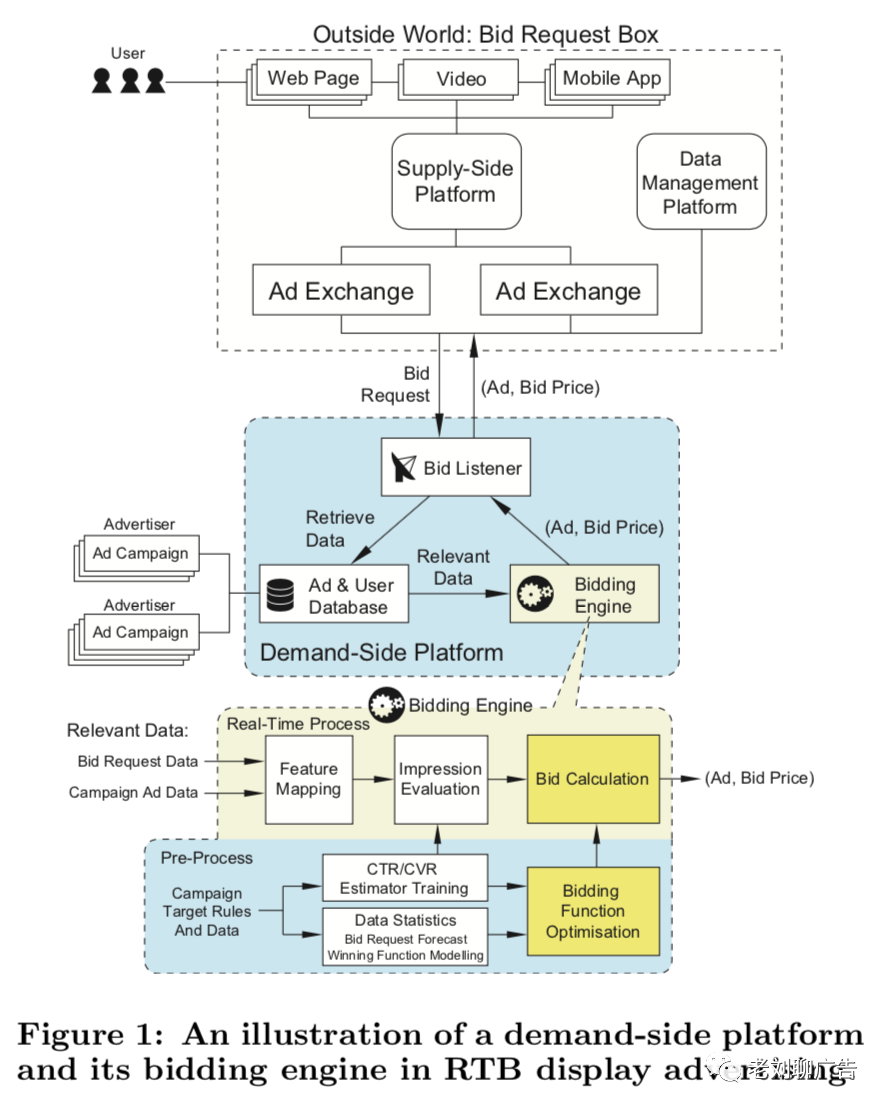
用户访问网页、视频或者APP,产生广告曝光,从而产生一个或多个广告请求
广告请求信息首先会到达SSP,即供给方平台。SSP根据收益动态决定广告请求分配到自运营广告库、其它广告网络还是DSP
如果决定将广告售卖给DSP,则通过ADX,即广告交易平台给DSP发送出价请求
DSP在收到竞价请求后,会从所有活动中找到符合条件的广告创意,并计算每个广告创意的竞价,并将出价返回给交易平台
最终,获胜者会被通知通过媒体向用户展示它的广告
这个竞价计算逻辑,即竞价策略,是DSP中最重要的部分。在广义二价拍卖机制中,广告主理论上的最优策略是实话实说:即根据自己对曝光的预估去出价。当一个竞价请求到来时,DSP会预估它的点击/转化率,并将其乘以点击/转换的价值,许多广告主在整个投放活动中把这个作为他们的出价
然而,如果希望优化广告投放活动的整体性能,在计算竞价出价时,需要考虑实际的限制因素,如出价的预期曝光、总预算以及投放活动剩余时间等
基于以上问题,文章将曝光竞价策略定义为竞价出价的映射,提出了一种新的函数优化框架来求解最优竞价函数


问题定义


以下是文章接下来的内容用到的符号
在展示广告中,广告主上传他们的广告创意,设定目标(如用户细分、时间和地点等)和在整个广告活动声明周期内的预算。在广告主设定目标后,广告平台为了获取一些统计数据,会首先花费少量预算对随机曝光进行竞价。之后就可以使用积累的数据提取每个竞价请求的特征向量来预测,主要包含两类特征:一类是从广告活动本身提取的;一类是从曝光信息中提取的,用户的cookie信息、位置、时间、用户终端、浏览器、上下文信息等。不同的广告主可能会考虑不同的指标,例如一个广告活动的目标是最大化点击数,那么;如果广告活动的目标是转化率,那么
接下来,我们的目标就是在预测指标的基础上,设计一个最优的竞价策略,以使得某个指标最大化。为了方便叙述,我们以点击数作为广告投放活动的目标。数学上,我们的实时最优竞价问题可以用下面的函数优化问题来表示:
在等式(1)中,和的乘积表示曝光拍卖中的点击可能性。在特征空间中对其求微分可以得到每次曝光拍卖中的预期点击。这个约束是由期望成本的上界构成的,RTB通常采用广义第二价格拍卖。然而,由于保留价的设定,其成本往往高于第二高的出价。因此,我们使用竞价价格作为获胜成本的上限。具体地说,成本和获胜率的乘积构成了每个曝光拍卖的预期成本,将其在特征空间上求积分,并乘以NT可以得到预期成本,该预期成本应不大于预算B。通过在预算约束下最大化点击数,eCPC就会最小化,这在展示广告中是非常重要的指标
为了上述问题可以解决,我们做了如下假设:
假设,这个等式代表着的转换。这使得在很大程度上减少了需要优化的函数决策空间,同时仍然能够通过预估指标获得曝光特征的依赖性 假设。这使得特征只能通过它生成的出价来影响获胜率。因为我们发现,获胜概率对竞价请求特征的依赖性远小于竞价价格
因此,优化问题被重写为如下形式:
此外,由于和之间存在确定性关系,因此,它们的概率密度关系也确定了:
这样我们就可以通过代换来对求积分了:
最终的函数优化问题可以改写为下:


优化方案


目标函数(5)的拉格朗日函数如下式:
其中,是拉格朗日乘子。根据变分法,的欧拉-拉格朗日条件是:
可以看出,预测指标的概率密度已经被剔除掉了,竞价函数的形式仅取决于获胜函数。这主要是因为目标和约束函数都是对的分布进行积分。不同的获胜函数会获得不同的最优竞价函数,这里我们给出了两个典型的、拟合真实世界数据曲线的获胜函数,并推导出它们的最优竞价函数形式


获胜&竞价函数1


我们的实验在真实数据集上进行,获胜率始终呈现凹形:当出价较低时,增加一个单位的出价相比于出价较高时能够获得更多的获胜率。因此,一个简单的获胜函数形式是:
其中是一个常量。对出价求导得:
将公式(9)和公式(10)代入公式(8)得:
求解上面公式可以得到我们最终的最优竞价函数:
在假设获胜函数是公式(9)的前提下,最优竞价函数是一个凹的平方根函数形式。在固定时,图2(b)展示了竞价函数在c取不同值时的曲线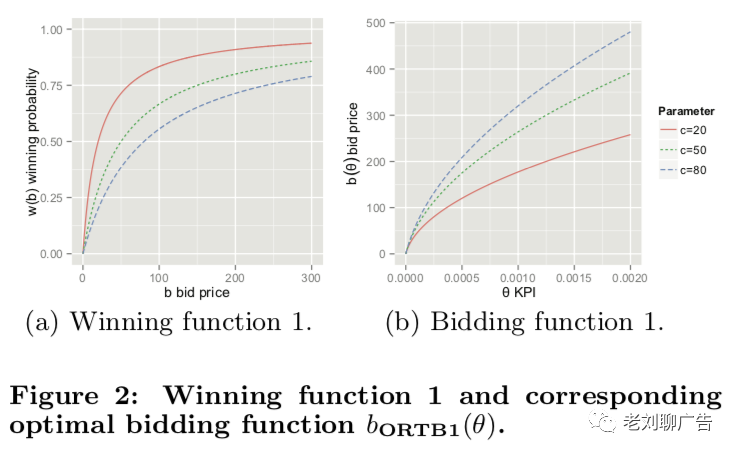


获胜&竞价函数2


对于一些有竞价目标的广告活动,或者媒体设置了较高的保留价,当出价在0左右时,获胜的概率不会迅速增加。只有当出价大于某一非零值时,获胜概率才开始增加。为了把这个情况考虑进来,我们提出了一个新的获胜函数:
参数控制曲线的递增点。利用同样的方法可以计算得到最优竞价函数:
我们的优化框架是一个通用框架:式(8)表明不同的获胜函数将会产生不同的最优竞价函数。该框架可以通过不同的获胜函数来适应不同的广告市场

欧阳修
以自然之道,养自然之身。


点个在看你最好看






