如果矩阵A中m等于n,称为矩阵A为n阶矩阵(或n阶方阵)
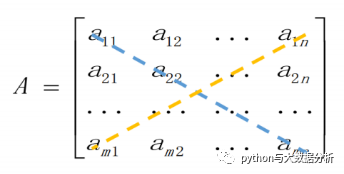
从左上到右下的对角线为主对角线,从右上到左下的对角线为次对角线
行列式在数学中,是一个函数,其定义域为det的矩阵A,取值为一个标量,写作det(A)或 | A | ,可以看作在几何空间中,一个线性变换对“面积”或“体积”的影响。
行列式的性质:
性质1:如果(a,b)=(1,0),(c,d)=(0,1)则平行四边形变成正方形,面积=1,A为单位阵
性质2:若A有相同的两行,则det(A)=0. 看一个极端情况,如果(a,b)=(c,d),即向量(a,b)与(c,d)重合,面积肯定为0。
性质3:det(A)对单独任一行满足线性关系,即将(a,b)伸缩t倍,另一条边不变,面积也伸缩t倍
性质4:交换两行,det(A)变号。将面积定向处理,右手定则是大家普遍遵守的,因此,行1,行2对应向量的方向满足右手定则,则定义det(A)为正,否则为负。
性质5:若矩阵中有一行为全0行,则行列式为0.利用性质3,全0行,提出一个因子0,行列式肯定为0.
性质6:从一行中减去其它行的几倍,行列式不变。
性质7:若矩阵A为三角阵,则行列式等于对角元上元素的乘积。
性质8:A是奇异阵且不可逆,行列式为0;反之,行列式不为0。
性质9:矩阵AB的行列式等于A的行列式乘以B的行列式行列式的含义是面积(体积)的放大倍数,AB可以看成是级联系统,级联系统的放大倍数等于分别每一级放大倍数的乘积。
性质10:A转置的行列式等于A的行列式。行列式的含义是体积的放大倍数,转置后,体积放大倍数也没有发生变化。


假设为3*3的方阵
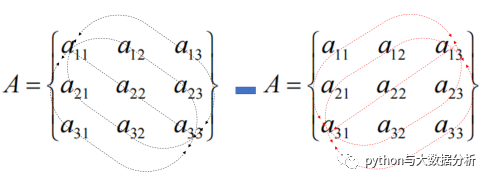
A = a13a21a32 + a12a23a31 + a11a22a33 - a11a23a32 - a12a21a33 - a13a22a31
代数余子式求法

具体推导如下:
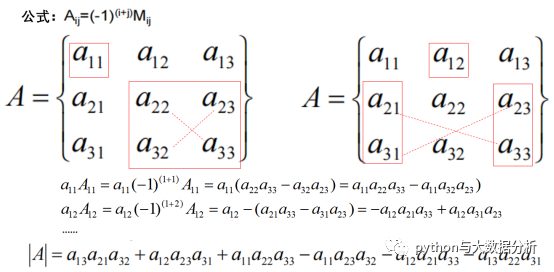
设A是一个n阶矩阵,若存在另一个n阶矩阵B,使得:AB=BA=E ,则称方阵A可逆,并称方阵B是A的逆矩阵。如果A不存在逆矩阵,那么A称为奇异矩阵。A的逆矩阵记作A-1。
矩阵的逆具有以下性质:
如果矩阵A是可逆的,那么矩阵A的逆矩阵是唯一的。
A的逆矩阵的逆矩阵还是A,记作(A-1)-1=A
可逆矩阵A的转置矩阵AT也可逆,并且(AT)-1=(A-1)T
若矩阵A可逆,则矩阵A满足消去律,即AB=AC => B=C
矩阵A可逆的充要条件是行列式|A|不等于0
逆矩阵求解公式:
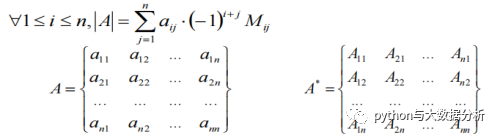
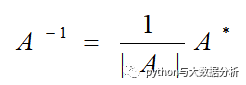
求解线性方程组
一、消元法
二、矩阵的初等变换求解






