关于矩阵的秩及求解Python求法

关于消元法求解线性方程组

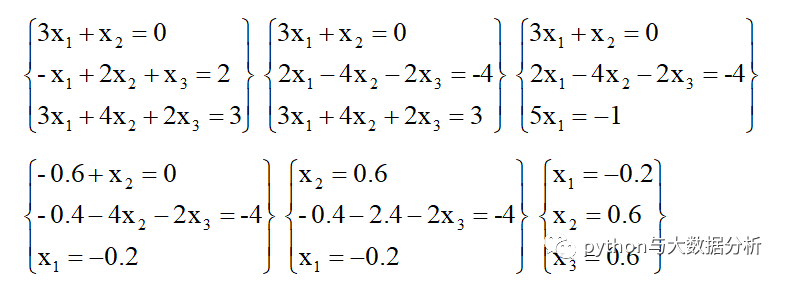
可将系数和结果转换为矩阵，并可令B为增广矩阵

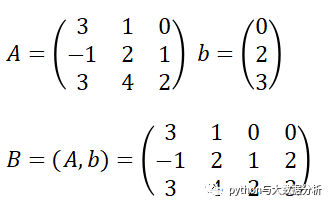
 将A、B通过消元法求解

所有的m*n的矩阵经过一系列初等变换，都可以变成如下的形式：

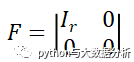
r就是最简矩阵当中非零行的行数，它也被称为矩阵的秩。我们把A矩阵的秩记作: R(A),那些方程组中真正是干货的方程个数，就是这个方程组对应矩阵的秩，阶梯形矩阵的秩就是其非零行数！

一个矩阵经过初等变换，它的行列式保持不变。如果行列式当中存在某一行或者某一列全部为0，那么它的行列式为0。

因此，对于n阶矩阵A而言，如果它的秩R(A)<n，那么|A|=0。

可逆矩阵的秩就等于矩阵的阶数，不可逆矩阵的秩小于矩阵的阶数。所以，可逆矩阵又称为满秩矩阵，不可逆矩阵又称为降秩矩阵。

线性方程组的解

我们理解了矩阵的秩的概念之后，看看它在线性方程组上的应用。

假设当下有一个n元m个等式的方程组：

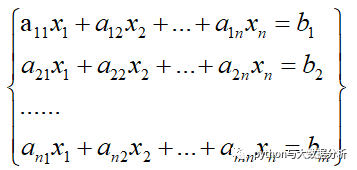
我们可以将它写成矩阵相乘的形式：Ax = b

其中A是一个m*n的矩阵，  

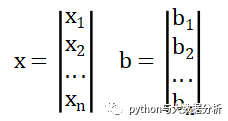
我们利用系数矩阵A和增广矩阵B=(A,b)的秩，可以和方便地看出线性方程组是否有解。我们先来看结论：

当R(A) < R(B)时无解

当R(A) = R(B) = n时，有唯一解

当R(A) = R(B) < n时，有无数解

#!/usr/bin/env python# -*- coding: UTF-8 -*-#                     _ooOoo_#                   o8888888o#                    88" . "88#                 ( | -  _  - | )#                     O\ = O#                 ____/`---'\____#                  .' \\| |// `.#                  \\|||:|||// \#                _|||||-:- |||||- \#                | | \\\ -  | |#              | \_| ''\---/'' | _/ |#               \ .-\__ `-` ___/-. #            ___`. .' --.--\ `. . __#         ."" '< `.___\_<|>_/___.' >'"".#       | | : `- \`.;`\  _ `;.`/ - ` : | |#          \ \ `-. \_ __\ __ _/ .-`  #      ==`-.____`-.___\_____/___.-`____.-'==#                     `=---=''''@Project ：pythonalgorithms @File ：Rankofmatrix.py@Author ：不胜人生一场醉@Date ：2021/8/22 22:56 '''import numpy as npA = np.array([[3, 1, 0], [-1, 2, 1], [3, 4, 2]])b = np.array([0, 2, 3])B = np.array([[3, 1, 0, 0], [-1, 2, 1, 2], [3, 4, 2, 3]])# A的秩print("A的秩为{}".format(np.linalg.matrix_rank(A)))# A的秩为3# B的秩
print("B的秩为{}".format(np.linalg.matrix_rank(B)))
# B的秩为3
# 求解方程
x = np.linalg.solve(A, b)
print("x={}".format(x))
# x=[-0.2  0.6  0.6]
# 可将结果带入验证方程
# 3*-0.2 + 1*0.6 + 0*0.6 = 0
# -1*-0.2 + 2*0.6 + 1*0.6 = 2
# 3*-0.2 + 4*0.6 + 2*0.6 = 3