在上一篇《「召回层」如何评估召回效果?》)中介绍召回层常用的效果评估
方法。本文将介绍在线实验中最常用的A/B Testing
。
预告:
下一篇我们将一起来回顾下常用的假设检验方法。感兴趣的同学别忘了点个关注哦!
一、什么是A/B Testing
简单来说,A/B Testing是将用户分成不同的组,同时对不同组的用户测试不同方案,通过用户真实反馈来找到较好方案的过程。用于解决多种方案择优的问题
。
A/B Testing的优势主要有:
快迭代:通过同时进行多组A/B Testing实验,快速验证方案效果,加快产品迭代速度 低风险:采用小流量实验,对大盘整体影响小,降低了新策略对线上用户的影响,风险低 低成本:A/B Testing实验创建、维护简单,线上用户反馈真实可靠,实验成本低
在做A/B Testing时的核心原则:
单次实验仅评估单一因素:一次实验不要引入多个影响因素,否则会导致实验效果无法区分是哪个因素影响的。
二、A/B Testing适合干什么
1、适合干什么
A/B Testing是一种用来验证所提出的改进方案是否有效的方法,从统计学意义上说是一类假设验证的方法。其主要是基于产品当前状态,来验证哪个方案更好,即A/B Testing可以帮助产品从1到10,但是无法实现从0到1创造产品。
对于推荐领域,A/B Testing主要用于:各种优化(如算法、策略、模型)的效果对比评估,从而帮我们快速实现迭代。如,离线验证有效的新模型,切小流量上线验证其效果
2、不适合干什么
虽然A/B Testing应用广泛,但并非万能的,例如下面场景就不适合使用A/B Testing:
创造新的方案:A/B Testing能告诉我们当前多种方案中哪个更好,但不能告诉我们世上最好的方案是什么
需要进行很长时间测试才能得到结果:如哪种策略能提升用户的二次消费(如换手机、再次出国旅游、换车等)
测试功能的完整性
用户量太少的场景
总之:A/B Testing无法预测要爬哪座山峰,但是可以测试出通过哪条路能更快登上峰顶
。
三、A/B Testing基本流程
A/B Testing是一个不断循环渐进的过程,主要流程如下图所示:
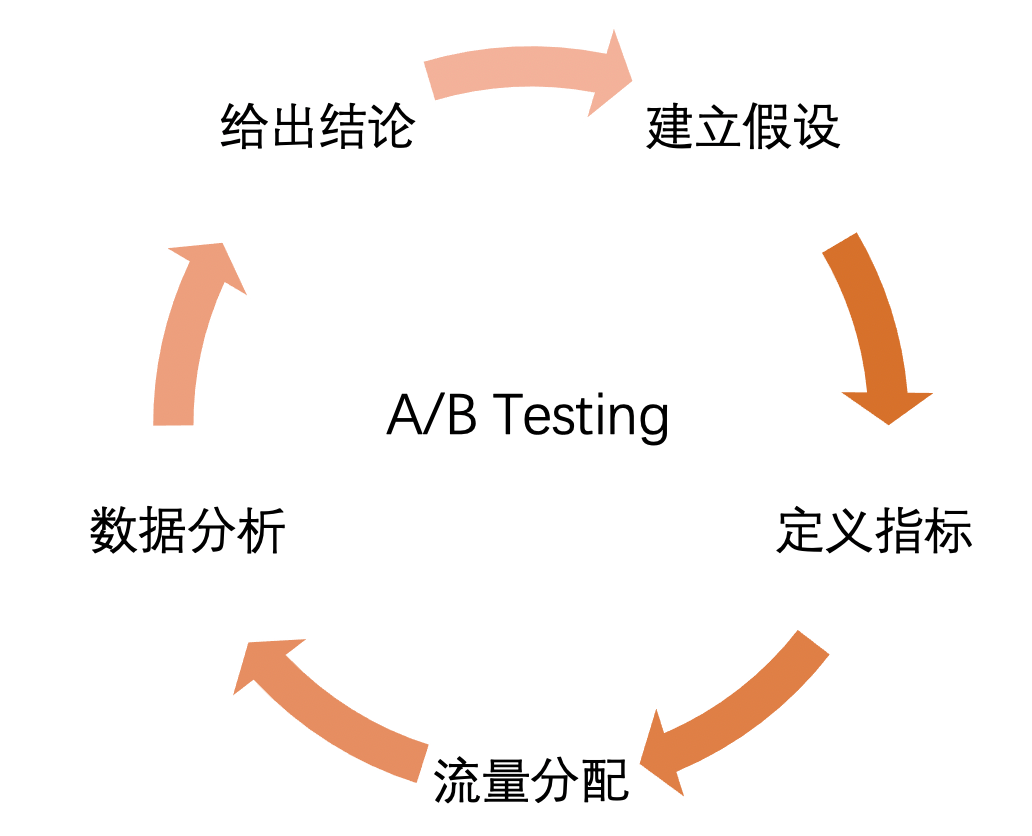
建立假设:实验开始之前要明确实验目标和预期(如新模型能显著将CTR提升3个点、时长能达到1小时等)。假设的来源是多种多样,可以基于线上用户反馈,也可以基于某位算法大佬的论文等。当然也可以是开发、产品、测试所提出假设; 定义指标:设置核心指标(如CTR、时长等)来衡量方案的优劣;同时可以设置辅助指标来评估其他的影响; 流量分配:给各实验组分配相应的流量,主要原则是 均匀
、随机
、用户唯一
、样本充足
。这样实验结果才更真实可靠和稳定;数据分析:通过数据上报、收集、统计用户反馈数据,采用统一口径,明确结果是否正向,并确保数据的可靠性。最后采用假设检验方法,检验指标是否符合预期; 给出结论:基于数据分析的结果,给出本次实验的结论,如确认新模型上线、调整流量分配继续测试、继续优化方案重新测试等;
A/B Testing虽然流程相对较多,但其重点在于:1)如何给各实验组分配流量;2)如何验证有效性(即假设检验)。
四、流量怎么分配
1、流量分配原则
流量分配是将用户分配到对应实验组的过程。流量分配通常有如下原则:
均匀:两个实验组里的用户的抽样要尽可能分布均匀、属性一致。如果分布不均匀,就容易造成辛普森悖论; 随机:在满足均匀和实验需求的情况下,对用户的抽样要尽可能随机。如使用HASH算法根据用户ID进行取模,选取其中的一部分进行抽样; 用户唯一:在一个A/B Testing实验中,用户最多只能被分配到一个实验组中; 样本充足:样本过小会造成实验数据波动过大,从而不置信或者导致实验周期过长,最终影响实验的分析效率。因此要尽量保证每个实验组中有充足的样本(后面会将如何计算所需的最小样本)。
了解流量分配的基本原则之后,通常需要考虑给每个实验组分配多少流量。通常对于不同目标的实验,流量分配会有如下规律,如下图示:
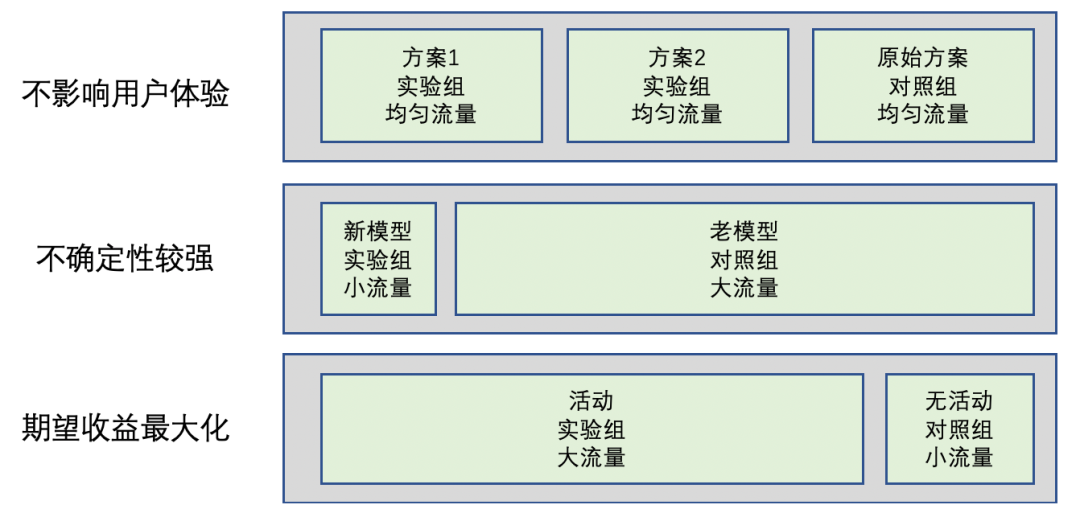
对于不影响用户体验的实验,一般给各实验组和对照组分配相当量级的流量,如UI、文案之类的实验; 对于不确定性较强的实验,一般会采用小流量(如5%的流量)实验,主流量还是集中在现网版本。当实验有结论之后再考虑一步步给实验组放量。如新版本上线、新推荐模型上线等; 对于期望收益最大化的实验,一般给实验组分配大流量,留出小部分流量作为对照组来评估收益,如活动运营、热点事件运营等。
2、流量分层:多层重叠
通常A/B Testing系统会同时有多个实验进行,仅在同一层考虑流量分配是无法满足实验的流量需求的,而且这样流量的利用率也不高,那如何解决呢?
Google提出了多层重叠实验(这也是目前业内主流的方式)。多层重叠实验引入了域和层的概念:
域:对用户流量纵向划分,将流量垂直切分成多域,域间实现互不干扰,保证实验纯度。 层:对域内流量横向划分,每层使用独立的Hash函数对用户进行分桶,使得层间的用户流量是正交的。
简言之就是:域间隔离,层间正交,如下图所示:
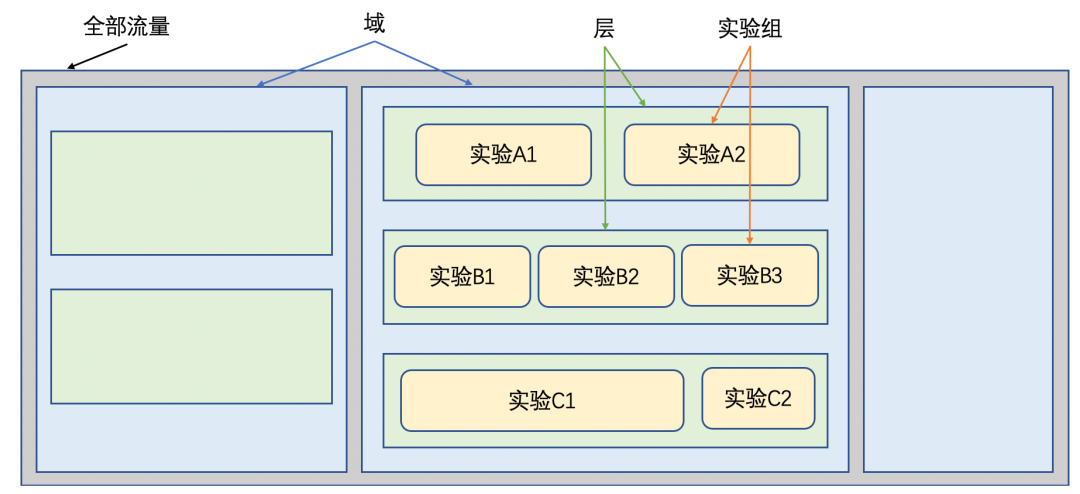
如果实验是能相互影响的(如实验A1外层的排序模型,实验A2是内层的关联推荐模型),两个实验室需要设置为互斥实验,应放在同一层中。
如果实验间无影响(如UI、搜索、广告推荐实验),可以在不同层进行实验,增加流量的利用率。
3、实验组样本量选取
在做实验时需要确保实验组有充足的样本,才能保证实验结果的可靠性:
实验样本过大,会浪费流量资源和实验时间,还可能会影响现网用户体验 实验样本过小,得到的数据效果不能支撑结论, 实验结果不可信,浪费了实验时间
因此,如何快速的获得可靠的实验结果,实验样本分配是很关键的一步:应尽量在最小样本基础上使用较少样本。下面我们就来看下,如何根据实验预期结果和大盘用户量,来确定实验所需的最小样本。
在统计学中,最小样本量计算如下:
其中,
是每组所需最小样本量,因为一个A/B Testing实验会有多个实验组(假设个实验组),整个实验所需样本量为 和分别是预设的 第一类错误概率
和第二类错误概率
(具体含义下一节会讲)为正态分布的分位数函数(可以通过查表得到) 为两组数值的差(如点击率从1%到1.5%,那么就是0.5%) 为标准差,越大表示数值波动越厉害。
从公式可以看出,其他条件不变的情况下,如果实验两组数值差异越大或者数值的波动性越小,所需要的样本量就越小。
在实验中经常需要比较两个方案哪个更好,通常设置的指标有两大类:比率型(如点击率、完播率、点赞率等)和均值类(如人均播放时长、人均观看条数等)。对于这两大类的指标,分别采用如下方法来计算实验所需的最小样本量:
A) 比率型
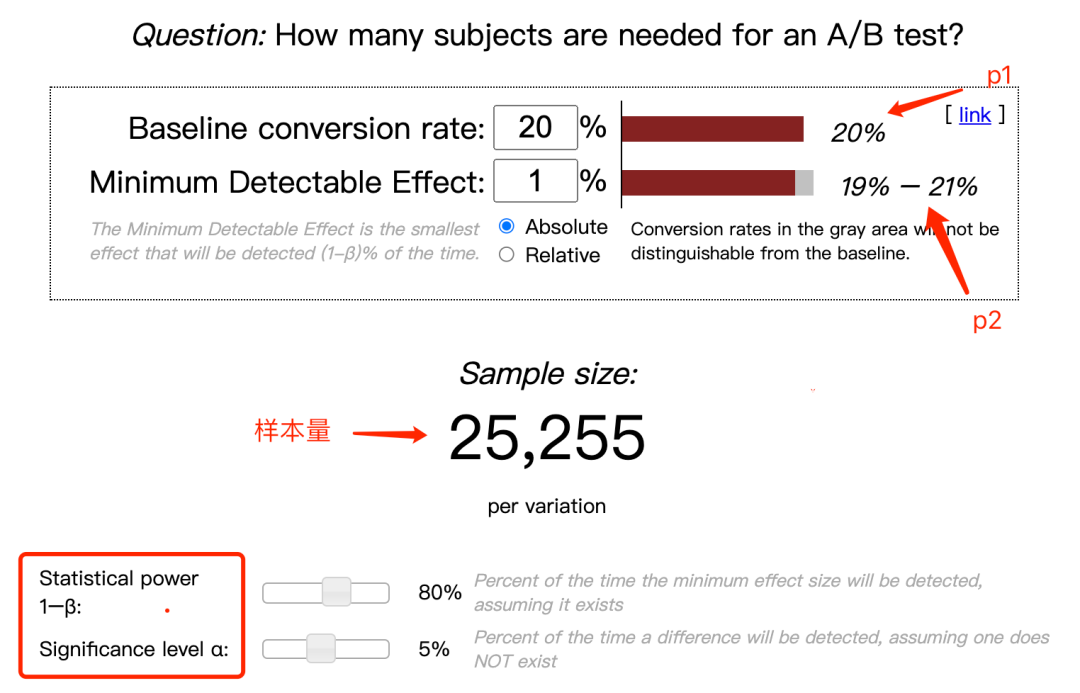
假设,和分别表示基础指标(对照组)和目标指标(实验组),和,有个实验组,则对照组和实验组最小样本和如下:
也可以通过这个网站在线计算:https://www.evanmiller.org/ab-testing/sample-size.html
B) 均值型
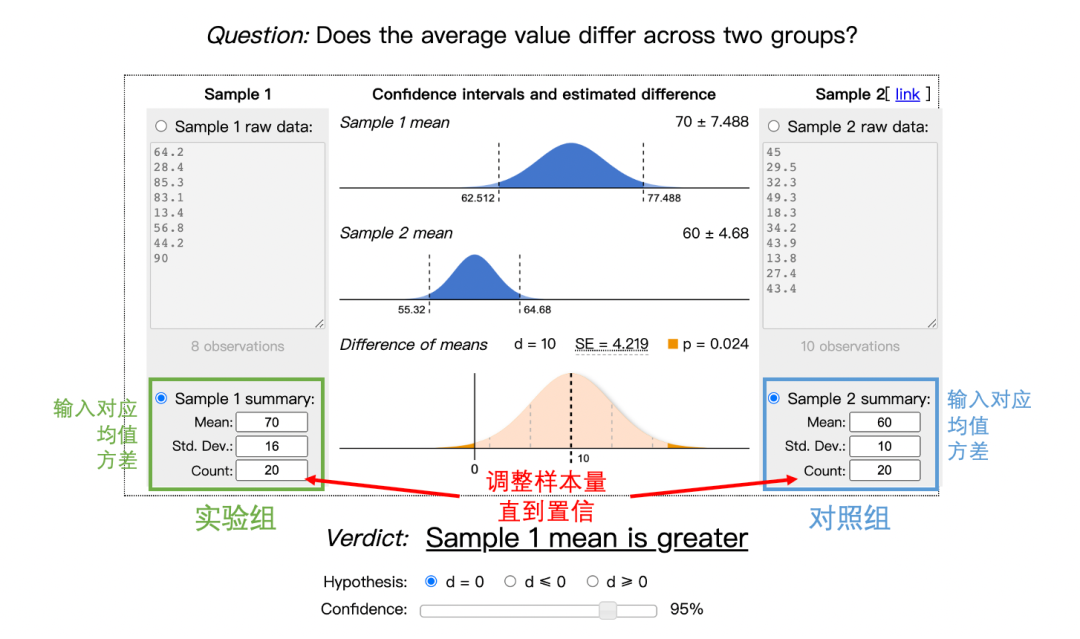
假设和分别表示对照组和实验组的均值,和分别表示对照组和实验组的标准差,和,有个实验组,则对照组和实验组最小样本和如下:
也可以通过这个网站在线计算:https://www.evanmiller.org/ab-testing/t-test.html
至此,我们实现了对不同类型评估指标的实验最小样本的计算。后续就能直接采用实验数据来分析实验的有效性。
五、假设检验
假设检验的一般过程为:
提出假设,也称之为零假设(H0),与之对应的否命题被称为备择假设; 在零假设成立的条件下,构造统计量,并确定其分布 基于统计量和分布,可以有两种方案来考量:1)确定计算出来的值是否落在拒绝域内;2)计算出零假设成立的概率值
在假设检验的过程中会出现以下情况:

在实验时,我们希望尽可能控制第一、二类错误。
1、第一类错误
第一类错误是:原假设为真时拒绝了原假设
。
在实际应用中,这是我们很容易犯的是错误,也就是2个方案无差异的,我们错误的认为他们有差异(如上线的新模型并没有显著提升指标,但我们最终一厢情愿的相信它确实对指标有显著提升)。
对第一类错误的假设检验称为显著性检验
,通过p-value
来判断。p-value
为值的概率值(可以查表),是样本所提供的证据对H0支持程度的度量,p-value
越小说明反对H0的证据越多。通常通过指定显著性水平来控制出错概率(一般取或)。当p-value<=α
时,拒绝H0。
显著性水平是指我们能容忍的最低误判概率(即第一类错误)。例如,表示在某个同分布模型产生100份的数据集中进行逐一检验,只允许出现一次误判。
p-value
表示在H0成立所对应的模型下,出现实验样本的概率。以抛硬币为例,H0:两面概率相等。如果抛10次,正面出现了8次,其概率为0.044()。如果,就不能拒绝H0,如果,就可以拒绝H0。因此,
p-value
是根据实验数据计算得出,而是人为指定的,代表你对检验错误率的一种阈值设定。
2、第二类错误
第二类错误是:原假设为假时接受了原假设
,也就是2个方案有差异时,我们认为他们没有差异。通常将发生第二类错误的概率记为 ,不犯第二类错误的概率为的。
当H0为假时,做出拒绝H0的结论的概率(即)称之为检验功效
,通常最低的统计功效值为80%
。
综上,通常情况下,A/B Testing实验的有效性要保证:95%以上的置信水平,0.05以下的显著性水平以及80%检验功效
。
最后
对于从事推荐工作的同学来说,采用A/B Testing能快速帮我们评估模型线上的有效性,从而实现模型的快速迭代。因此,了解A/B Testing的基本原理和方法也是做推荐的一个必备技能。
参考文献
[1] Jiange Liu: 如何设计一个 A/B test?
[2 ] How many subjects are needed for an A/B test?
[3] Does the average value differ across two groups?
[4] Wikipedia: Statistical hypothesis testing






