哈希表索引适合点查询(根据KEY,得到VALUE这种精准查询),不适用于范围查询。为了实现范围查询与模糊查询,数据库中引入了表级索引(TABLE INDEX),例如后面要介绍的B树就是一种表级索引。
表级索引作为表中数据的一个副本,其依据部分属性对数据重新排序组织,用于数据的快速访问。表级索引在范围查询的时候可以快速得到满足条件的所有的key。
表级索引需要与数据的存储保持一致,数据在磁盘上增删改操作需要同步到索引上。例如,当用户INSERT数据的时候,索引中也会添加条数据,而这对于上层成程序员来说是透明的。
7.2 Balanced(B) Tree Family
B 树中的 B 表示 Balance 的意思,即能够保证左右子树的平衡度。现代数据库中 B+ 树和 B 树两个词有时候会混用,例如PostgreSQL文档中说使用的B 树,但是实际是B+ 树。
B 树的一个重要特点是,当往 B 树中插入数据时,其永远能够保证节点内部和节点之间数据有序。利用这一性质我们能够根据B 树索引进行高效的检索,且时间复杂度为log(N)。
1. B+树被认为是一种多路查询树(M-way search tree),树的根节点有M条路径到达其他节点。
2. 永远能够保持平衡性,任意两个左右子树的深度相同,保证任何叶子节点到跟节点距离相同。
3. 每个节点都是半满的状态,节点管理的KEY个数至少为M/2-1且小于M,B+ 树也根据这个来控制平衡度。
下图是课程中给出的一个B+ 树示例:
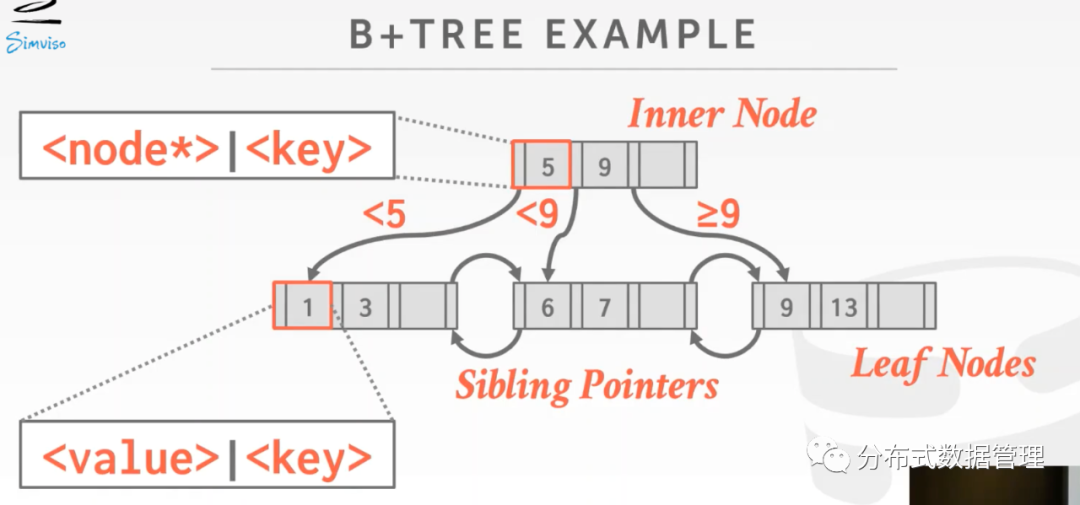
1. Inner Node中存放指针,Leaf Node中存放tuple(或者Record ID)。
2. 第一个叶子节点中存放的都是KEY小于5的数据,第二个叶子节点中存放KEY小于9大于等于5的数据,第三个叶子节点中存放KEY大于等于9的数据。
3. 叶子节点之间有双向指针互联(这也是B Link 树的设计)
4. 由于B/B+树能够保证每个节点中数据有序,因此对于Inner Node我们可以根据KEY来判断继续从左孩子搜索还是右孩子检索。对于Leaf Node我们可以根据KEY判断数据是否是满足Range Query的条件,然后利用Leaf Node之间的双向指针来线性检索。
B+ Tree 叶子节点的实现
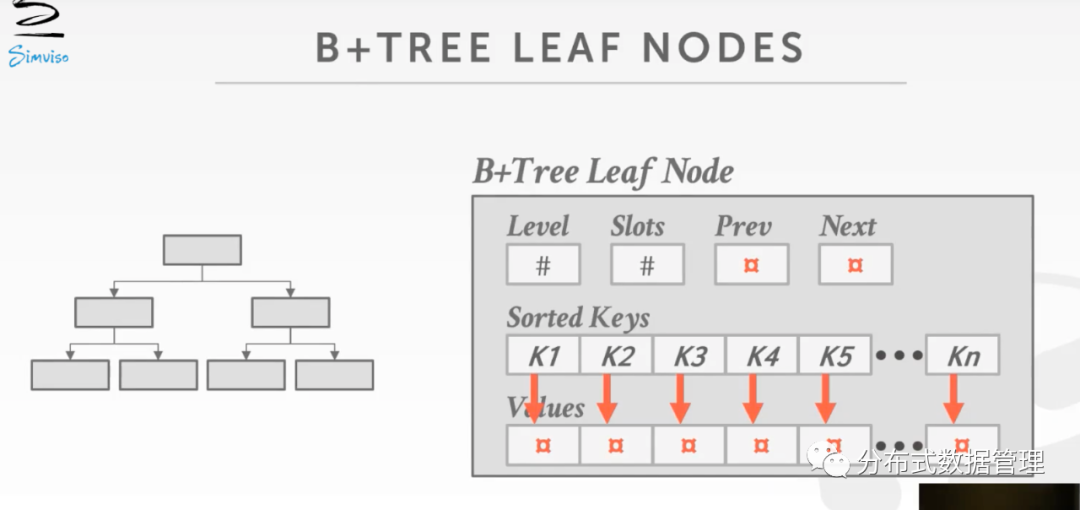
一般教材上都会介绍叶子节点实现如下图,节点中存放一个连续的数组,KEY和VALUE存放在一起,数组的两端的指针指向左右的兄弟节点(或者为NULL,例如在树的一侧时)。
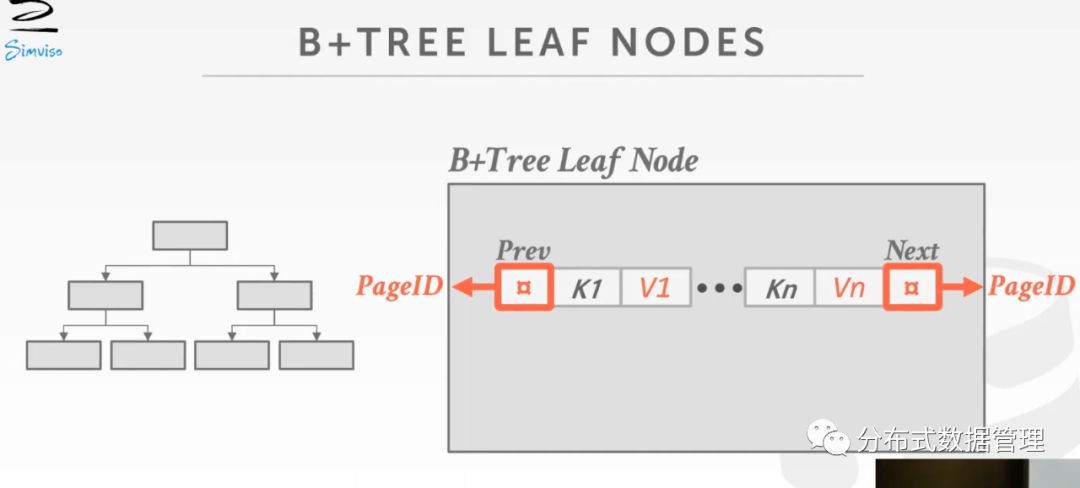
但是实际工程实现时,KEY和VALUE是分开存储的,如图所示,其中,Level字段表示当前节点的深度,Slots表示节点还能存放数据个数,Pre和Next功能和前面的一样:
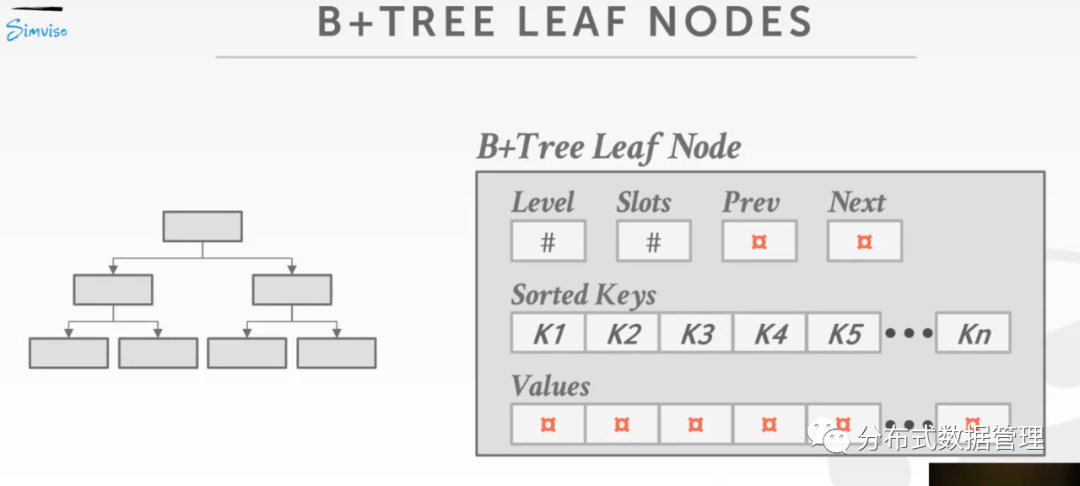
将KEY与VALUE分开存储是因为这两者的字段长度一般不同且KEY一般长度固定VALUE多为变长,为了利用KEY有序的特点进行二分查找,将KEY单独存储可以在二分查找时候方便程序代码跳转,当找到KEY之后再根据相应的Offset获取相应的VALUE。
VALUE可能是Record ID 或者数据 Tuple本身,目前绝大多数商业数据库中B+ 树叶子节点中存放的是Record ID,MySQL用的是第二种。
B Tree VS. B+ Tree
B+ 树中除了叶子节点存放数据外,中间节点也会存放数据但不是真实数据
B 树真实数据存放在中间节点和叶子节点
出于工程实现复杂度,即使B+ 树需要多余存储开销,工程上绝大多数情况使用B+ 树
B Tree Insert
首先根据根节点和中间节点找到在叶节点应该插入的位置,插入数据后判断叶节点是否需要分裂(根据叶子节点中的KEY数目是否达到上限M),分裂后是否需要向上继续递归分裂。
B Tree Delete
一开始的步骤和插入相同,根据根节点和中间节点找到要删除的节点位置,若删除后节点中KEY的数目小于M/2-1(半数),首先尝试将兄弟中某些KEY归到自己节点中,若拉取节点后会导致兄弟节点中的KEY达到不了半数,兄弟节点之间尝试合并。合并后若导致父节点的KEY小于半数,递归之前的过程直到树重新平衡。
B+ Tree in Practice

填充因子
B+ 树的填充因子指的是节点保存的所有数据中有用的部分占总数据的比例。多余的空间是为新数据的预留空间,也能控制页面的分裂和合并。在实际场景中发现,B+ 树的的常用的填充因子在67%到69%,此时节点中保存的数据大约67%是有用的。
标准容量
对于8KB的Page大小,若一个节点占一个Page,如果树的高度是4,填充因子在67%,B+树共可以保存约3,000,000个KEY/VALUE对,对其中任意一个KEY条目的搜索效率都是log(n)。树的第一层8KB,第二层1MB,第3层140MB。
聚簇索引
数据库一张表在磁盘中存放可能是无序的,每当数据库要插入一条新的记录时,记录可能被插入到任何磁盘的任何当前空闲块中。但是为了数据读取性能,我们希望数据在磁盘中能够按某种顺序存储(比如数据可以根据主键顺序存储,像B+树的叶子节点中存实际数据的情况,不只是record ID。因为如果页节点存放的只是Record ID,根据Record ID访问数据时候仍然由于随机读写带来大量I/O),这样读数据的性能将能够提高。
数据库中的聚簇索引(Clustered Index)被用来达到这个目的,聚簇索引会将数据库存在磁盘上的数据按照某个键的顺序重新组织,B/B+树也是这一类索引。
B+ Tree Search
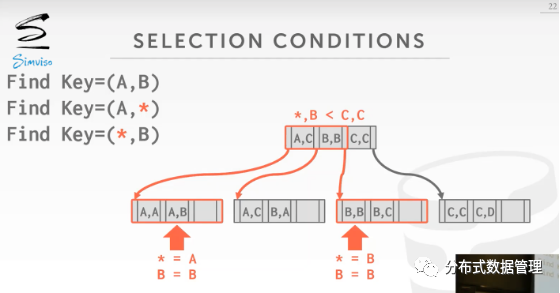
B+树支持在复合KEY上的模糊查询,例如上图索引上查询KEY(*,B),首先从根节点出发,发现(A,C)、(B,B) 和 (C,C)的左子树都可能满足条件,因此它们的这几个指针所指向的节点中的数据都要扫描。Oracle中称之为Skip Scan。
B+ Tree Optimization

工程上针对B+ 树常见的优化有:
节点大小设置

B/B+树的节点大小设置取决于存储介质的读取速度,由于一个节点中的数据都是顺序存储,这样可以增加读取数据的性能。机械硬盘由于读取速度慢,每个页的大小设置为1MB,SSD一般设置为10KB,内存数据库则可以设置为512B即可。也可以根据Workload躯体情况再做调整。
节点合并、拆分时机设置

变长Key处理

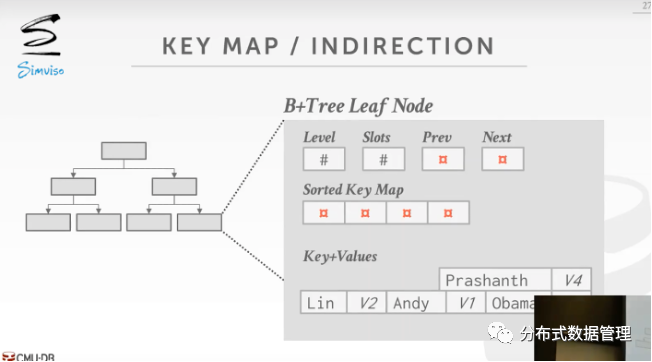
若B+树种存放的Key是变长的,一般有4种方法处理,实际工程中常使用第三种或第四种,第三种方法的填充位会造成浪费空间。第四种方法(key map间接映射)示意图如下:
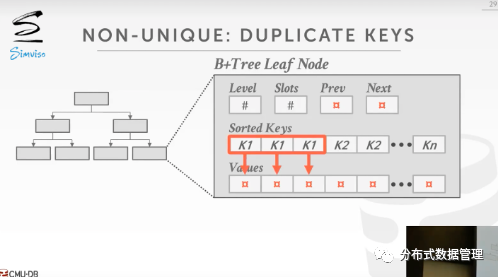
非唯一键的处理方法

这种情况是指当叶子节点中一个Key对应了多个Value时,叶节点中的数据有两种存放策略:
① 复制Key,每个Key指向一个Value
② 每一个Key对应一个Value List 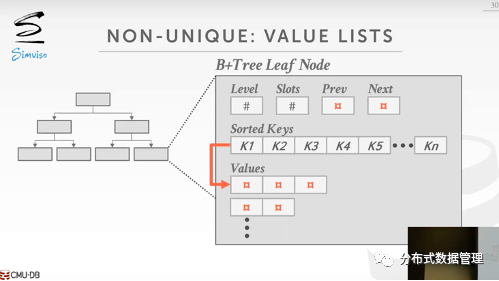
内部节点搜索

在B+树搜索的过程中,经常要将节点中的KEY与要检索的KEY进行比较,判断继续往左子树搜索还是右子树搜索,如何高效的与节点中的KEY进行比较影响B+树的性能。有以下三种比较方法:
1. 线性扫描
2. 二分查找
3. 插值法(利用已知的一些数据统计信息估计数据的offset),例如上面的例子中,若已知节点中共存7个数据,最大值是10,且数据连续顺序存储,那么Key=8的offset可以用图中的计算方法得到。
B+树其他优化策略

前缀压缩
由于节点中的Key排好序,因此会有相同的前缀,将这些前缀压缩存储将降低存储空间

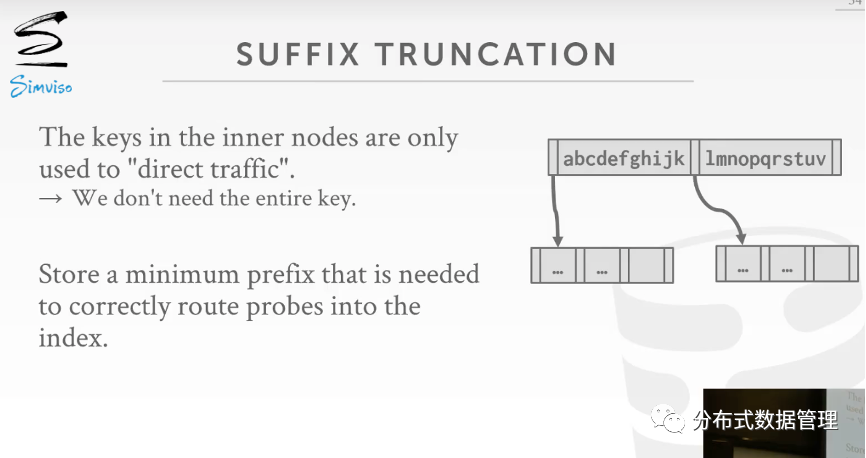
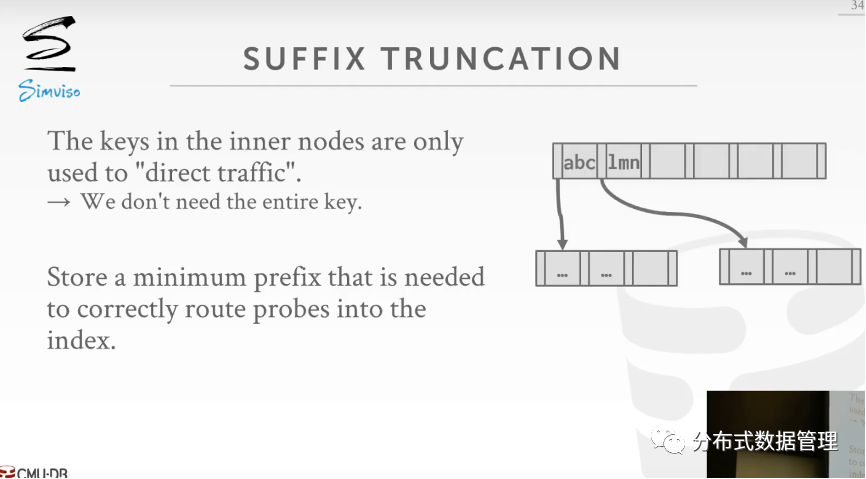
后缀删除
节点中有时仅根据Key前面几个字符就能比较大小了,后面多余的部分可以删除降低存储空间
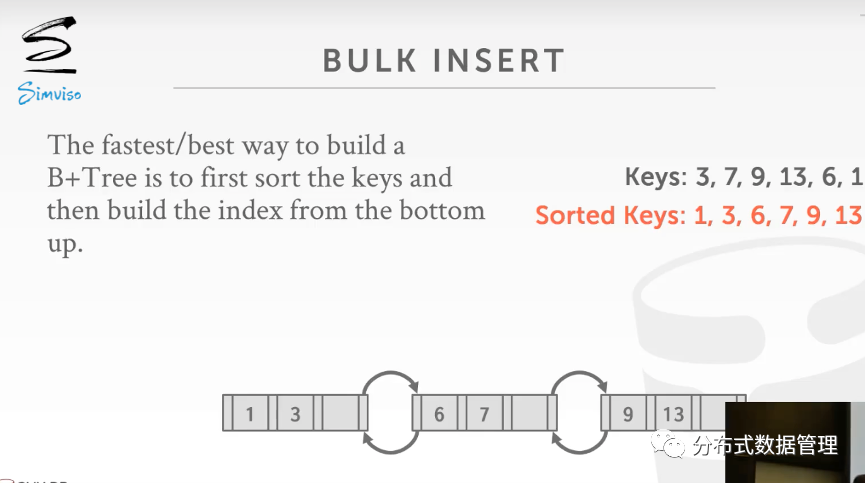
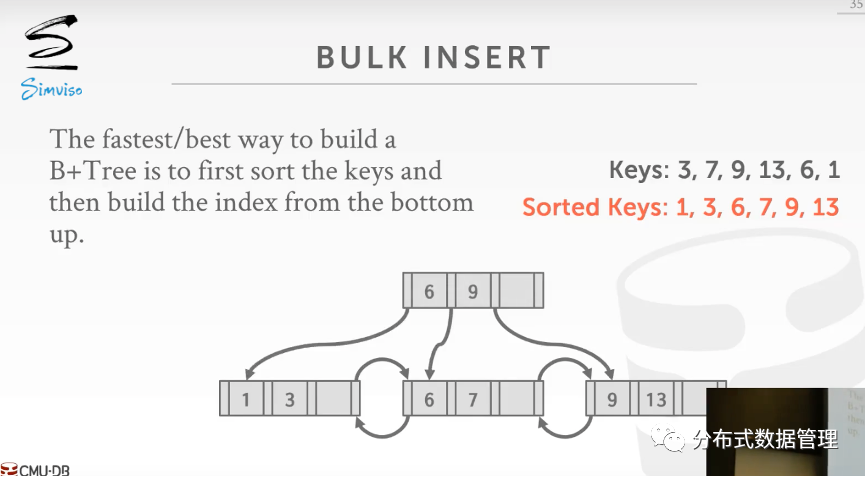
Bulk Insert
在数据初始化阶段,数据批量导入的过程中,不需要立即建立索引,当数据全部导入后再统一建立索引。如下图所示,先对数据排序,然后自底向上建立索引。
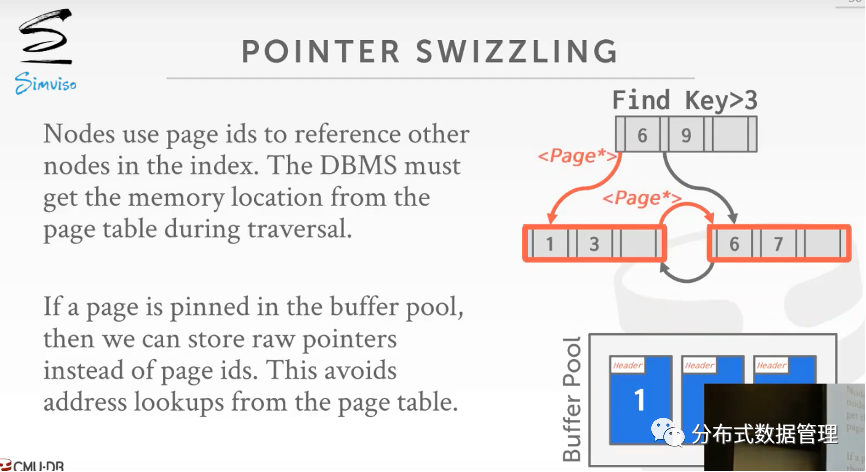
Pointer Swizzling
B+树节点中指向左孩子与右孩子的并非真正地址指针,而是孩子节点所在的的Page ID,由于内存页可能在换进换出后实际地址发生变化,因此需要从Buffer Pool中将Page ID转化为实际地址。
为了减少这一次从Buffer Pool中查询地址的时间开销,B+树使用Pointer Swizzling将节点内存页固定在内存中,不进行换出,这时候只要数据不强制写入磁盘,内存页地址就不会再变化,可以减少进入Buffer Pool的开销。