LeetCode深度优先搜索算法选讲

Code小燕儿 2021-09-01

328

Hello，大家好，本文将以LeetCode算法题为例，为大家介绍深度优先搜索算法，代码语言为C/C++，话不多说，开讲吧！

前言

深度优先搜索（depth-first-search, DFS）是一种用于遍历或搜索树或图的算法；该算法尽可能深的搜索树的分支直到所有的分支都已经被遍历，然后将会回溯到起始节点继续搜索，递归这一过程直到所有的分支节点均被访问，算法终止。

上一段文字显然让人抓狂，下面结合实际的算法题，去一探究竟。

130 被围绕的区域

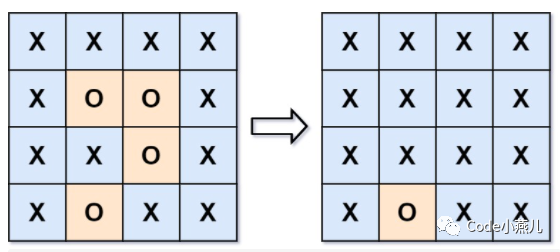
此题为LeetCode算法第130题，示意图如下，要求将所有被'X'包围的'O'同化为'X'。

求解思路：由于矩阵边界处的'O'以及相邻的'O'不会被同化，因此可将这些不被包围的'O'先转化为'A'，之后再遍历矩阵，将其他'O'同化为'X'，将'A'变为'O'，对应C++代码如下:

class Solution {
public:
    void solve(vector<vector<char>>& board) {
        n = board.size();
        m = board[0].size();
        if(m == 0 || n == 0) return;
        // 左右两条边的'O'修改为'A'
        for(int i = 0; i < n; ++i){
            dfs(board, i, 0);
            dfs(board, i, m - 1);
        }
        // 上下两条边的'O'修改为'A'
        for(int j = 1; j < m - 1; ++j){
            dfs(board, 0, j);
            dfs(board, n - 1, j);
        }
        // 将其他'O'变为'X'并还原不被包围的'O'
        for(int i = 0; i < n; ++i){
            for(int j = 0; j < m; ++j){
                if(board[i][j] == 'O') board[i][j] = 'X';
                else if(board[i][j] == 'A') board[i][j] = 'O';
            }
        }
    }
    // 将所有相邻的'O'变为'A'
    void dfs(vector<vector<char>> &board, int i, int j){
        if(i < 0 ||| i >= n || j < 0 || j >= m || board[i][j] != 'O')
            return ;
        board[i][j] = 'A';
        // 上下左右四个方便搜索
        dfs(board, i + 1, j);
        dfs(board, i - 1, j);
        dfs(board, i, j + 1);
        dfs(board, i, j - 1);
    }
private:
    int m, n;
};

对应的C语言代码如下：

void solve(char** board, int boardSize, int* boardColSize){
    if(board == NULL || boardSize == 0) return ;
    for(int i = 0; i < boardSize; ++i){
        if(board[i][0] == 'O'){
            dfs(board, boardSize, boardColSize, i, 0);
        }
        if(board[i][boardColSize[0] - 1] == 'O') {
            dfs(board, boardSize, boardColSize, i, boardColSize[0] - 1);
        }
    }
    for(int j = 0; j < boardColSize[0]; ++j){
        if(board[0][j] == 'O'){
            dfs(board, boardSize, boardColSize, 0, j);
        }
        if(board[boardSize - 1][j] == 'O') {
            dfs(board, boardSize, boardColSize, boardSize - 1, j);
        }
    }
    for(int i = 0; i < boardSize; ++i){
        for(int j = 0; j < boardColSize[0]; ++j){
            if(board[i][j] == 'A') board[i][j] = 'O';
            else if(board[i][j] == 'O') board[i][j] = 'X';
        }
    }
}


void dfs(char **board, int boardSize, int *boardColSize, int i, int j){
    if(i < 0 || i >= boardSize || j < 0 || j >= boardColSize[0] || board[i][j] != 'O')
        return ;
    board[i][j] = 'A';
    dfs(board, boardSize, boardColSize, i + 1, j);
    dfs(board, boardSize, boardColSize, i - 1, j);
    dfs(board, boardSize, boardColSize, i, j + 1);
    dfs(board, boardSize, boardColSize, i, j - 1);
}

79 单词搜索

此题为LeetCode算法第79题，给定一个字符矩阵以及一个单词，要求判断单词是否出现在字符矩阵中，示意图如下

若输入单词为ADE，则返回true，若输入单词为AED，则返回false。

求解思路：遍历字符矩阵，若当前字符为单词首字符，则采用深度优先搜索，为防止重复搜索，我们定义一个visited数组记录字符是否被访问过，C++代码如下：

class Solution {
public:
    bool exist(vector<vector<char>>& board, string word) {
        m = board.size(), n = board[0].size();
        if(m == 0 || n == 0) return false;
        // visited数组记录字符是否被访问
        vector<vector<bool>> visited(m, vector<bool>(n, false));
        for(int i = 0; i < m; ++i){
            for(int j = 0; j < n; ++j){
            // 遇见单词首字符，开始搜索
                if(board[i][j] == word[0]){
                    if(dfs(board, visited, word, i, j, 0)){
                        return true;
                    }
                }
            }
        }
        return false;
    }


    bool dfs(const vector<vector<char>> &board, vector<vector<bool>> &visited, 
            const string &word, int i, int j, int index)
        // 递归退出条件，index到达单词结尾
        if(index == word.size() - 1) return true;
        // 当前字符不同，直接返回
        if(board[i][j] != word[index]) return false;
        // 标记已经被访问过的字符
        visited[i][j] = true;
        // 上下左右四个方向依次搜索
        for(int k = 0; k < 4; ++k){
            int ni = i + dx[k], nj = j + dy[k];
            // 判断条件 1 矩阵索引有效；2 字符未被访问
            // 3 下一index有效；4 下一个word字符与矩阵索引对应字符相等
            if(ni >= 0 && ni < m && nj >= 0 && nj < n && visited[ni][nj] == false 
                && ((index + 1) < word.size()) && board[ni][nj] == word[index + 1]){
                if(dfs(board, visited, word, ni, nj, index + 1)){
                    return true;
                }
            }
        }
        // 回溯
        visited[i][j] = false;
        return false;
    }
private:
    int m, n;
    int dx[4] = {0, 1, 0, -1};
    int dy[4] = {1, 0, -1, 0};
};

C语言版本如下：

bool dfs(char **board, int boardSize, int boardColSize, char *word, int i, int j){
    if(*word == '\0') return true; // 到达单词结尾
    // 数组索引的合法性校验
    if(i < 0 || i >= boardSize || j < 0 || j >= boardColSize || board[i][j] != *word) {
        return false;
    }


    board[i][j] = '\0';
    bool ret = dfs(board, boardSize, boardColSize, word + 1, i + 1, j) ||
               dfs(board, boardSize, boardColSize, word + 1, i - 1, j) ||
               dfs(board, boardSize, boardColSize, word + 1, i, j + 1) ||
               dfs(board, boardSize, boardColSize, word + 1, i, j - 1);


    board[i][j] = *word;
    
    return ret;
}


bool exist(char** board, int boardSize, int* boardColSize, char * word){
    if(!board || boardSize == 0 || !boardSize) return false;
    for(int i = 0; i < boardSize; ++i){
        for(int j = 0; j < *boardColSize; ++j){
            if(board[i][j] == word[0]){
                if(dfs(board, boardSize, *boardColSize, word, i, j)){
                    return true;
                }
            }
        }
    }
    return false;
}

200 岛屿数量

此题为LeetCode算法第200题，给定一个字符矩阵，约定'1'表示陆地，'0'表示水域，求岛屿数量。

思路分析：遍历数组，遇到'1'，则采用DFS搜索，将所有相邻的'1'变为'0'，同时更新岛屿数量count，遍历完成后即可得到结果，C++代码如下：

class Solution {
public:
    int numIslands(vector<vector<char>>& grid) {
        int count = 0;
        row = grid.size(), col = grid[0].size();
        for(int i = 0; i < row; ++i){
            for(int j = 0; j < col; ++j){
                if(grid[i][j] == '1'){
                    dfs(grid, i, j);
                    count ++; // 更新岛屿数量
                }
            }
        }
        return count;
    }


    void dfs(vector<vector<char>>& grid, int i, int j){
        //if(i < 0 || i >= row || j < 0 || j >= col) return;
        grid[i][j] = '0';
        for(int k = 0; k < 4; ++k){
            int ni = i + dx[k], nj = j + dy[k];
            if(ni >= 0 && ni < row && nj >= 0 && nj < col && grid[ni][nj] == '1'){
                dfs(grid, ni, nj);
            }
        }
    }
private:
    int row, col;
    const int dx[4] = {1, 0, -1, 0};
    const int dy[4] = {0, 1, 0, -1};
};

C语言代码如下：

const int dx[4] = {1, 0, -1, 0};
const int dy[4] = {0, 1, 0, -1};


void dfs(char **grid, int gridSize, int gridColSize, int i, int j){
    grid[i][j] = '0';
    if(i + 1 < gridSize && grid[i + 1][j] == '1')
        dfs(grid, gridSize, gridColSize, i + 1, j);
    if(i - 1 >= 0 && grid[i - 1][j] == '1')
        dfs(grid, gridSize, gridColSize, i - 1, j);
    if(j + 1 < gridColSize && grid[i][j + 1] == '1')
        dfs(grid, gridSize, gridColSize, i, j + 1);
    if(j - 1 >= 0 && grid[i][j - 1] == '1')
        dfs(grid, gridSize, gridColSize, i, j - 1);
}


int numIslands(char** grid, int gridSize, int* gridColSize){
    int count = 0;
    for(int i = 0; i < gridSize; ++i){
        for(int j = 0; j < *gridColSize; ++j){
            if(grid[i][j] == '1'){
                dfs(grid, gridSize, *gridColSize, i, j);
                count ++;
            }
        }
    }
    return count;
}

695 岛屿的最大面积

此题为LeetCode算法第695题，与上一题岛屿数量类似，只需要额外定义一个变量记录每个岛屿的面积即可，C++代码如下：

class Solution {
public:
    int maxAreaOfIsland(vector<vector<int>>& grid) {
        row = grid.size();
        col = grid[0].size();
        if(row == 0 || col == 0) return 0;
        for(int i = 0; i < row; ++i){
            for(int j = 0; j < col; ++j){
                if(grid[i][j] == 1){ // 遇见岛屿
                    isLandArea = 0;
                    dfs(grid, i, j); // 求岛屿面积
                    // 更新最大岛屿面积
                    maxArea = max(maxArea, isLandArea);
                }
            }
        }
        return maxArea;
    }


    void dfs(vector<vector<int>> &grid, int i, int j){
        if(!isValid(i, j) || grid[i][j] == 0) return ;
        grid[i][j] = 0; // 将搜索过的陆地标记为水域，防止重复搜索
        isLandArea ++;
        dfs(grid, i + 1, j);
        dfs(grid, i - 1, j);
        dfs(grid, i, j + 1);
        dfs(grid, i, j - 1);
        return;
    }


    bool isValid(int i, int j){
        return (i >= 0) && (i < row) && (j >= 0) && (j < col);
    }
private:
    int maxArea = 0;
    int isLandArea = 0;
    int row, col;
};

C语言代码如下：

int maxArea = 0;
int isLandArea = 0;


void dfs(int **grid, int gridSize, int *gridColSize, int i, int j){
    if(i < 0 || i >= gridSize || j < 0 || j >= *gridColSize || grid[i][j] == 0){
        return ;
    }
    grid[i][j] = 0;
    isLandArea ++;
    dfs(grid, gridSize, gridColSize, i + 1, j);
    dfs(grid, gridSize, gridColSize, i - 1, j);
    dfs(grid, gridSize, gridColSize, i, j + 1);
    dfs(grid, gridSize, gridColSize, i, j - 1);
    return ;
}


int maxAreaOfIsland(int** grid, int gridSize, int* gridColSize){
    if(gridSize == 0 && *gridColSize == 0) return 0;
    for(int i = 0; i < gridSize; ++i){
        for(int j = 0; j < *gridColSize; ++j){
            if(grid[i][j] == 1){
                isLandArea = 0; // 每次都重置岛屿面积
                dfs(grid, gridSize, gridColSize, i, j);
                maxArea = maxArea > isLandArea ? maxArea : isLandArea;
            }
        }
    }


    return maxArea;
}

17 电话号码的数字组合

此题为LeetCode算法第17题，模拟九键输入法，示意图如下：

若输入"56"，则输出{"jm","jn","jo","km","kn","ko","lm","ln","lo"}；

思路分析：此题构建哈希表，然后依次将字母组合即可，C++代码如下：

class Solution {
public:
    vector<string> letterCombinations(string digits) {
        if(digits.empty()) return {};
        dfs(digits, 0);
        return ret;
    }


    void dfs(string &digits, int index){
        if(index == digits.size()) { // 更新结果
            ret.push_back(word);
            return;
        }
        // 遍历数字对应的字符串，依次加入结果即可
        string temp = MAP.at(digits[index]);
        for(int i = 0; i < temp.size(); ++i){
            word += temp[i];
            dfs(digits, index + 1);
            word.pop_back();
        }
    }


private:
    const unordered_map<char,string> MAP =
    {{'2',"abc"},{'3',"def"},{'4',"ghi"},
    {'5',"jkl"},{'6',"mno"},{'7',"pqrs"},
    {'8',"tuv"},{'9',"wxyz"}};


    vector<string> ret;
    string word;
};

C语言代码如下：

char phoneMap[9][5] = {"", "abc", "def", "ghi", "jkl", "mno", "pqrs", "tuv", "wxyz" };


void dfs(char* digits, int digitSize, int index, char* item, int itemSize, char** ans, int* ansSize) {
    if (index == digitSize) {
        // 为结果数组开辟空间
        ans[*ansSize] = (char* )malloc((itemSize + 1) * sizeof(char)); // 为每一个 item 分配独立空间
        strcpy(ans[*ansSize], item);
        (*ansSize)++;
    } else {
        // '1'没有对应的字符串
        char* letters = phoneMap[digits[index] - '1'];
        int size = strlen(letters);
        for (int i = 0; i < size; i++) {
            item[itemSize++] = letters[i];
            item[itemSize] = 0;
            dfs(digits, digitSize, index + 1, item, itemSize, ans, ansSize);
            item[--itemSize] = 0;
        }
    }
}
char** letterCombinations(char* digits, int* returnSize) {
    int digitSize = strlen(digits);
    *returnSize = 0;
    if (digitSize == 0) {
        return NULL;
    }
    // 开辟堆空间
    int num = pow(4, digitSize);
    char** ans = (char**)malloc(num * sizeof(char*));
    char* item= malloc((digitSize + 1) * sizeof(char));
    dfs(digits, digitSize, 0, item, 0, ans, returnSize);
    return ans;
}

491 递增子序列

此题为LeetCode算法第491题，给定一个数字数组，输出所有的递增子序列，例如输入数组为[5, 3, 7, 7]，则输出结果为[[5, 7], [5, 7, 7], [3, 7], [3, 7, 7], [7, 7]]；

解题思路：遍历数组，若当前数组元素nums[index]比基准元素cur大，则将nums[index]加入到结果数组item中，更新cur为nums[index]，继续下一趟遍历；若nums[index]与cur不等，则cur不更新，继续下一趟遍历，C++代码如下：

class Solution{
public:
    vector<vector<int>> findSubsequences(vector<int> &nums){
        dfs(nums, 0, INT_MIN);
        return res;
    }
    
    void dfs(vector<int> &nums, int index, int cur){
        if(idnex == nums.size()){ // 更新结果数组
            if(item.size() > 1){
                res.push_back(item);
            }
            return ;
        }
        // 当前数值nums[index]大于基准数字
        // 将基准数字更新为当前数字nums[index]，继续下一轮遍历
        // 当前： [2, 3, 5] cur = 2, nums[index] = 3;
        // 下一轮： [2, 3, 5] cur = 3, nums[index+1] = 5
        if(nums[index] >= cur){
            item.push_back(nums[index]);
            dfs(nums, index + 1, nums[index]);
            item.pop_back();
        }
        // 当前数值nums[index]不等于基准数字
        // 基准数字不更新，继续下一轮遍历
        // 当前： [4, 3, 5] cur = 4, nums[index] = 3;
        // 下一轮： [4, 3, 5] cur = 4, nums[index + 1] = 5;
        if(nums[index] != cur){
            dfs(nums, index + 1, cur);
        }
        return ;
    }
private:
    vector<vector<int>> res;
    vector<int> item;
}

C语言代码如下：

int **res;
int *item;
int itemSize, resSize;


void dfs(int *nums, int numsSize, int index, int cur, int **returnColumnSizes){
    if(index == numSize){
        if(itemSize > 1){
            res[resSize] = (int*)malloc(sizeof(int) * itemSize);
            memcpy(res[resSize], item, sizeof(int) * itemSize);
            (*returnColumnSizes)[resSize ++] = itemSize;
        }
        return ;
    }
    if(nuns[index] >= cur){
        item[itemSize ++] = nums[idnex];
        dfs(nums, numsSize, index + 1, nums[index], returnColumnSizes);
        itemSize--;
    }
    if(nums[index] != cur){
        dfs(nums, numsSize, index + 1, cur, returnColumnSizes);
    }
    return ;
}


int **findSubsequences(int *nums, int numsSize, int *returnSize, int **returnColumnSizes){
    res = (int **)malloc(sizeof(int *) * 32767);
    (*returnColumnSizes) = (int **)malloc(sizeof(int *) * 32767);
    item = (int *)malloc(sizeof(int) * numsSize);
    resSize = itemSize = 0;
    dfs(nums, numsSize, 0, INT_MIN, returnColumnSizes);
    *returnSize =  resSize;
    return res;
}

329 矩阵中的最长递增路径

此题为LeetCode算法第329题，给定矩阵，求最长递增路径的长度，示意图如下：

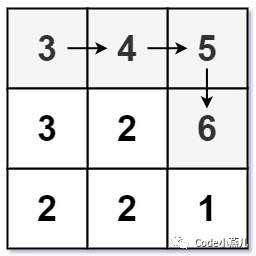
则该矩阵的最长递增路径长度为4。

求解思路：采用记忆化深度优先搜索，定义矩阵memo，其中memo[i][j]表示以输入矩阵元素matrix[i][j]为起点的最长递增路径长度，在遍历数据搜索时，若memo[i][j]不为零，则可直接读取缓存结果；若memo[i][j]为零，则需要进行搜索并得到最大值；C++代码如下：

class Solution{
public:
    int longestIncreasingPath(vector<vector<int>> &matrix){
        row = matrix.size(), col = matrix[0].size();
        if(row == 0 || col == 0) return 0;
        for(int i = 0; i < row; ++i){
            for(int j = 0; j < col; ++j){
                if(memo[i][j] == 0){ // 当前节点未访问
                    res = max(res, dfs(matrix, i, j, memo);
                }
            }
        }
        return res;
    }
    
    int dfs(vector<vector<int>> &matrix, int i, int j, vector<vector<int>> &memo){
        if(memo[i][j]) return memo[i][j]; // 当前节点已经访问过
        ++memo[i][j];
        for(int k = 0; k < 4; ++k){
            int ni = i + dx[k], nj = j + dy[k];
            // matrix[ni][nj] > matrix[i][j] 可减少搜索次数
            if(isValid(i, j) && matrix[ni][nj] > matrix[i][j]){
                memo[i][j] = max(memo[i][j], 1 + dfs(matrix, ni, nj, memo));
            }
        }
        return memo[i][j];
    }
private:
    int row, col;
    int res = 1;
    const int dx[4] = {1, 0, -1, 0};
    const int dy[4] = {0, 1, 0, -1};
}

C语言代码如下：



const int dx[4] = {1, 0, -1, 0};
const int dy[4] = {0, 1, 0, -1};


bool isValid(int i, int j, int matrixSize, int matrixColSize){
    return (i >= 0) && (i < matrixSize) && (j >= 0) && (j < matrixColSize);
}


int dfs(int **matrix, int matrixSize, int *matrixColSize, int i, int j, int **memo){
    if(memo[i][j]) return memo[i][j];
    ++memo[i][j];
    for(int k = 0; k < 4; ++k){
        int ni = i + dx[k], nj = j + dy[k];
        if(isValid(ni, nj, matrixSize, *matrixColSize) && matrix[ni][nj] > matrix[i][j]){
            int temp = dfs(matrix, matrixSize, matrixColSize, ni, nj, memo) + 1;
            memo[i][j] = memo[i][j] > temp ? memo[i][j] : temp;
        }
    }
    return memo[i][j];
}


int longestIncreasingPath(int** matrix, int matrixSize, int* matrixColSize){
    if(matrix == NULL) return 0;
    int **memo = (int **)malloc(sizeof(int *) * matrixSize);
    for(int i = 0; i < matrixSize; ++i){
        memo[i] = (int *)calloc(*matrixColSize, sizeof(int));
    }
    int res = 0;
    for(int i = 0; i < matrixSize; ++i){
        for(int j = 0; j < *matrixColSize; ++j){
            if(memo[i][j] == 0){
                int cur = dfs(matrix, matrixSize, matrixColSize, i, j, memo);
                res = res > cur ? res : cur;
            }
        }
    }
    for(int i = 0; i < matrixSize; ++i){
        free(memo[i]);
    }
    free(memo);
    return res;
}

后记

本文选取了几个典型的深度优先搜索算法题进行讲解，总的代码框架如下

void dfs(int step){
    // 边界判断 递归出口
    // 遍历每一种可能
    for(;;){
        // 去重剪枝优化时间复杂度
        dfs(step + 1); // 递归
    }
}

当时在实际做题的过程中，不同的算法题存在诸多变化，这就需要我们多多刷题提高代码量，认真总结经验提升代码效率。

本文内容到此结束啦，欢迎大家点赞收藏在看，欢迎大家勘误或提出有效的建议(seuhyz@163.com)，谢谢大家的支持。

数据库

文章转载自Code小燕儿，如果涉嫌侵权，请发送邮件至：contact@modb.pro进行举报，并提供相关证据，一经查实，墨天轮将立刻删除相关内容。

LeetCode深度优先搜索算法选讲

评论