题目描述（Hard）

给你一个整数数组 nums ，返回 nums 中所有 等差子序列 的数目。

如果一个序列中 至少有三个元素 ，并且任意两个相邻元素之差相同，则称该序列为等差序列。

• 例如，[1, 3, 5, 7, 9]、[7, 7, 7, 7] 和 [3, -1, -5, -9] 都是等差序列。
• 再例如，[1, 1, 2, 5, 7] 不是等差序列。

数组中的子序列是从数组中删除一些元素（也可能不删除）得到的一个序列。

• 例如，[2,5,10] 是 [1,2,1,2,4,1,5,10] 的一个子序列。

题目数据保证答案是一个 32-bit 整数。

示例 1：

输入：nums = [2,4,6,8,10] 输出：7 解释：所有的等差子序列为：[2,4,6] [4,6,8] [6,8,10] [2,4,6,8] [4,6,8,10] [2,4,6,8,10] [2,6,10]

示例 2：

输入：nums = [7,7,7,7,7] 输出：16 解释：数组中的任意子序列都是等差子序列。

提示：

• 1  <= nums.length <= 1000
• -2^31 <= nums[i] <= 2^31 - 1

链接：https://leetcode-cn.com/problems/arithmetic-slices-ii-subsequence

方法一在于对官方题解的理解，方法二更美妙，不想理解官方题解的，可以直接下拉到方法二。

题目理解

今天这题是在昨天题目基础上的加强版，昨天的题目是要求子数组，今天的要求是子序列，子数组在原数组中是连续的，而子序列可以不用连续，只要保证相对顺序不变即可。

昨日题解快速入口：413. 等差数列划分。

让我们简单回顾一下昨天的解法，比如，给定数组为[1,2,3,4,5]，求等差子数组，我们使用动态规划的过程，一次遍历：

• 遍历到3，发现它跟[1,2]可以组成子数组[1,2,3]，满足等差子数组要求，记dp[3]=1
  。
• 遍历到4，发现它跟[2,3]可以组成子数组[2,3,4]，满足等差子数组要求，而它的前一位即3本来就有一个等差子数组，我们在它的基础上可以延续出来一个新的等差子数组[1,2,3,4]，所以，dp[4]=dp[3]+1=2
  ，dp[3]表示原来3的基础上延续出来的[1,2,3,4]，+1表示全新的[2,3,4]。
• 遍历到5，发现它跟[3,4]可以组成子数组[3,4,5]，满足等差子数组要求，而它的前一位即4本来是有两个等差子数组，我们在它的基础上可以延续出来两个新的等差子数组分别为[1,2,3,4,5]和[2,3,4,5]，所以，dp[5]=dp[4]+1=3
  ，解释同上。

这样，我们把dp[3]+dp[4]+dp[5]=1+2+3=6
就是答案。

方法一、动态规划

好了，今天的题目是要求等差子序列，还是以[1,2,3,4,5]为例，[1,3,5]也是一个合格的答案，所以，我们可以转换成昨天的题目，我们求出每一个以nums[i]结尾的公差d的元素个数，再按照上述求等差子数组的思路很容易求出以nums[i]结尾等着为d的等差子数组的数量，把所有这些等差d加一起就是以nums[i]结尾的等差子序列的数量，列举所有的i即可求得结果，所以，我们定义如下：

状态定义：dp[i][d]
表示以nums[i]结尾，公差为d的等差子数组的数量。

状态转移：dp[i][d]=dp[j][d]+1
，其中j表示以nums[i]结尾等着为d的前面那个数nums[j]的下标。

这样定义看似没有问题，实际运行的过程其实是有问题的：

• 问题一：以[1,2,3,4,5]为例，遍历到2（下标为1）的时候，它与下标0的元素1的差值为1，按照公式应该得到：dp[1][1]=dp[0][1]+1=1
  ,但是这个结果并不符合题目的要求，题目要求长度至少为3，那么，我们怎么才能知道下标j前面还有没有元素呢？如果只有[nums[j], nums[i]]是无法满足长度3的要求的。
• 问题二：以[7,7,7,7,7]为例，遍历到第4个7（下标为3）的时候，它的等差子序列有4个，分别为[7(0),7(1),7(3)]
  、[7(0),7(2),7(3)]
  、[7(1),7(2),7(3)]
  、[7(0),7(1),7(2),7(3)]
  ，按照dp[i][d]=dp[j][d]+1
  的规则去计算也是不对的。

似乎没有思路了。再仔细想一下，既然三个长度的子序列是由两个长度的子序列升级来的，那么，我们能不能在统计结果的时候从两个长度的子序列开始计算呢，这样，三个长度的子序列就不用计算了。比如，以[1,2,3,4,5]为例：

• 遍历到2时，以2结尾的子序列只有一个，即[1,2]，我们记为dp[2][1]=1
  。
• 遍历到3时，以3结尾的子序列有三个，分别为[1,2,3]、[1,3]、[2,3]，我们分别记为dp[3][1]=dp[2][1]+1=2
  和dp[3][2]=dp[1][2]+1=1
  ，可以看到，只有dp[2][1]
  升级上来的那个子序列才可以作为结果，所以，我们在这里ans += dp[2][1]
  。
• 遍历到4时，以4结尾的子序列有多少个呢？它与前面元素的公差分别有1、2、3，我们按照公式可得dp[4][1]=dp[3][1]+1=3
  、dp[4][2]=dp[2][2]+1=1
  、dp[4][3]=dp[1][3]+1=1
  ，一共五个，分别是[1,4]
  、[2,4]
  、[3,4]
  、[2,3,4]
  、[1,2,3,4]
  ，可以看到，只有dp[3][1]
  升级上来的那两个子序列才满足条件，所以，ans += dp[3][1]
  。

再来看看[7,7,7,7,7]这种特殊用例，遍历到第4个7的时候，它与前面任意元素的差值都是0，按照前面的公式dp[i][0]=dp[j][0]+1
就不行了，这时候我们可以换成累加就可以轻松解决了，dp[i][0]+=dp[j][0]+1
。

最后，题目限定nums[i]的范围为-2^31 <= nums[i] <= 2^31 - 1
，有可能溢出，而且，我们也不知道等差d有多少个，所以，使用HashMap来存储key为公差的等差子数组数量。

好了，上代码：

class Solution {
    public int numberOfArithmeticSlices(int[] nums) {
        int n = nums.length;
        if (n < 3) {
            return 0;
        }

        int ans = 0;

        // 数组下标i与nums下标i一致，key表示每个等差d
        // 可以看成是等于dp[n][d]
        Map<Long, Integer>[] dp = new Map[n];

        for (int i = 0; i < n; i++) {
            dp[i] = new HashMap<>();
            for (int j = 0; j < i; j++) {
                // 求差值d
                long d = 1L*nums[i] - nums[j]; // 注意可能溢出
                // dp[j][d]的结果
                int cnt = dp[j].getOrDefault(d, 0);
                // 结果为前面所有的长度大于等于2的子序列之和
                ans += cnt;
                // 计算dp[i][d]，可以看成dp[i][d]+=dp[j][d]+1
                dp[i].put(d, dp[i].getOrDefault(d, 0) + cnt + 1);
            }
        }

        return ans;
    }
}

• 时间复杂度：O(n^2)，双层循环。
• 空间复杂度：O(n^2)，dp数组一维需要n的长度，二维取决于d的数量，但不会超过n。

运行结果如下：

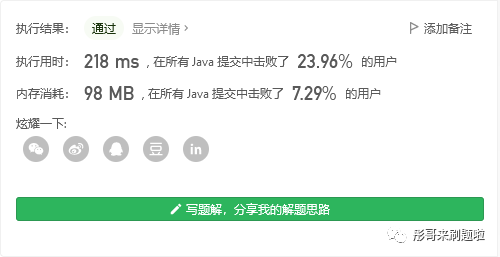
吐血了，这么慢！

方法二、依然动态规划

考虑到方法一那么慢，我们换一种思路。

方法一的二维使用的公差d，而这个d的值有可能很大，所以，使用map来存储，使用map本身就是会增加时间的，那么，我们不存储d行不行呢？

其实也是可以的，我们就把最后两个元素一起存储下来就得了，请看动态规划方程：

• 状态定义：dp[j][i]
  表示以[..,nums[j],nums[i]]
  为结尾的等差子序列的数量；
• 状态转移：dp[j][i]=∑(dp[k][j]+1)
  ，∑为求和符号，我们只要找到所有满足条件的k，就可以组成[..,nums[k],nums[j],nums[i]]
  的子序列，这里我们使用Map+List存储所有元素对应的下标，这样很方便就能找到这样的k了。

请看代码，加了详细注释：

class Solution {
    public int numberOfArithmeticSlices(int[] nums) {
        int n = nums.length;
        if (n < 3) {
            return 0;
        }

        // 记录所有元素的下标，有可能有重复元素，所以，使用list
        Map<Integer, List<Integer>> map = new HashMap<>();
        for (int i = 0; i < n; i++) {
            List<Integer> list = map.getOrDefault(nums[i], new ArrayList<>());
            list.add(i);
            map.put(nums[i], list);
        }

        int ans = 0;

        // dp[j][i]表示以[nums[j],nums[i]]结尾的子序列的等差子序列数量
        // 这里我们可以识别到只统计长度大于等于3的子序列
        int[][] dp = new int[n][n];
        for (int i = 1; i < n; i++) {
            for (int j = 0; j < i; j++) {
                // 看能不能找到nums[k]使得 nums[i]-nums[j]=nums[j]-nums[k]
                // =====>  nums[k] = 2 * nums[j] - nums[i]
                long numsK = 2L * nums[j] - nums[i];
                if (numsK > Integer.MAX_VALUE || numsK < Integer.MIN_VALUE) {
                    continue;
                }

                // 能找到这样的k，说明可以缓存三元组，找不到说明不会组成三元组
                // 正好题目要求的也是最低长度为3
                if (map.containsKey((int)numsK)) {
                    List<Integer> list = map.get((int) numsK);
                    for (Integer k : list) {
                        if (k < j) {
                            // 如果有多个k，需要累加，比如[7,7,7,7,7]这种用例
                            dp[j][i] += dp[k][j] + 1;
                        }
                    }
                }

                ans += dp[j][i];
            }
        }

        return ans;
    }
}

• 时间复杂度：O(n^2)，两层循环。
• 空间复杂度：O(n^2)，map空间复杂度为O(n)，dp数组空间复杂度为O(n^2)。

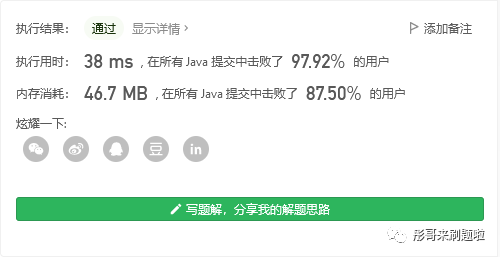
运行结果如下，比方法一好很多，也好理解：

最后

如果对你有帮助，请点个赞吧，谢谢^^

也可以关注我的公号【彤哥来刷题啦】，每日分享题解，一起刷题，一起拿全家桶。