【基础】彻底用图解教会你——中缀表达式转后缀和前缀

编程新说 2021-09-03

2965

强制刷新你的记忆

中缀表达式，大家最熟悉了。就是运算符在操作数中间。像这样：

1 + 2 * 3 + 4

它的特点是：

运算符和操作数必须依次间隔出现，不允许两个操作数中间没有运算符，也不允许两个运算符中间没有操作数。

备注：一元运算符等特殊情况除外。

如果要改变表达式的计算顺序，只有一种方法，加括号，像这样：

(1 + 2) * (3 + 4)

括号的本质：

括号其实是提高了括号里面运算符的优先级，而且括号嵌套的层次越多，它里面的运算符的优先级提高的就越多。

中缀和括号的优点：

非常直观，特别适合人类理解。

中缀和括号的缺点：

不够纯粹，毕竟括号和普通运算符是不一样的。还有就是计算机无法直接计算。

于是一个波兰的数学家就想办法把括号去掉了，就是下面这个。

前缀表达式，运算符写在前面，操作数写在后面，像这样：

* + 1 2 + 3 4

这就是上面那个带括号的对应的前缀形式，可以看到括号已经没有了。

它的特点是：

以运算符开头，以操作数结尾，除此之外没有什么特点，且一眼看上去根本看不出对错，多个运算符可以挨在一起，多个操作数也可以挨在一起。特别是初学者，一定要记住这些，不要受中缀的影响。

大家为了纪念这哥们儿，也称这种形式为“波兰式”。

不得不说，人类还是很善于思考的，既然运算符在操作数前面是可以的，那么倒过来是不是也可以啊？

后缀表达式，操作数写在前面，运算符写在后面，像这样：

1 2 + 3 4 + *

这就是上面那个带括号的对应的后缀形式，可以看到括号也已经没有了。

它的特点是：

以操作数开头，以运算符结尾，然后就和前缀是一样的，一眼看不出对错，运算符可以挨着，操作数可以挨着，这里再次提醒初学者，要记住这些特点。

由于这种形式和“波兰式”正好相反，因此也称为“逆波兰式”。

后缀式和前缀式的计算过程

表达式的计算要用到栈，所以先准备两个栈，一个用红色标记，一个用绿色标记。

后缀式的计算过程，先看动画，再看分步解析：

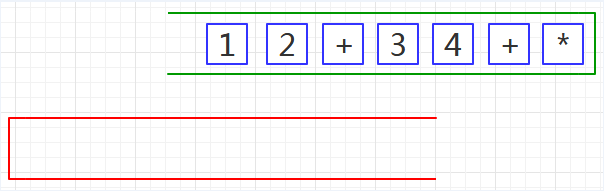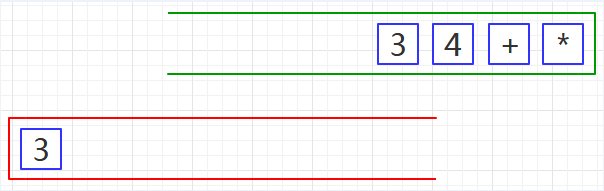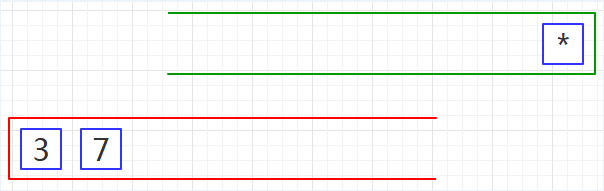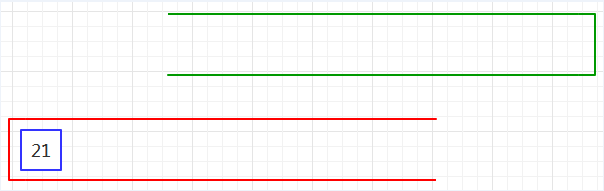
第一步、把后缀表达式装入绿栈，使表达式的头部位于栈顶，如下图01：

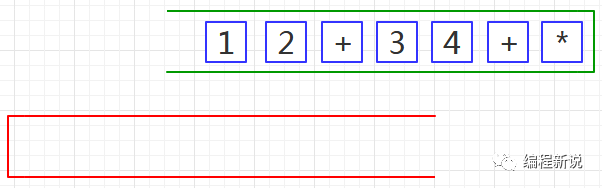
第二步、从绿栈中弹出元素并压入红栈，直至遇到运算符为止，如下图02：

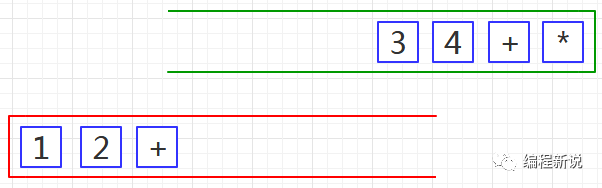
第三步、将红栈中的运算符及其后的两个操作数弹出，计算出结果后并再次压入红栈，如下图03：

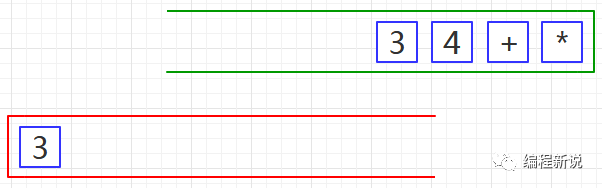
第四步、重复第二步，如下图04：

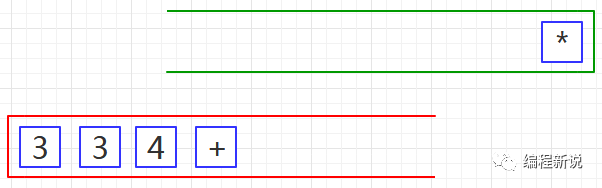
第五步、重复第三步，如下图05：

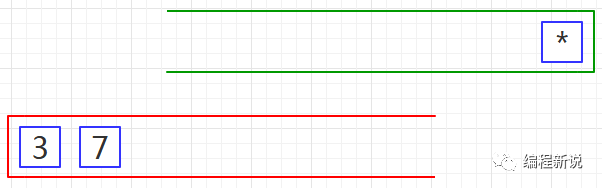
第六步、重复第二步，如下图06：

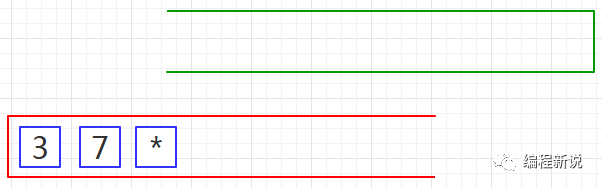
第七步、重复第三步，如下图07：

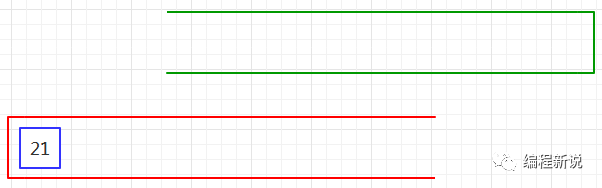
第八步、绿栈已空，表达式计算完毕，红栈中的元素便是表达式的结果。

前缀式的计算过程，先看动画，再看分步解析：

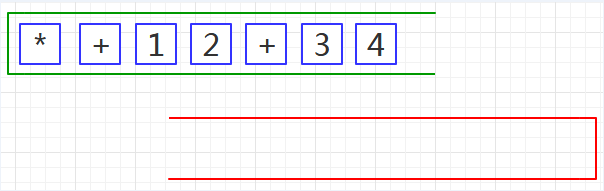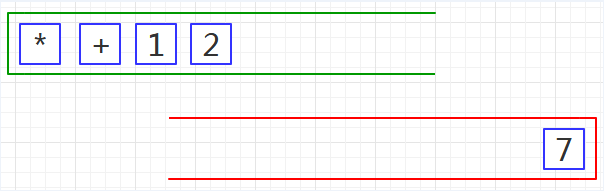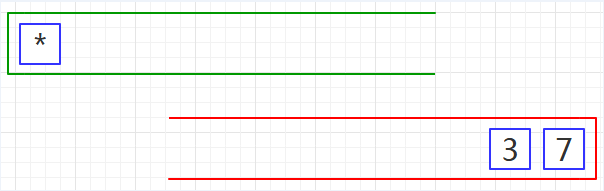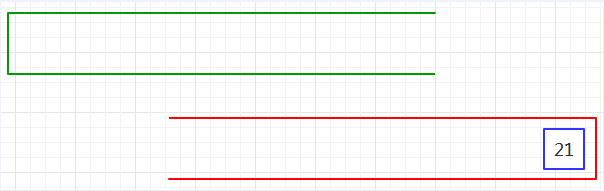
第一步、把前缀表达式装入绿栈，使表达式的尾部位于栈顶，如下图08：

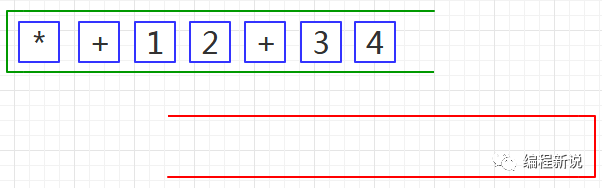
第二步、从绿栈中弹出元素并压入红栈，直至遇到运算符，如下图09：

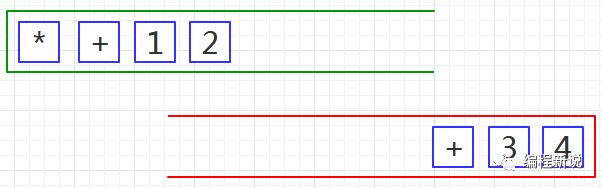
第三步、将红栈中的运算符及其后的两个操作数弹出，计算出结果后并再次压入红栈，如下图10：

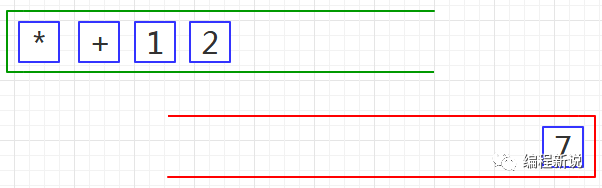
第四步、重复第二步，如下图11：

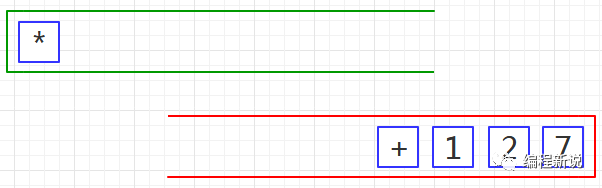
第五步、重复第三步，如下图12：

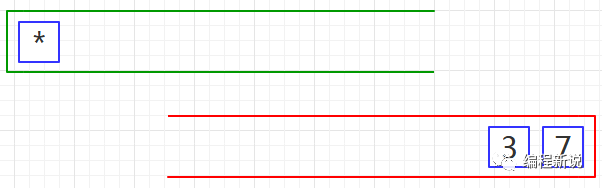
第六步、重复第二步，如下图13：

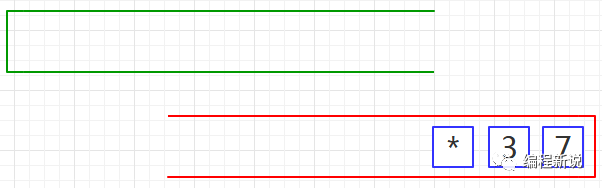
第七步、重复第三步，如下图14：

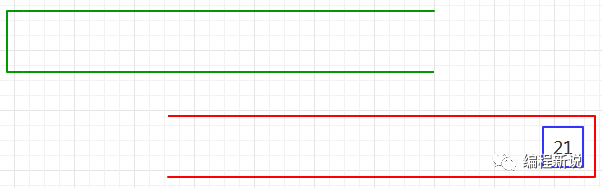
第八步、绿栈已空，表达式计算完毕，红栈中的元素便是表达式的结果。

可以看到，前缀表达式和后缀表达式的计算逻辑完全相同，而且非常的简单，这得益于前、后缀表达式的结构良好。

那么问题来了，如何将中缀表达式转化为前、后缀表达式呢？

中缀表达式转换为后缀表达式

表达式的转换要用到TokenReader和栈，TokenReader用来读取中缀表达式，一次读取一个Token。再准备两个栈，一个用红色标记，一个用绿色标记。

中缀转后缀，先看视频，再看分步解析：

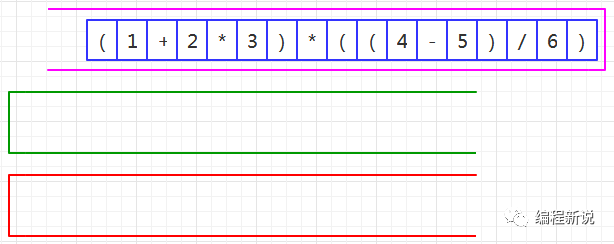
第一步、把中缀表达式装入TokenReader，并准备好从头部开始读取，如图15：

第二步、读取到左括号，压入绿栈，如图16：

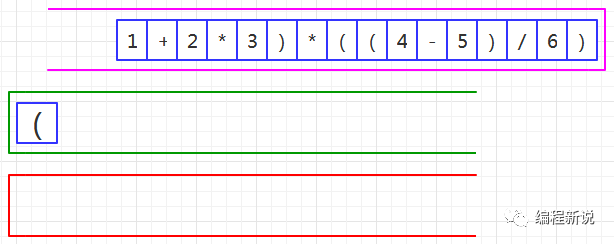
第三步、读取到操作数，压入红栈，如图17：

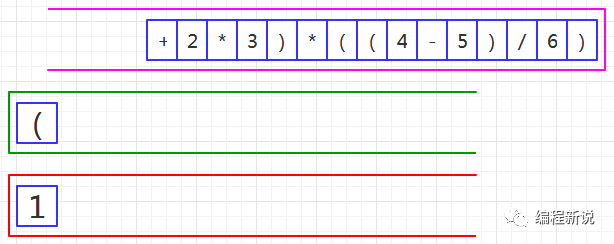
第四步、读取到加号，由于绿栈栈顶是左括号，所以压入绿栈，如图18：

第五步、读取到操作数，压入红栈，如图19：

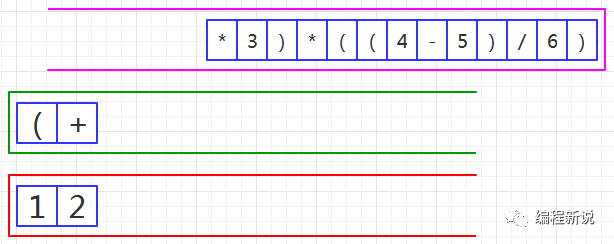
第六步、读取到乘号，由于绿栈栈顶是加号，优先级低，所以压入绿栈，如图20：

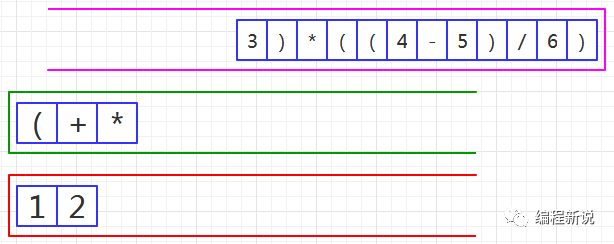
第七步、读取到操作数，压入红栈，如图21：

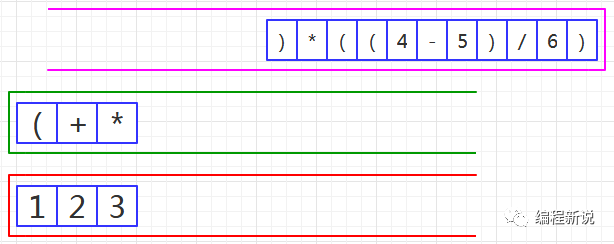
第八步、读取到右括号，绿栈中运算符依次弹出并压入红栈，直至遇到左括号为止，如图22：

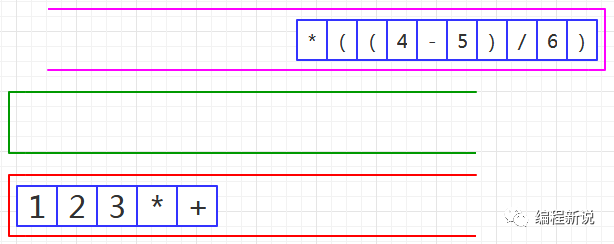
第九步、读取到乘号，压入绿栈，如图23：

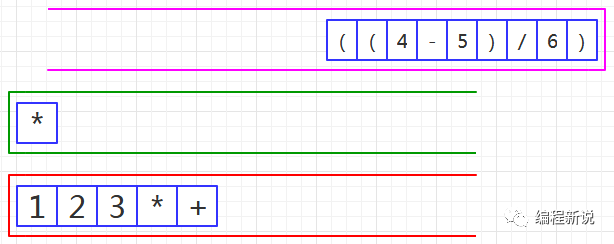
第十步、读取到左括号，压入绿栈，如图24：

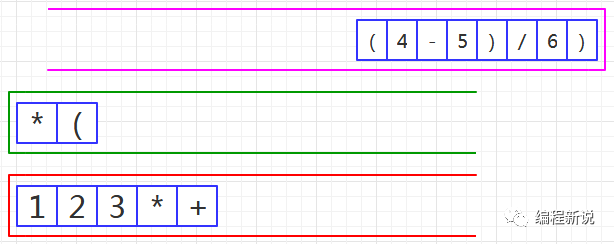
第十一步、读取到左括号，压入绿栈，如图25：

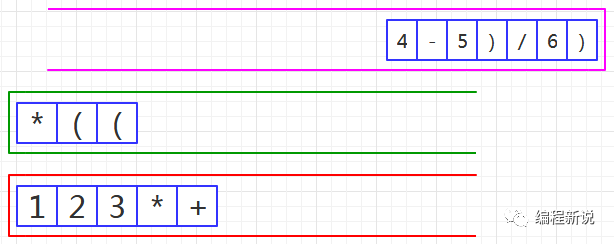
第十二步、读取到操作数，压入红栈，如图26：

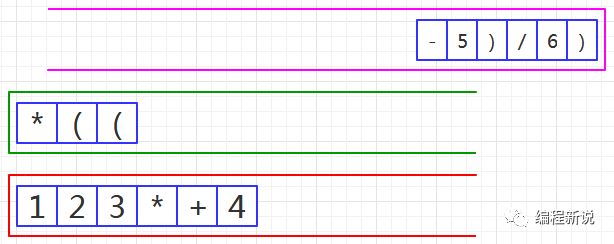
第十三步、读取到减号，由于绿栈栈顶是左括号，所以压入绿栈，如图27：

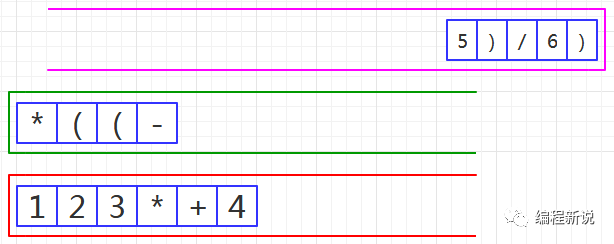
第十四步、读取到操作数，压入红栈，如图28：

第十五步、读取到右括号，绿栈中运算符依次弹出并压入红栈，直至遇到左括号为止，如图29：

第十六步、读取到除号，由于绿栈栈顶是左括号，所以压入绿栈，如图30：

第十七步、读取到操作数，压入红栈，如图31：

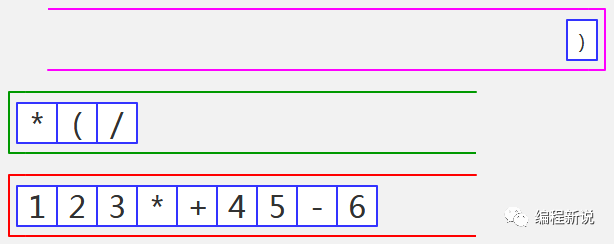
第十八步、读取到右括号，绿栈中运算符依次弹出并压入红栈，直至遇到左括号为止，如图32：

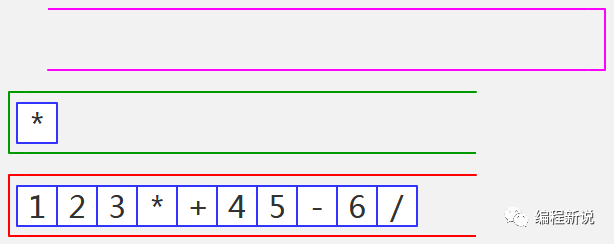
第十九步、TokenReader已空，绿栈中运算符依次弹出并压入红栈，直至全部弹出为止，如图33：

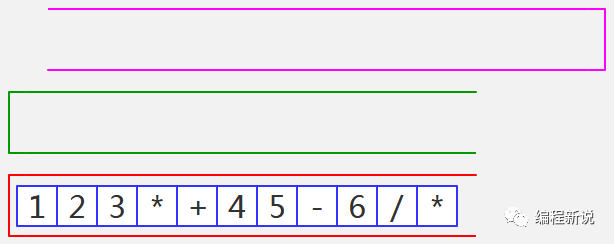
红栈中就是后缀表达式，栈底元素为表达式的头部，即从左到右便是。

中缀表达式转换为前缀表达式

中缀转前缀，先看视频，再看分步解析：

第一步、把中缀表达式装入TokenReader，并准备好从尾部开始读取，如图34：

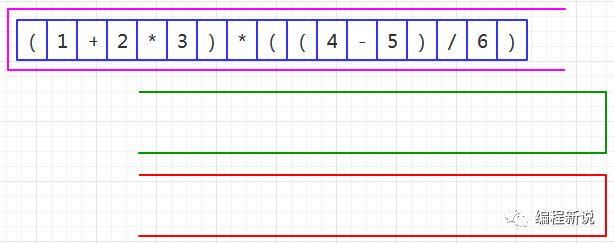
第二步、读取到右括号，压入绿栈，如图35：

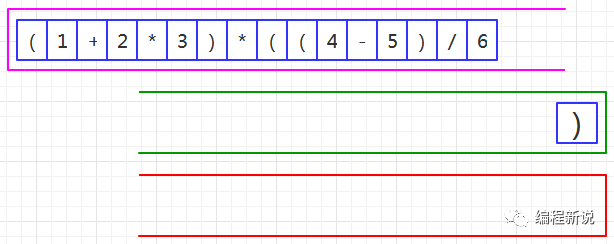
第三步、读取到操作数，压入红栈，如图36：

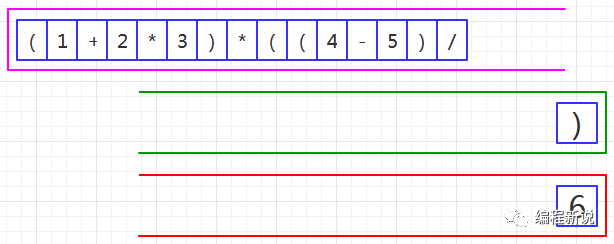
第四步、读取到除号，由于绿栈栈顶是右括号，所以压入绿栈，如图37：

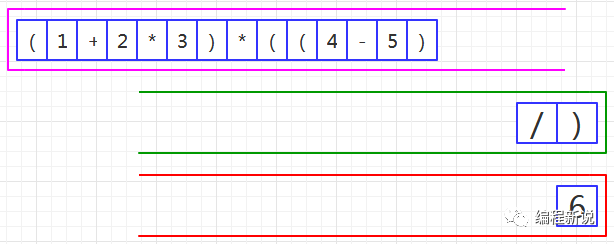
第五步、读取到右括号，压入绿栈，如图38：

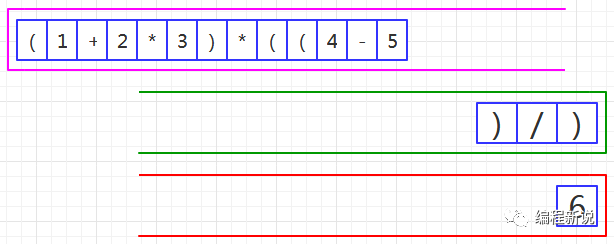
第六步、读取到操作数，压入红栈，如图39：

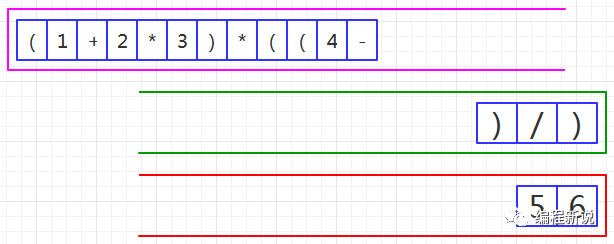
第七步、读取到减号，由于绿栈栈顶是右括号，所以压入绿栈，如图40：

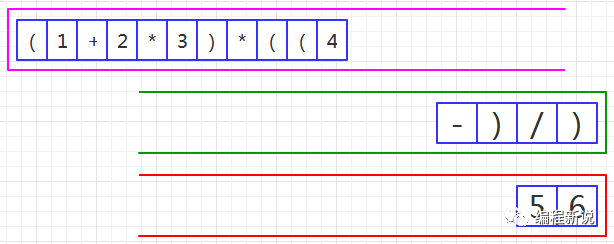
第八步、读取到操作数，压入红栈，如图41：

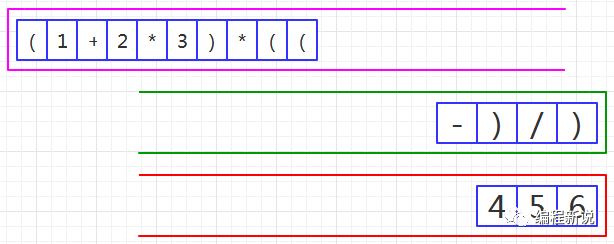
第九步、读取到左括号，绿栈中运算符依次弹出并压入红栈，直至遇到右括号为止，如图42：

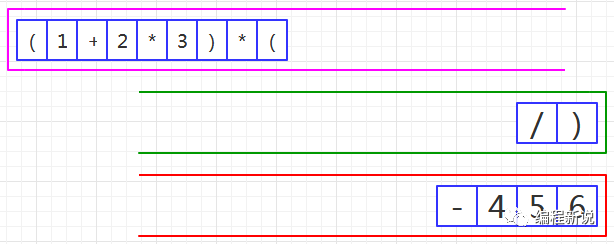
第十步、读取到左括号，绿栈中运算符依次弹出并压入红栈，直至遇到右括号为止，如图43：

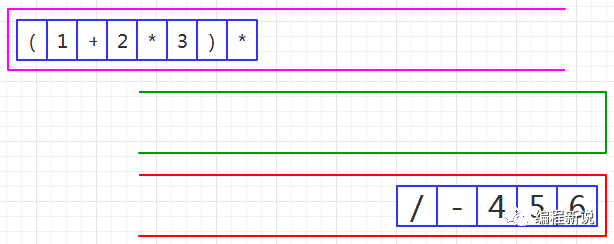
第十一步、读取到乘号，压入绿栈，如图44：

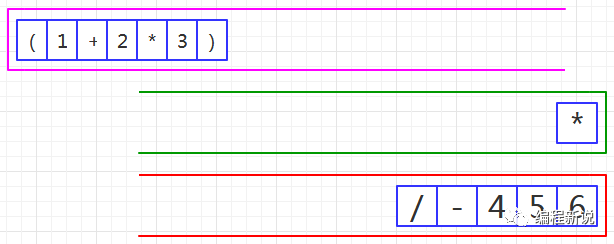
第十二步、读取到右括号，压入绿栈，如图45：

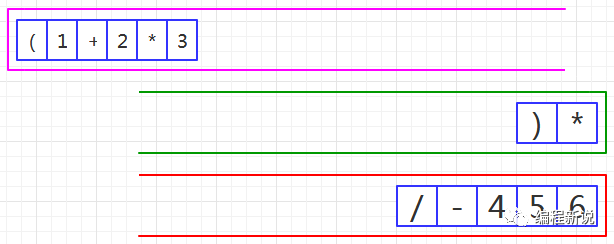
第十三步、读取到操作数，压入红栈，如图46：

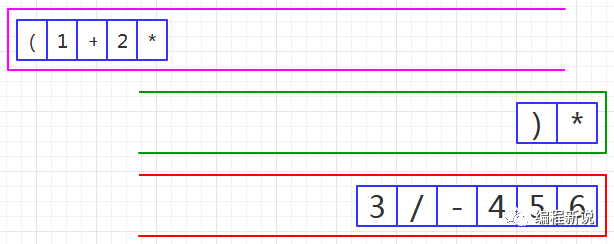
第十四步、读取到乘号，由于绿栈栈顶是右括号，所以压入绿栈，如图47：

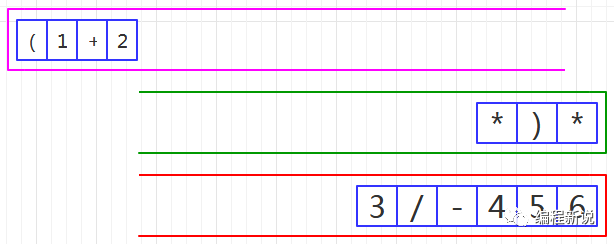
第十五步、读取到操作数，压入红栈，如图48：

第十六步、读取到加号，由于绿栈栈顶是乘号，优先级高，所以乘号弹出并压入红栈，再把加号压入绿栈，如图49：

第十七步、读取到操作数，压入红栈，如图50：

第十八步、读取到左括号，绿栈中运算符依次弹出并压入红栈，直至遇到右括号为止，如图51：

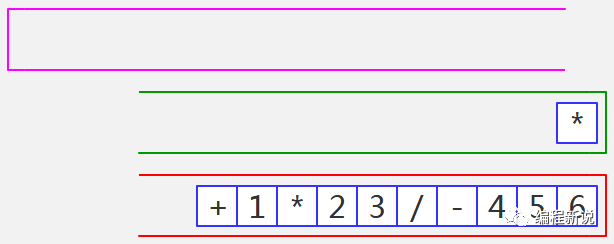
第十九步、TokenReader已空，绿栈中运算符依次弹出并压入红栈，直至全部弹出为止，如图52：

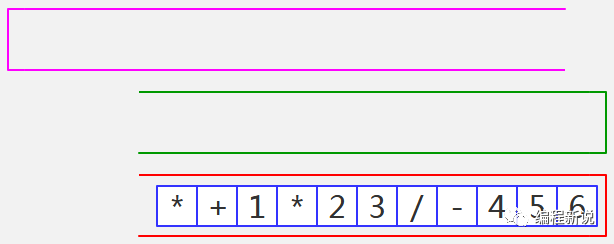
红栈中就是前缀表达式，栈顶元素为表达式的头部，即从左到右便是。

和作者一起来总结规律

中缀转后缀：

操作数总是入红栈
绿栈为空时，运算符总是入绿栈
左括号总是入绿栈
右括号总是导致运算符出绿栈，直至出到遇到左括号为止
同级别运算符总是入绿栈
高级别运算符总是入绿栈
低级别运算符总是导致运算符出绿栈，直至出到与低级别运算符的级别相同为止
最后，绿栈中的运算符必须全部出完

中缀转前缀：

操作数总是入红栈
绿栈为空时，运算符总是入绿栈
右括号总是入绿栈
左括号总是导致运算符出绿栈，直至出到遇到右括号为止
同级别运算符总是入绿栈
高级别运算符总是入绿栈
低级别运算符总是导致运算符出绿栈，直至出到与低级别运算符的级别相同为止
最后，绿栈中的运算符必须全部出完

可以看到仅仅是左右括号互换了一下，主要是因为一个是从左边开始扫描、一个是从右边开始扫描的缘故，除此之外，完全一致。

（END）

作者现任架构师，工作11年，Java技术栈，计算机基础，用心写文章，喜欢研究技术，崇尚简单快乐。追求以通俗易懂的语言解说技术，希望所有的读者都能看懂并记住。