在Cesium和其他三维开发中中经常用到矩阵变换。比如将一个物体移动、缩放、平移都可以用变换矩阵来计算。
再比如将三维场景中的物体转换为屏幕上显示的二维图形,需要用到透视投影(perspective projection)矩阵。
变换(tansformation)可是理解为一个函数,实现将一个空间坐标映射为另一个空间坐标,矩阵(matrix)是这种计算的一种方式,在三维开发中用途广泛。
最近在尝试其他三维平台,不能局限于Cesium。二维也有很多应用场景。
一、向量
1.1、向量的基本概念
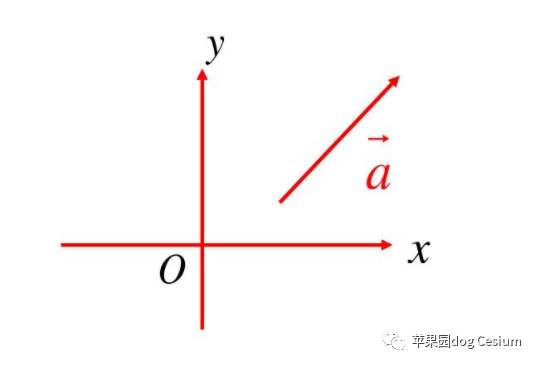
向量又称为矢量(vector),表示既有大小又有方向的量。在物理学中,力,速度,位移等都可以用向量来表示。
向量通常用一个有向线段表示。
1.2、向量的加法
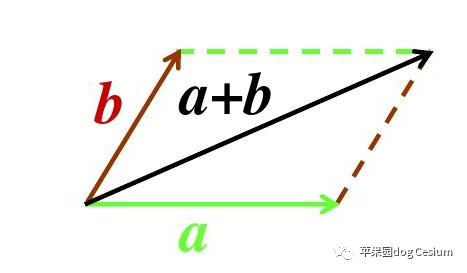
向量的加法运算符合平行四边形法则。
设向量a(x1,y1,z1)b(x2,y2,z2),则
a+b =(x1+x2,y1+y2,z1+z2)
1.3、向量的长度
向量的大小,也就是向量的长度(magnitude),也称为模,是一个标量。
设向量a(x,y),则向量a的长度记为|a|,公式如下,三维向量的公式同理。


1.4、归一化向量
向量的归一化就是把向量的长度变为1,方向保持不变。公式为:

向量v称为u的归一化(normalization)向量。
1.5、向量的点积和投影
向量的点积(dot product)又称为数量积(scalar product)或内积(inner product)。
向量的点积是一个标量,也就是一个数值。
设向量a,b,向量a和向量b的夹角,0≤θ≤π,则向量的点积公式如下:

设向量a(x1,y1,z1)b(x2,y2,z2),则
a·b=x1*x2+y1*y2+z1*z2
如果a·b=0,则成a和b是正交的。
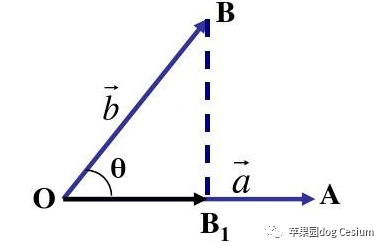
|OB1| =|b|cosθ ,|OB1| 称为b在向量a 方向上的投影。
投影向量如下,很容易推导。
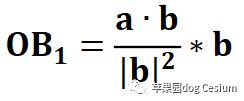
1.6、向量叉积
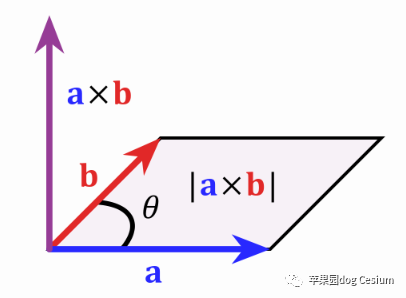
向量的叉积(cross product),又称外积(outer product)
设向量a和b的叉积为n,则n与a和b都正交,向量a,b和n构成一个右手坐标系(right-handed coordinate system)
叉积n的长度为:
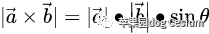
设向量a(xa,ya,za)b(xb,yb,zb),则
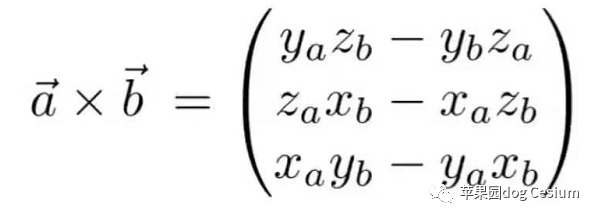
二、矩阵
2.1、矩阵的基本概念
由 m × n 个数aij排成的m行n列的数表称为m行n列的矩阵,简称m × n矩阵(引用百度百科)。记作:

这m×n 个数称为矩阵A的元素,简称为元,数aij位于矩阵A的第i行第j列。
(1)矩阵的加法
同型矩阵之间才可以进行相加。减法同理,就是对应元素相减。
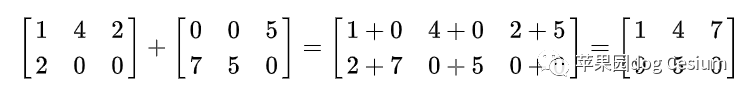
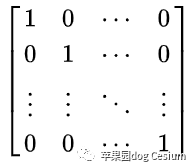
(2)单位矩阵
一个矩阵,从左上角到右下角的对角线(称为主对角线)上的元素均为1。除此以外全都为0,称为单位矩阵,通常记为E。
任何矩阵与单位矩阵相乘都等于本身。
(3)矩阵的转置
把矩阵A的行和列互相交换所产生的矩阵称为A的转置矩阵这一过程称为矩阵的转置。
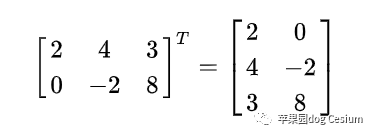
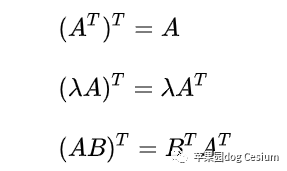
(4)逆矩阵
设A是一个n阶矩阵,若存在另一个n阶矩阵B,使得: AB=BA=E ,则称方阵A可逆,并称方阵B是A的逆矩阵,B=A-1
(5)矩阵乘法
两个矩阵相乘在三维变换中极为重要。
两个矩阵的乘法仅当第一个矩阵A的列数和另一个矩阵B的行数相等时才能定义。
比如一个4×4矩阵和4×1矩阵相乘得到的是一个4×1矩阵。
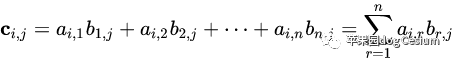
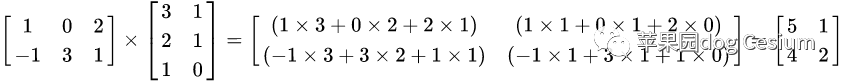
矩阵的乘法满足以下运算律:
结合律: (AB)C=A(BC)
左分配律:(A+B)C=AC+BC
右分配律:C(A+B)=CA+CB
矩阵不满足交换律 ,也就是AB != BA,这个在后面介绍的矩阵变换后会有直观的感受。
在三维开发中经常用到矩阵和矢量相乘,点和向量都可以用一个列矩阵来表示。
比如将一个空间中的点P(x,y,z)左乘一个3✖3的矩阵得到新的坐标P1(x',y',z')。
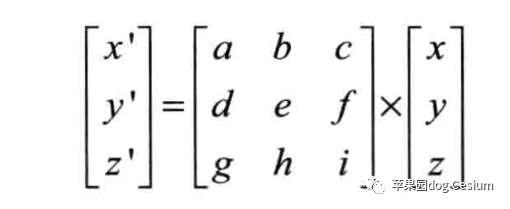
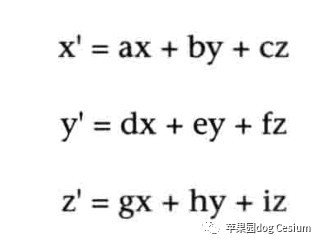
2.2、平移变换
平移(translation)变换是把空间中一个点沿着给定的方向移动固定的距离,设位移向量d,点P移动后P1,则 P1=P+d;
如果用齐次坐标(homogeneous coordinate)表示点和向量(齐次坐标的概念请自行查阅资料学习),
设点P(x,y,z,1),点P1(x',y',z',1),向量d=(tx,ty,tz,0),则
x'=x+tx
y'=y+ty
z'=z+tz
表示成矩阵形式如下:
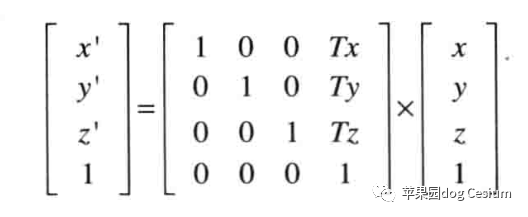
平移变换矩阵即为:

2.3、旋转
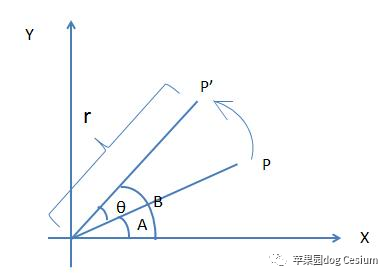
计算点p绕着z轴旋转θ角后的p‘的坐标,r为OP的长度。
x=rcosA
y=rsinA
x'=rcos(A+θ)
y'=rsin(A+θ)
利用两角和的三角函数公式可得到
x'=xcosθ - ysinθ
y'=xsinθ + ycosθ
z'=z
用矩阵表示,绕Z轴旋转的变换矩阵为:
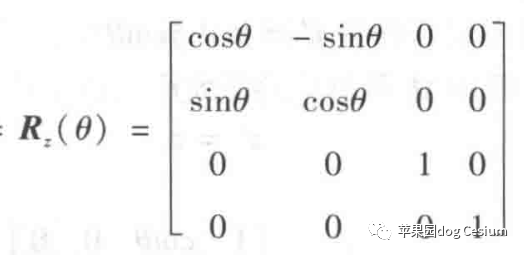
绕X轴旋转的变换矩阵为:
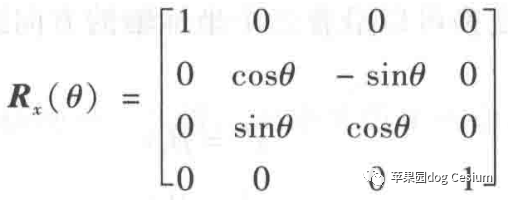
绕Y轴变换的矩阵
2.4、缩放
假设在X轴,Y轴,Z轴上的缩放因子分别为Sx,Sy,S
2.6、模型视图投影矩阵
这个以后再说
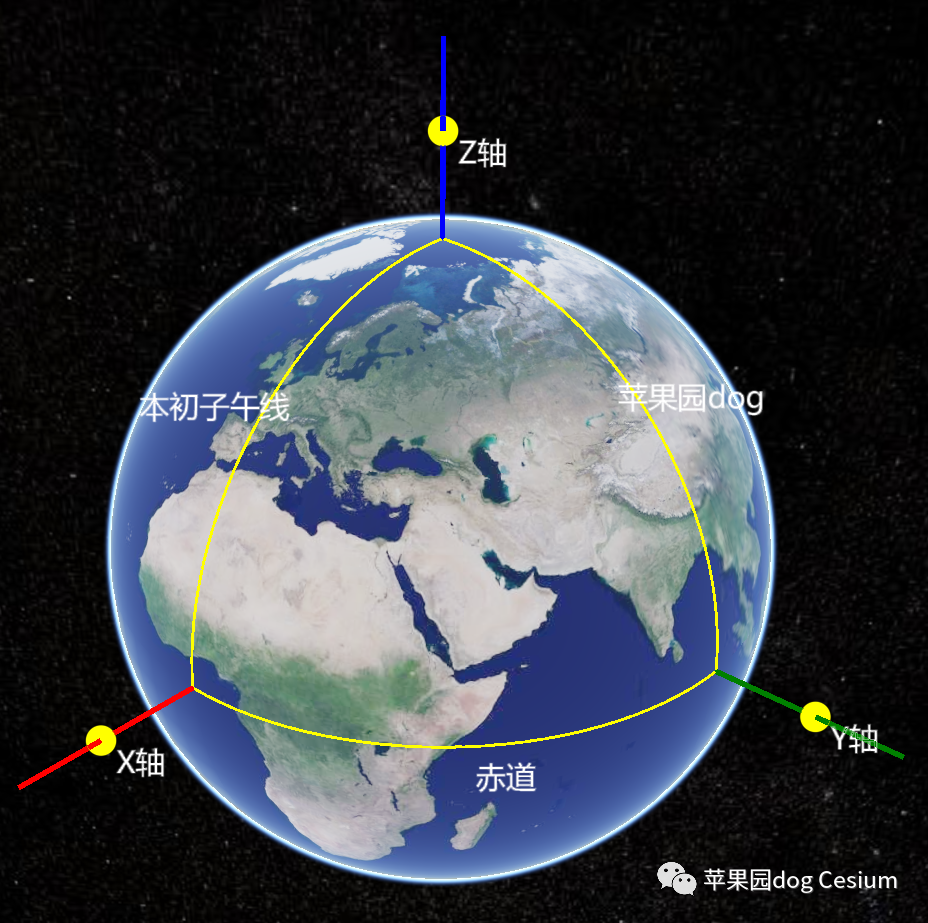
三、Cesium中的坐标系
Cesium中的地球默认采用的是WGS84坐标系。
改天再写
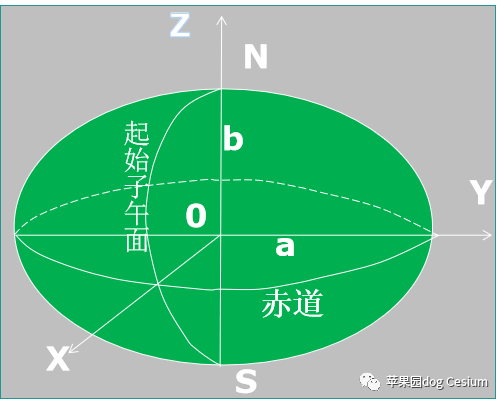
四、Cesium中的矩阵变换
改天再写
五、相关示例
改天再写
methods: {
update3DtilesHeight(tileset, heightChange) {
if (!tileset) {
return
}
try {
let translation = Cesium.Matrix4.getTranslation(tileset.root.transform, new Cesium.Cartesian3()) //从世界坐标中心点到局部坐标系(一般移到球表面之上)的平移向量
var m = Cesium.Transforms.eastNorthUpToFixedFrame(translation) //将平移向量转变为4x4变换矩阵
//let positionDegree = cesiumCoordUtil.cartesian3ToDegree2(translation);//平移向量转为WGS84坐标
let newTran = new Cesium.Cartesian3(0, 0, heightChange) //平移向量
Cesium.Matrix4.multiplyByTranslation(m, newTran, m) //平移变换
let newPos = Cesium.Matrix4.getTranslation(m, new Cesium.Cartesian3())
Cesium.Matrix4.setTranslation(tileset.root.transform, newPos, tileset.root.transform)
//cesium3dTilesUtil.flyTo3dtiles(tileset);
} catch (error) {
console.log(error)
}
}
},
//生命周期 - 创建完成(可以访问当前this实例)
created() {},
//生命周期 - 挂载完成(可以访问DOM元素)
mounted() {
cesiumCommon.init3D()
let that = this
var center = Cesium.Cartesian3.fromDegrees(116, 39, 0)
//var center2 = Cesium.Cartesian3.fromDegrees(116.5, 39.3, 0)
// var transform = Cesium.Transforms.eastNorthUpToFixedFrame(center)
// var referenceFramePrimitive = viewer.scene.primitives.add(
// new Cesium.DebugModelMatrixPrimitive({
// modelMatrix: transform,
// length: 100000.0
// })
// )
// var redRectangle = viewer.entities.add({
// name: 'Red translucent rectangle',
// rectangle: {
// coordinates: Cesium.Rectangle.fromCartesianArray([center, center2]),
// material: Cesium.Color.RED.withAlpha(0.5)
// }
// })
//cesiumLocateUtil.flyToRectangle([center, center2], 0, -45, 3, 2, function () {})
// var tileset = viewer.scene.primitives.add(
// new Cesium.Cesium3DTileset({
// url: Cesium.IonResource.fromAssetId(486976)
// })
// )
//viewer.flyTo(tileset)
var tileset = viewer.scene.primitives.add(
new Cesium.Cesium3DTileset({
url: 'http://localhost:8083/tileset.json',
modelMatrix: Cesium.Matrix4.fromArray([1, 0, 0, 0, 0, 1, 0, 0, 0, 0, 1, 0, 0, 0, 0, 1])
})
)
tileset.readyPromise
.then(function (tileset) {
var v = [10, 0, 0, 0, 0, 10, 0, 0, 0, 0, 10, 0, 0, 0, 0, 1]
/**
*
* 100 0 0 0
* 0 100 0 0
* 0 0 100 0
* 0 0 0 1
*
*/
let newTranslation = new Cesium.Cartesian3()
Cesium.Matrix4.getTranslation(tileset.root.transform, newTranslation)
let tilesetHight = Cesium.Cartographic.fromCartesian(newTranslation).height
console.log(tilesetHight)
that.update3DtilesHeight(tileset, 0)
viewer.entities.add({
//position:Cesium.Matrix4.multiplyByPoint(tileset.root.transform, new Cesium.Cartesian3(0,0,1), new Cesium.Cartesian3()),
position:newTranslation,
point: {
pixelSize: 10,
color: Cesium.Color.YELLOW
}
})
// let a = tileset.root.computedTransform
// let b = tileset.root.transform
// console.log(b)
// console.log(a)
// let scaleMatrix = Cesium.Matrix4.fromArray(v) //缩放变换矩阵
// let translationCartesian3 = new Cesium.Cartesian3()
// Cesium.Matrix4.getTranslation(b, translationCartesian3) //得到笛卡尔地心坐标中心到模型中心的平移向量
// var center2 = Cesium.Cartesian3.fromDegrees(116.5, 39.3, 0)
// var transform = Cesium.Transforms.eastNorthUpToFixedFrame(center)
// var redRectangle = viewer.entities.add({
// name: 'Red translucent rectangle',
// rectangle: {
// coordinates: Cesium.Rectangle.fromCartesianArray([center, center2]),
// material: Cesium.Color.RED.withAlpha(0.5),
// height:0
// }
// })
var referenceFramePrimitive = viewer.scene.primitives.add(
new Cesium.DebugModelMatrixPrimitive({
modelMatrix: tileset.root.transform,
length: 100000.0
})
)
tileset.show=true
// let tanslationMatrix4 = new Cesium.Matrix4()
// Cesium.Matrix4.fromTranslation(translationCartesian3, tanslationMatrix4) //得到平移矩阵
// let negativeTanslation = new Cesium.Cartesian3()
// Cesium.Cartesian3.negate(translationCartesian3, negativeTanslation) //得到平移向量的逆向量
// let negativeTanslationMatrix4 = new Cesium.Matrix4()
// Cesium.Matrix4.fromTranslation(negativeTanslation, negativeTanslationMatrix4) //得到逆向量的平移矩阵
// Cesium.Matrix4.multiply(negativeTanslationMatrix4, tileset.root.transform, tileset.root.transform) //平移矩阵乘以原始矩阵,将模型平移到原点
// Cesium.Matrix4.multiply(scaleMatrix, tileset.root.transform, tileset.root.transform) //缩放变换
// Cesium.Matrix4.multiply(tanslationMatrix4, tileset.root.transform, tileset.root.transform) //再平移回原来的位置
// let newTranslation2 = new Cesium.Cartesian3()
// Cesium.Matrix4.getTranslation(tileset.root.transform, newTranslation2)
// let tilesetHight2 = Cesium.Cartographic.fromCartesian(newTranslation2).height
// console.log(tilesetHight2);
//var scaleMatrix = Cesium.Matrix4.fromScale(new Cesium.Cartesian3(7.0, 8.0, 9.0));
//tileset.root.transform=Cesium.Matrix4.multiply(scaleMatrix, tileset.root.transform, new Cesium.Matrix4());
})
.otherwise(function (error) {
callback(null, error)
})
viewer.flyTo(tileset)






