“ 前面咱们学习了统计知识,但一直没有结合到Python来进行实操,所以咱们这次来补充scipy库关于统计类的操作。”
01
—
scipy库
SciPy 是建立在 Python 的 NumPy 扩展之上的数学算法和便利函数的集合。大家可以直接在官网上进行学习,同理各个库官网学习结合博主文释是很好的途径:https://docs.scipy.org/doc/scipy/reference/tutorial/general.html
包含了以下子库:
分包 | 描述 |
|---|---|
| 聚类算法 |
| 物理和数学常数 |
| 快速傅立叶变换例程 |
| 积分和常微分方程求解器 |
| 插值和平滑样条 |
| 输入和输出 |
| 线性代数 |
| N维图像处理 |
| 正交距离回归 |
| 优化和寻根程序 |
| 信号处理 |
| 稀疏矩阵和相关例程 |
| 空间数据结构和算法 |
| 特殊功能 |
| 统计分布和函数 |
SciPy 子包需要单独导入,例如:
from scipy import stats
我们着重放在stats统计这个子库标黄部分上,它包含大量概率分布、汇总和频率统计、相关函数和统计检验、屏蔽统计、核密度估计、准蒙特卡罗功能等。
统计是一个非常大的领域,有些主题超出了 SciPy 的范围,并被其他软件包覆盖。其中一些最重要的是:
statsmodels:回归、线性模型、时间序列分析、对主题的扩展也由
scipy.stats
.Pandas:表格数据、时间序列功能、与其他统计语言的接口。
PyMC3:贝叶斯统计建模,概率机器学习。
scikit-learn:分类、回归、模型选择。
Seaborn:统计数据可视化。
rpy2:Python 到 R 的桥接。
02
—
如何画各种分布图
之前咱们可以通过公式去画一个正态分布图,
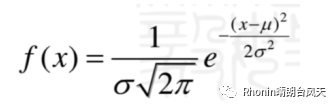
import mathimport numpy as npimport matplotlib.pyplot as pltu = 0 # 均值μsig = math.sqrt(1) # 标准差δx = np.linspace(u - 3*sig, u + 3*sig, 50) # 定义域y = np.exp(-(x - u) ** 2 (2 * sig ** 2)) (math.sqrt(2*math.pi)*sig) # 定义曲线函数plt.plot(x, y, "g", linewidth=2) # 加载曲线plt.grid(True) # 网格线plt.show() # 显示
嗯,有点长,那么scipy又是怎么操作的呢?没有公式,只需要定义好x,均值,标准差即可。
一个正常的连续随机变量:scipy.stats.norm.rvs(loc=0, scale=1, size=1, random_state=None)随机变量/.pdf(x, loc=0, scale=1),概率密度函数,画正态分布
from scipy import statsimport numpy as npimport matplotlib.pyplot as pltmu=0sigma=1x=np.arange(-5,5,0.1)y=stats.norm.pdf(x,mu,sigma)plt.plot(x,y)
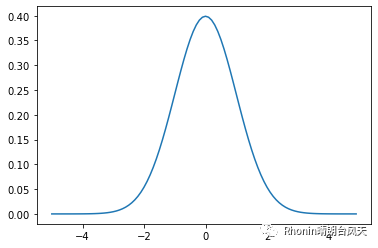
有没让图看起来吊炸天那种,我想说有是有的,只是你们自己去加吧,哈哈
再来画个泊松分布,如果不记得,可回顾统计-5 正态分布是概率分布的神
泊松离散随机变量:scipy.stats.poisson.pmf(k, mu, loc=0)
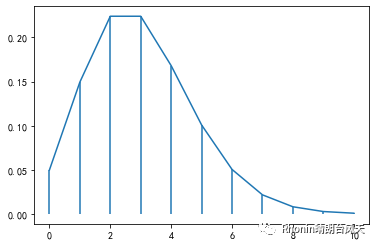
import numpy as npfrom scipy import statsimport matplotlib.pyplot as pltlam=3 #λ为单位时间内事件的平均发生次数k=10 #k为事件发生次数x=np.arange(0,k+1,1)plist=stats.poisson.pmf(x,lam) #返回列表,1、2、3……次的概率print(plist)plt.plot(x,plist)plt.vlines(x,0,plist)plt.show()
再来个二项分布,一般情况下,出现A的概率是p,B的概率是1-P,这类实验被称为伯努利试验,比如典型的抛硬币,而A会发生x次,则失败次数为n-x,二项分布求的是成功x次的概率,叫二项是因为只有2种结果。
二项式离散随机变量:scipy.stats.binom.pmf(k, n, p, loc=0)
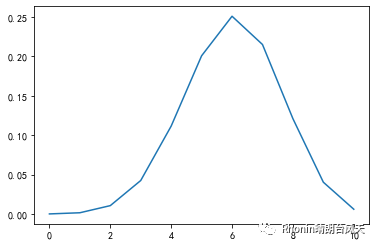
import numpy as npfrom scipy import statsimport matplotlib.pyplot as pltp=0.6 #假设事件A概率0.6n=10 #次数x=np.arange(0,n+1,1)plist=stats.binom.pmf(x,n,p) #返回列表,对应概率plt.plot(x,plist)plt.show()
二项分布求解的问题是成功x次的概率,而几何分布,试验x次,才取得第一次成功的概率。
scipy.stats.geom.pmf(k, p, loc=0)
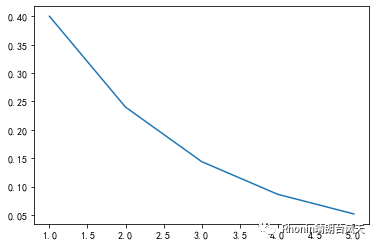
import numpy as npfrom scipy import statsimport matplotlib.pyplot as pltk=5 #5次就成功的概率p=0.4 #成功概率x=np.arange(1,k+1,1)plist=stats.geom.pmf(x,p)print(plist)plt.plot(x,plist)plt.show()
03
—
再认识更多分布
我们已经学了正态分布、t分布、F分布、卡方分布、幂律分布、泊松分布,再补充一些其它分布。
1、指数分布,不同的独立事件发生之间时间间隔值的分布,时间越长发生的概率指数型增大(减小),在我们日常的消费领域,通常的目的是求出在某个时间区间内,会发生随机事件的概率有多大。

2、均匀分布也叫矩形分布,它是对称概率分布,在相同长度间隔的分布概率是等可能的。
3、0-1分布(伯努利分布)

4、超几何分布,描述了从有限N个物件(其中包含M个指定种类的物件)中抽出n个物件,成功抽出该指定种类的物件的次数(不放回)。

我个人感觉比较容易混淆的是,泊松分布、超几何分布、几何分布。建议都看看概念。
04
—
scipy概率分布总结
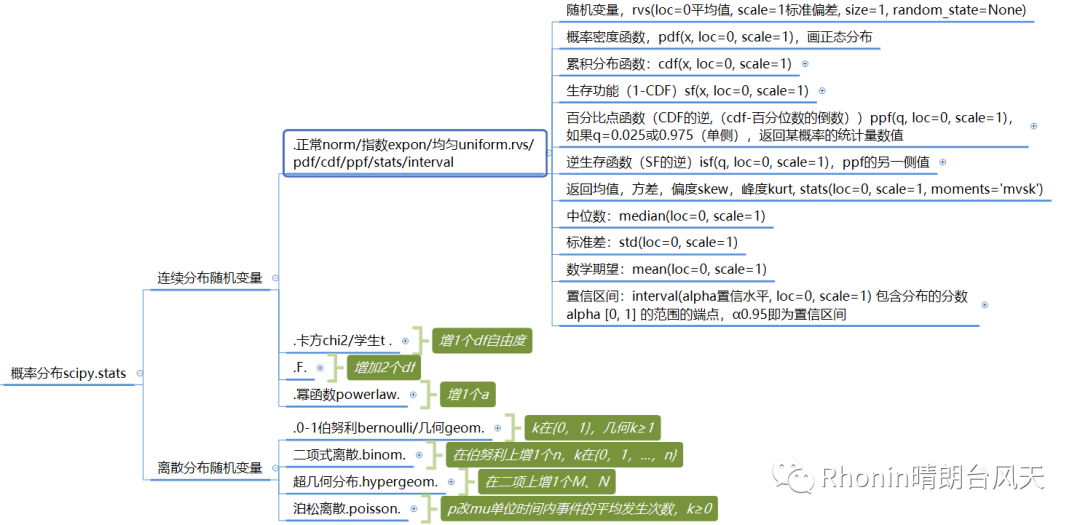
一、概率分布scipy.stats,不管你是哪种类型的分布,方法都是通用的,主要都是以下几类,但内部填充的数据会有所不同。
1、产生随机变量
rvs(loc=0平均值, scale=1标准偏差, size=1数量或形状都可以, random_state=None)
2、概率密度函数,画图一般用来做Y轴,前面第一部分已有示例。
连续:pdf(x, loc=0, scale=1)
离散:pmf(k, p, loc=0)
3、累积分布函数:
cdf(x, loc=0, scale=1)
4、生存功能
(1-CDF)sf(x, loc=0, scale=1)
栗子用标准正态分布,留意结果输出对比差异。
from scipy import statsimport numpy as npimport matplotlib.pyplot as pltx=np.arange(0,3)stats.norm.cdf(x)#结果输出array([0.5 , 0.84134475, 0.97724987])stats.norm.sf(x)#结果输出array([0.5 , 0.15865525, 0.02275013])
5、百分比点函数(CDF的逆,(cdf-百分位数的倒数))
ppf(q, loc=0, scale=1),如果q=0.025或0.975(单侧),返回某概率的统计量数值
6、逆生存函数(SF的逆)
isf(q, loc=0, scale=1),ppf的另一侧值
栗子用标准正态分布,留意结果输出对比差异。
stats.norm.ppf(0.975)Out[25]: 1.959963984540054stats.norm.isf(0.975)Out[27]: -1.959963984540054
7、返回均值,方差,偏度skew,峰度kurt,
stats(loc=0, scale=1, moments='mvsk')
8、中位数:median(loc=0, scale=1)
9、标准差:std(loc=0, scale=1)
10、数学期望:mean(loc=0, scale=1)
11、置信区间:interval(alpha置信水平, loc=0, scale=1) 包含分布的分数 alpha [0, 1] 的范围的端点,α0.95即为置信区间
栗子用标准正态分布,95%
stats.norm.interval(0.95)Out[21]: (-1.959963984540054, 1.959963984540054)
二、各分布方法的区别
1、由下图可知,正态分布、指数分布、均匀分布方法是通用的,其它分布也是在这个的基础上小范围区别。

2、.卡方chi2/学生t .,是在正态分布方法的基础上增加了1个df自由度

3、.F.分布是在正态分布方法基础上增加2个df

4、.幂函数powerlaw.,在正态分布方法上增加1个a

5、分散分布会有些不同,主要是在k\p上
.0-1伯努利bernoulli/几何geom.,其中伯努利k在{0,1},几何k≥1

6、二项式离散.binom.,在伯努利上增1个n,k在{0,1,…,n}

7、超几何分布.hypergeom.,在二项上增1个M、N

8、泊松离散.poisson.,伯努利上p改mu单位时间内事件的平均发生次数,k≥0

感慨一句,自学不易,特别是接触新知识,人的理解力会变差。但你琢磨几天豁然开朗后又会觉得不过如此。 这是一定要经历的过程嘛?
这是一定要经历的过程嘛?







