“ 不得不感慨一句,为了减少误差,检验过程中的‘小心‘真的达到了令我叹为观止的地步,因为我花了整整10天绞尽脑汁各个课程中穿梭反复研究假设检验。”
备注:详细版在文末
01
—
变量类型与参数估计
一、变量类型
这算是比较小白的问题,不过还是要单独拿出来再说,当然不同课程不同老师对此类定义有不同,我个人感觉主要三大类,可以自己慢慢体会。像第二种其实表达的都是同一种。罗列出来主要是为了以后大家知道什么类型变量对应什么检验法。

二、参数估计
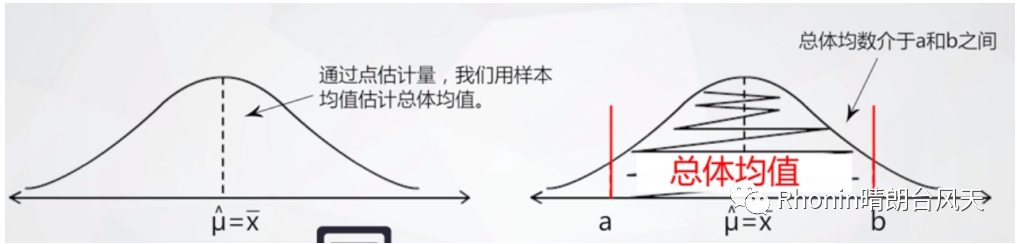
分为点估计和区间估计,别看那些老师讲得高深莫测的,只要记住区间估计更科学就可以了。
举个例子,猜我今天钱包里装了多少钱,猜对我请你吃饭,猜错你请我吃饭。你说200的话那可能你要请吃饭了,如果你说0-10000就我要请吃饭,就是这个差别,嘿嘿,反正肯定猜区间。
02
—
正态分布是概率分布的神
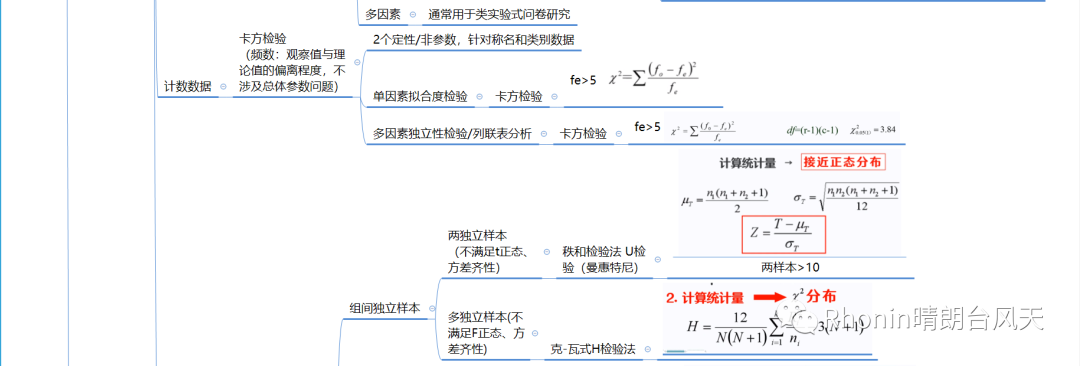
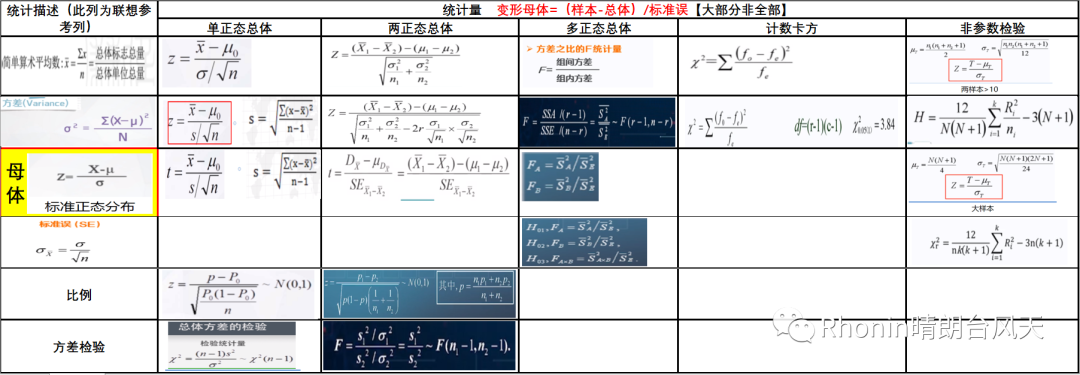
除了正态分布的Z检验外,常用的还有小样本t检验、卡方检验、F检验,以及非参数检验。
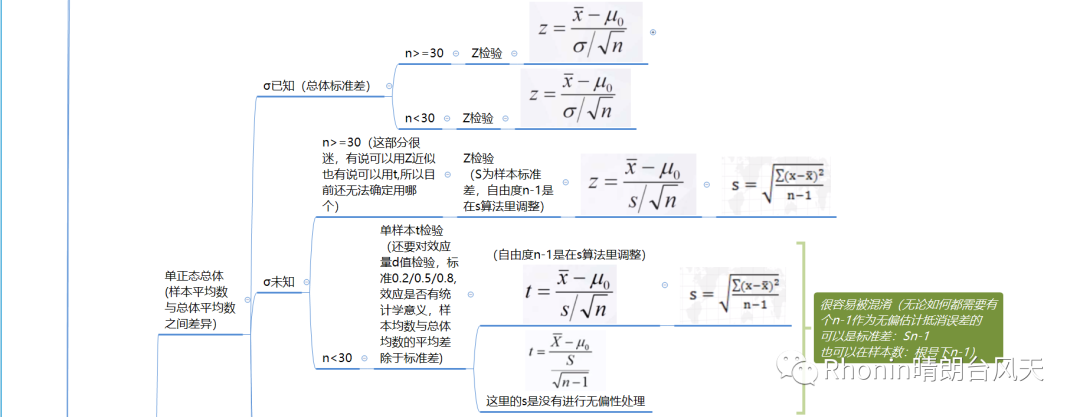
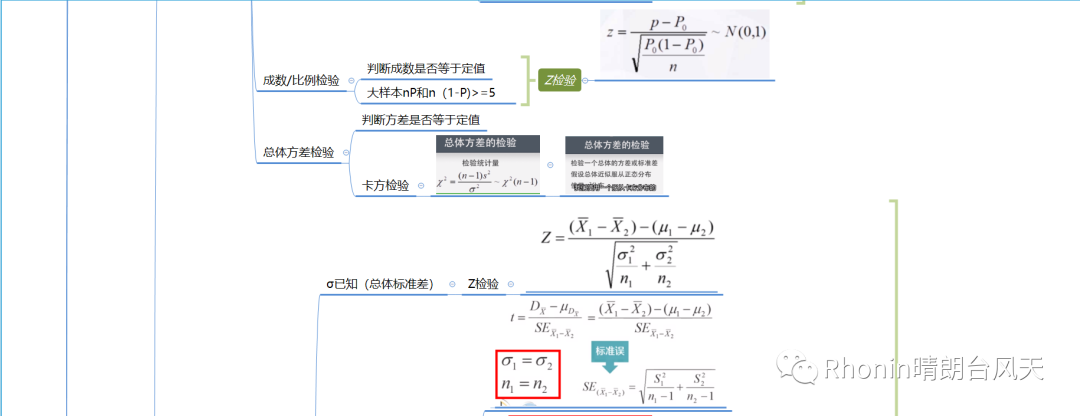
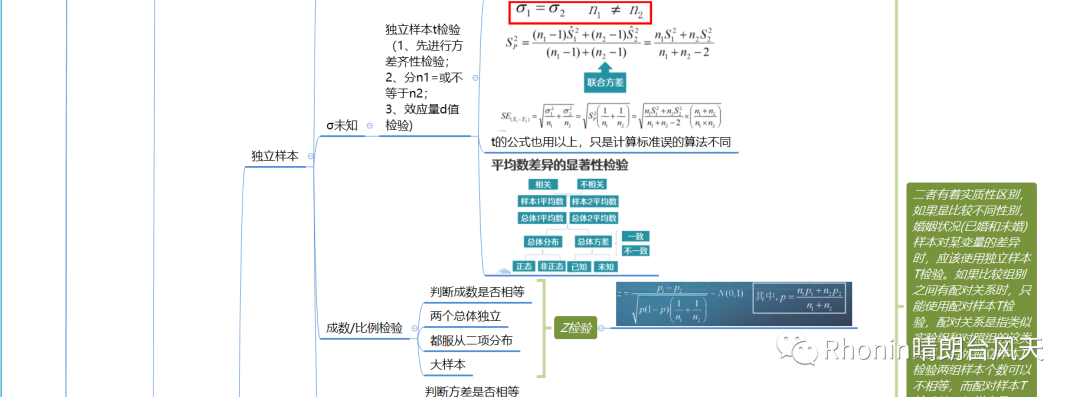
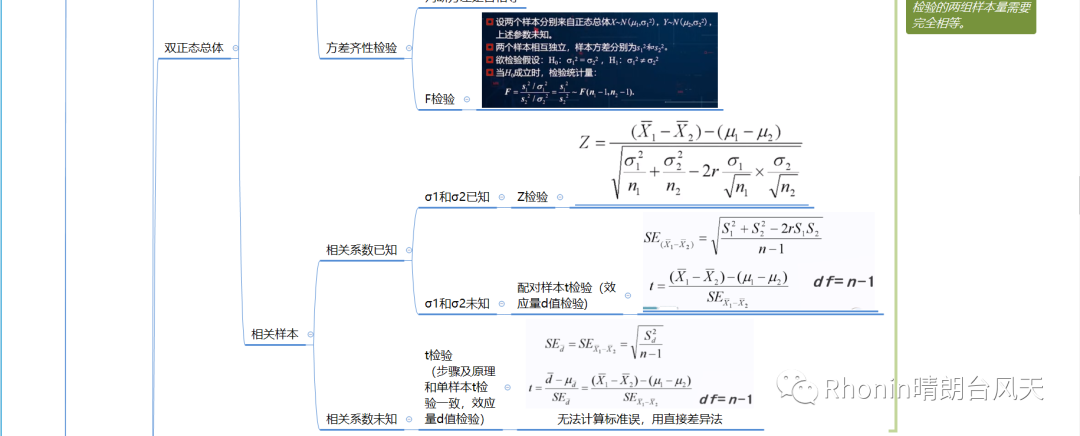
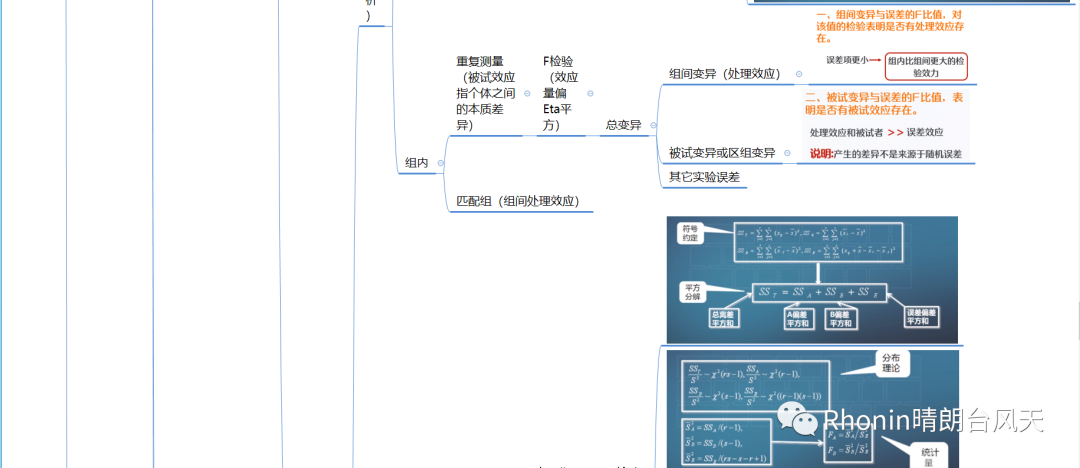
所有分布,不是正态分布就是在形成正态分布的路上。我把以上涉及的检验统计量数学公式罗列出来,我们从第一列去联想,再观察整个统计量,你会惊讶发现那些繁琐复杂的数学公式,都是通过母体=(样本-总体)/标准误【大部分非全部】变形出来,如果你再看得仔细一点都是基本上都是围绕标准误变形。
而更复杂的也不过是组间组内方差的计算。
如果能熟知数学公式固然好,但你写不出也没关系。所以别害怕,抓住母体,利用好各种软件就可以快速达到目的了。
03
—
被绑架的自由度
一般自由度df=n-k都是在总体方差未知情况下,t检验、F检验、卡方检验都要进行n-1。因为总体方差未知,所以我们会用样本方差来代替,总体方差是期望值可以直接除于n,但样本方差不等于总体方差,要进行无偏性处理。而样本方差我们可以通过计算获取,百度曰:所以大小为n的样本中只要n-1个数确定了,第n个数就只有一个能使样本符合样本平均数的数值。也就是说,样本中只有n-1个数可以自由变化,只要确定了这n-1个数,方差也就确定了。这里,样本平均数就相当于一个限制条件,由于加了这个限制条件,样本方差s的自由度为n-1。
04
—
假设检验
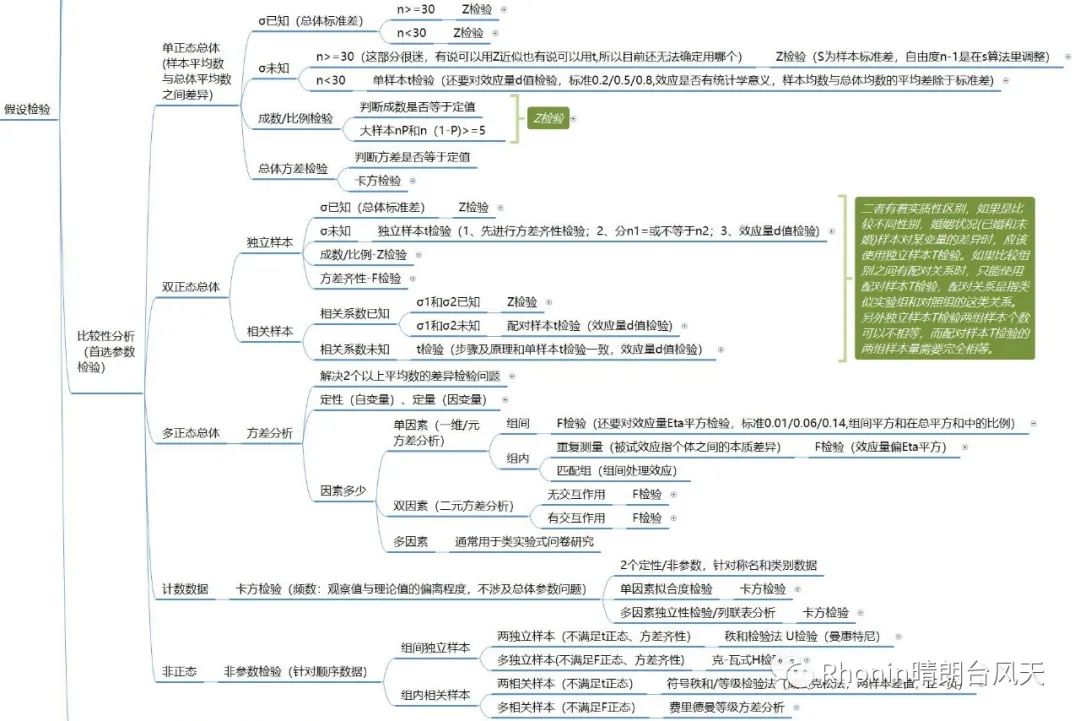
来一波非常详细的长图吧,很多情况特殊的我在里面都有说明。文章开头贴了简易版,也是可以用的!
之所以很多前提条件,其实都是为了小心、小心再小心验证!为了减少误差,提高置信度,让你的结论真正有说服力,这么多统计大师贡献才有下面长图。
突然发现我花了10天心血文章用字最少……额…… 如果你没底子要消化一下长图估计也要跟我一样花不少时间,我能弄懂,你也可以,加油!
如果你没底子要消化一下长图估计也要跟我一样花不少时间,我能弄懂,你也可以,加油!