“ 1、概率可以改变宿命
2、数学期望可以改变穷人思维
3、大数定律告诉别纠结过去坚持做正确的事
4、用贝叶斯的思路不断迭代你的决策系统
5、方差让你认识风险更好去投资”
我们所生活的世界,是一个随机有好有坏不完美的世界,千万不要被绝望感裹挟。因为我们可以通过行动将好的放大,坏的缩小。而时间权、空间权和概率权就是我们放大缩小的工具。
01
—
大数定律与中心极限定理
概率论的两大”黄金定理“分布是大数定律和中心极限定理,前面有介绍过大数定律,而中心极限定理就是今天要说的正态分布的数学证明。
中心极限定理,大量独立的随机变量相加,无论各个随机变量的分布是怎样的,它们相加的结果必定会趋向于正态分布。换句通俗话来说就是样本均值约等于总体均值。。

重点理解一下两大黄金定理的区别:直观上来讲,想到大数定律的时候,你脑海里浮现的应该是一个样本,而想到中心极限定理的时候脑海里应该浮现出很多个样本。
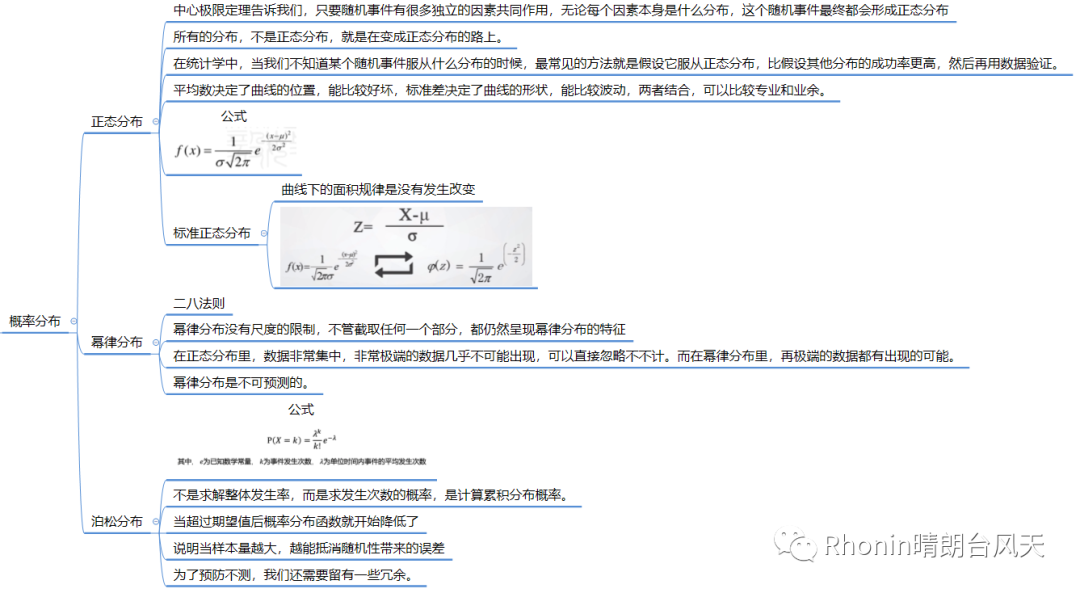
好,我们再回去看看标准差和标准误差(样本>=30)的区别:统计-4 统计描述:高风险高收益
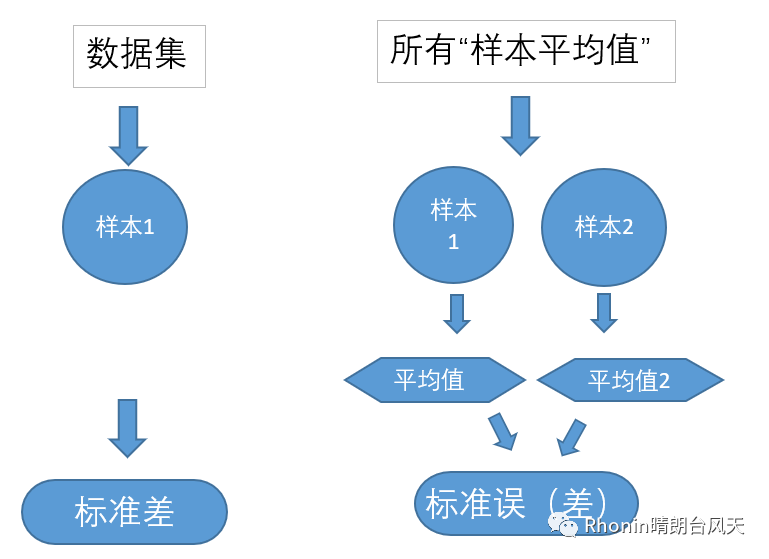 标准误公式:
标准误公式:
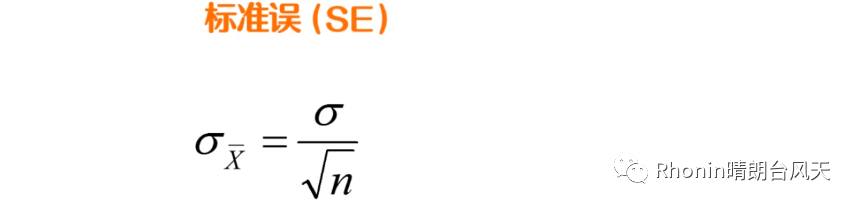
02
—
所有的分布,不是正态分布,就是在变成正态分布的路上
我们把随机事件不同结果和对应的概率全部统计出来后,我们把概率进行一个排列分布,在此前用一首古诗形容:“横看成岭侧成峰,远近高低各不同。不识庐山真面目,只缘身在此山中”。
通过分布我们突然看清了整个随机事件,发现概率的分布其实很多是暗含规律的。我们也用一句古诗形容这种上帝的视角:“会当凌绝顶,一览众山小”。这样也就和我们前文说的从局部的不确定性转变成整体的确定性了。
正态分布(也叫高斯分布)是我们从概率分布里发现的最重要也最简单的一种。normal distribution,直接翻译过来就是“正常的分布”“一般的分布”,关键:中心极限定理告诉我们,只要随机事件有很多独立的因素共同作用,无论每个因素本身是什么分布,这个随机事件最终都会形成正态分布。也就说明它普遍存在。更夸张的是任何分布叠加最终都会形成正态分布,所以无论是对数分布还是幂律分布,无论是指数分布还是其他任何分布,只要自身不断演化,不断自己叠加自己,最终也一样会变成正态分布。所以,所有的分布,不是正态分布,就是在变成正态分布的路上。按照正态分布的钟形曲线分布和演化,就是每个随机事件的必然宿命,好像冥冥中自有定数。正态分布是概率分布的神!(引用借鉴了刘嘉老师精彩精确描述,但最让我震撼的是这句话。推荐大家学习刘嘉老师的概率论)
在统计学中,当我们不知道某个随机事件服从什么分布的时候,最常见的方法就是假设它服从正态分布,比假设其他分布的成功率更高,然后再用数据验证。
1、平均数决定了曲线的位置,能比较好坏,标准差决定了曲线的形状,能比较波动,两者结合,可以比较专业和业余。

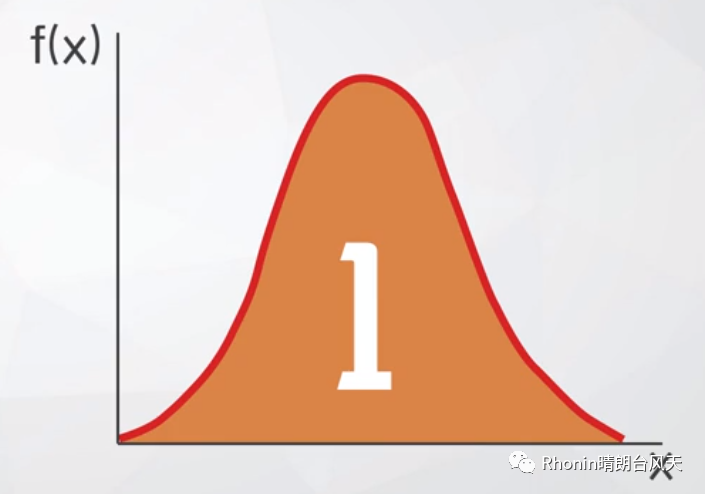
2、曲线下面积等于1
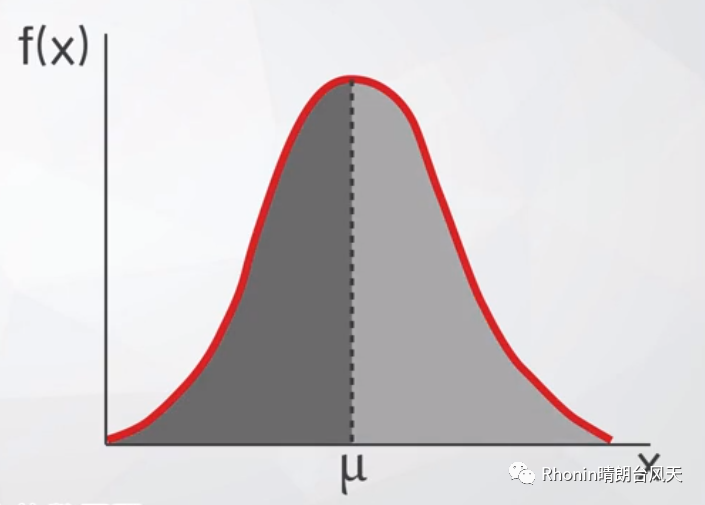
3、以均数为中心,左右对称
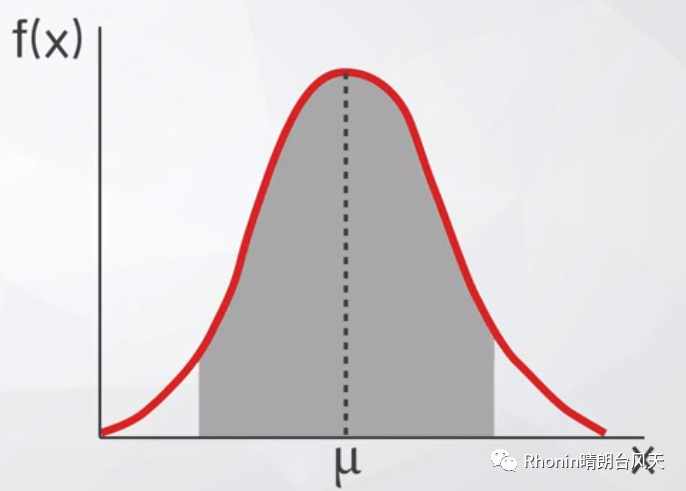
4、频数集中于均数周围
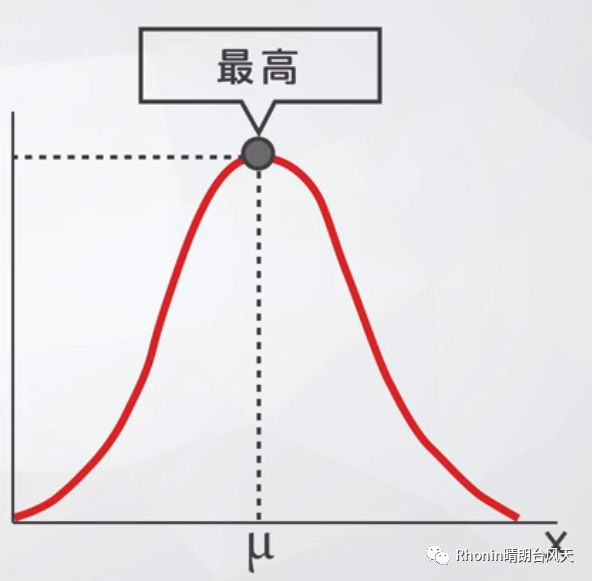
5、正态分布最高点所对应X轴的值为数据的平均数
6、正态分布的公式:

import mathimport numpy as npimport matplotlib.pyplot as pltu = 0 # 均值μsig = math.sqrt(1) # 标准差δx = np.linspace(u - 3*sig, u + 3*sig, 50) # 定义域y = np.exp(-(x - u) ** 2 (2 * sig ** 2)) (math.sqrt(2*math.pi)*sig) # 定义曲线函数plt.plot(x, y, "g", linewidth=2) # 加载曲线plt.grid(True) # 网格线plt.show() # 显示
7、标准正态分布
统计-4 统计描述:高风险高收益
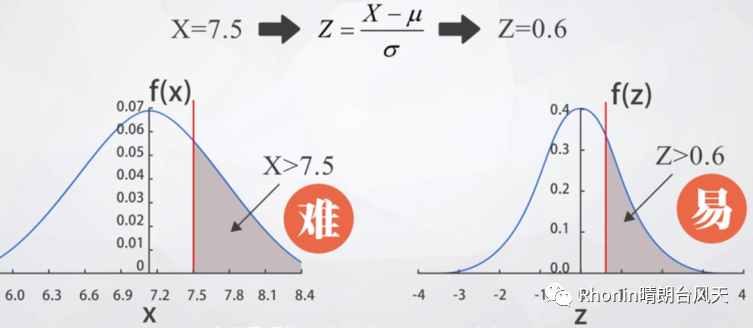
前面咱们聊过标准Z分数,聊过标准差的来源,把任何正态分布转变成标准正态分布是同理。
标准正态分布与任何正态分布曲线下的面积规律是没有发生改变的,所以我们可以通过转换可以轻易计算。
转变公式:
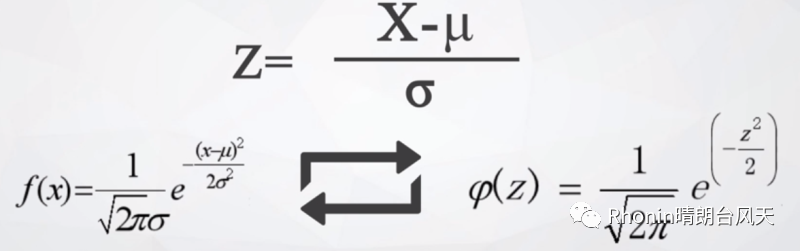
03
—
幂律分布
在咱们电商商品里经常出现销售前20%的商品往往占到销售额的80%,这是传说中的28法则,28法则也是幂律分布最直观的体现。

幂律分布没有尺度的限制,不管截取任何一个部分,都仍然呈现幂律分布的特征。
而且电商行业选取关键词往往会选取长尾词来做商品标题,长尾也叫肥尾,很多金融现象也会经常发生。在正态分布里,数据非常集中,非常极端的数据几乎不可能出现,可以直接忽略不不计。而在幂律分布里,再极端的数据都有出现的可能。
幂律分布是不可预测的。
04
—
泊松分布
这个我个人认为非常好用!还记得咱们之前讲独立性这块嘛,统计-2 概率P值,统计学意义泊松分布针对的就是独立性随机事件。
公式:
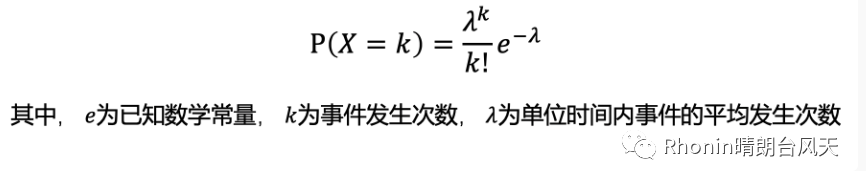
它不是求解整体发生率,而是求发生次数的概率,是计算累积分布概率。
还记得当样本足够小一切皆有可能这句话嘛,这个时候可以好好体会一下。
举个例子,在某个时间段内吃瓜的数学期望次数应该是5,那这个时间内吃6次及7次以上概率是1-61.6%=38.4%.大家特别留意一下标黄部分,当超过期望值后概率分布函数就开始降低了
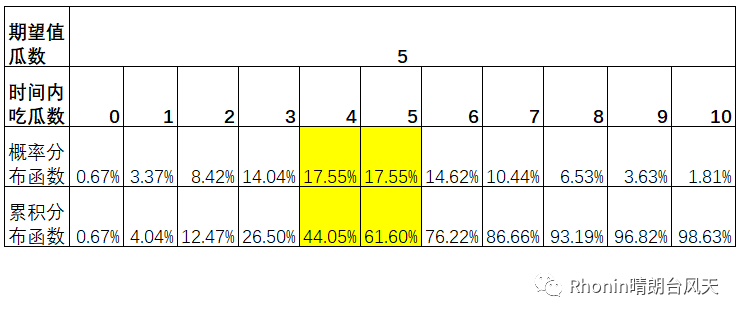
如果我们分别降低和增加样本量,对比看看统一均数的概率会发生什么变化?
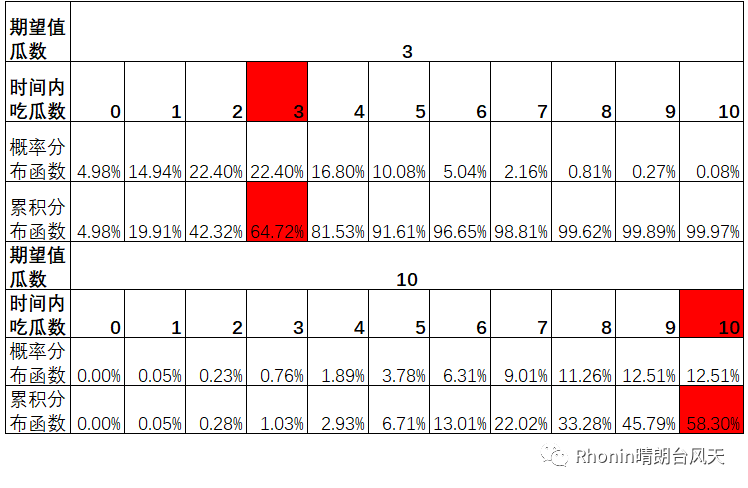
达到期望值3后还能再吃到瓜的概率是1-64.72%=35.28%,达到期望值3后还能再吃到瓜的概率是1-58.30%=41.7%,我们来进行一个对比:35.28%<38.4%<41.7%,说明当样本量越大,越能抵消随机性带来的误差,所以达到均值后再吃瓜的概率也会提升。购买保险的数学原理就是从这而来。同时,为了预防不测,我们还需要留有一些冗余。







