统计-2 概率P值，统计学意义

01

—

统计-1 统计与概率是门虐待学吗？
上篇我们尽管知道了真实世界里大多是没有边界不确定性的问题 ，但我们也还是希望能找到不确定性背后的规律在某种程度上去解决问题，于是我们把不确定性里关于能解决的随机性问题分类出来。

从这里开始，咱们就来拆解一下统计学是怎么解决不确定性里的随机问题。

随机也就意味着我们知道一件事儿可能发生的所有结果，但我们不知道的是每种结果发生的可能性，可我们可以通过比较可能性的大小来选择。那我们就需要想办法去衡量可能性，而概率P就是随机事件发生可能性大小的定量描述。

咱们上篇也说到概率论是基于严格证明推导，一定正确的数学对象，我想数学之所以美，是因为它用最简洁的描述揭示了世界规律，而且因为它一定正确所以提供了绝对的确定性。那么柯尔莫哥洛夫是怎样用公理来漂亮地描述概率论的？
这部分有点长和难，我们只要记住三条公理即可。引用吴军老师：“

首先，我们需要定义一个样本空间，它包含我们要讨论的随机事件所有可能的结果。【Rhonin:通俗可以理解成“总体”、“全集”】

接下来，我们需要定义一个集合，它包含我们所要讨论的所有随机事件【Rhonin:通俗可以理解成“样本”、“子集”】

接下来，我们需要定义一个函数（也被称为测度），使集合中任何一个随机事件对应一个数值。只要这个函数满足下面三个公理，它就被称为概率函数。【Rhonin:别被绕晕，就是概率P】

基于三个简单公理

这三个公理是：

公理一：任何事件的概率是在0和1之间（包含0与1）的一个实数。

公理二：样本空间的概率为1

公理三：如果两个随机事件A和B是互斥的，也就是说A发生的话B一定不会发生，那么，这件事发生的概率，就是A单独发生的概率，加上B单独发生的概率。这也被称为互斥事件的加法法则。

基于这样三个公理，整个概率论所有的定理，都可以推导出来。

定理一，互补事件的概率之和等于1。

定理二，不可能事件的概率为零。
自此，概率论才从一个根据经验总结出来的应用工具，变成了一个在逻辑上非常严密的数学分支。只有建立在公理化基础上的概率论，才站得住脚。”

至此，我抛出2个点：随机事件与随机事件之间的关系（本文第二部分），随机事件与总体的关系（本文第四部分）。

独立性，随机事件的相互关系

随机事件之间：要么具有独立性，要么具有非独立性。

独立性，举个扔硬币的例子，你已经连续扔了5次硬币都是正面，有人可能会觉得都已经扔了5次正面，那下次出现反面的才更合理，这叫“赌徒谬误"（也是大数定律经常被这样误解以为随机就是均匀，正确是大数定律不会对已经发生的情况进行补偿，而是利用大量的正常数据，削弱那部分异常数据的影响。）

也会有人觉得既然连续5次正面，应该趁热打铁，下次出现正面的可能性更高，这叫“热手谬误”。

相信大家都知道概率更大更小都不对，第六次扔硬币无论正反面概率仍然是50%，因为扔硬币是独立性事件，也就是说如果一个随机事件发生的结果不会对另一个随机事件的概率，那它们就是相互独立，反正就是非独立。确定独立还是非独立，才能正确分析和度量概率。这是先决条件。

概率P到底是怎么度量的？

度量概率的方法有三种——定义法、频率法、迭代法，它是逐步出现的。

1、定义法

对称性，是世界的普遍规律。所以，如果没有充分理由说明某件事的概率，就给予每个结果相同的概率。这就是定义法通过自然世界的对称性也就是等可能性来定义概率，如古典概率。

但现实生活中很多事情并不全都是等可能性的，所以就出现了频率法。

2、频率法

频率法就是说，只要数据量足够多，一个随机事件发生的频率就会无限接近它发生的概率。也就是大数定律，它是经过数学证明绝对正确的。依靠大量数据获得真相的思路，是现代统计学的基础。频率法，是用随机事件发生的频率来计算概率。

慢慢我们又发现还是有些事依旧解决不了，有些事没法试，比如我不可能跟男神告白100次来统计成功的概率，从长期看有些事是不断变化的，那它的概率也是不断变化的，比如我先和男神做个朋友培养下感情那我成功的概率是不是又提高了，有些事跟个体差异有关。

3、迭代法

迭代法就是说，先利用手头少量的数据做推测，甚至是主观猜测一件事儿的概率，然后再通过收集来的新数据，不断调整对这件事概率的估算。最常用的方法就叫作“贝叶斯”。迭代法，是用一种动态发展的、考虑个人差异的角度来度量概率。

三种方法是可以融合使用的。

误差从何而来？

频率法，是现代统计学的基础。大数定律在数学上证明了频率法的合理性。大家再回顾一下我们描述里有一句话【当数据量足够多】，这个足够多就显得很怪异了，到底多少才叫足够多呢？足够多不是一个静态数字，是一个无限的数学概念，一个动态趋势，类似“无穷大无穷小”。也就意味着，现实中做不到无限。理想与现实的差距导致了精度误差，也可以叫抽样误差。

因为无法获得足够多的数据，所以我们会在现实中设置一些条件随机抽样，通过对抽样的分析来推断理想中的总体。

大数定律：当样本量足够大，一切皆法自然。

小数现象：当样本量足够小，一切皆有可能。

好好体会以上两句话，样本量越小的样本，抽样误差越大。误差反映了数据的集中和离散趋势。误差越小，数据越集中，误差越大，数据越离散。如果误差太大，那我们的样本就也无法给出足够正确的结果。一般我们可以通过点估计和区间估计（这2个概念后解）推断结果，区间估计是一个更科学的方法。

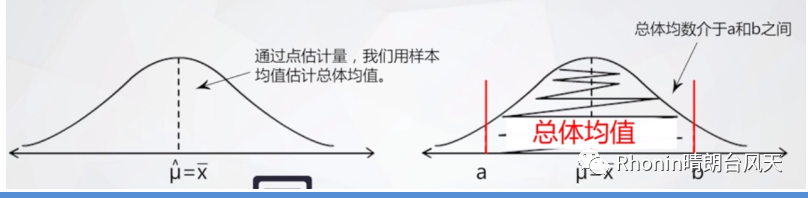
区间估计其实就是通过标准误（这个概念后解）来区分置信区间，也是衡量结果的可靠度，95%就是通用的。如果你的样本没有在95%的区间范围内，那就是属于小概率事件，一般可以认为不会发生。统计学就是基于小概率事件进行统计推断。

不够精确的总结

我理解下的统计学：

不确定性问题→提取随机性问题→随机可能性概率P→先判断是否独立→频率法度量概率P→现实做不到足够多数据量→现实与概念的误差（总体与样本均值差距）→区间估计衡量概率P可信度→小概率验证推断总体。

概率P是随机性问题的钥匙，也是统计学真正的目的，而抽样误差不可避免，所以需要那么多统计方法来推断概率P可靠性。

以上虽然不够精确，但核心意思应该表达了七八成。