NeurIPS 2020 | 基于图表示学习的缺失特征填充和标签预测模型

❝

论文标题 ｜ Handling Missing Data with Graph Representation Learning

论文来源 ｜ NeurIPS 2020

论文链接 ｜ https://arxiv.org/abs/2010.16418

源码链接 ｜ https://github.com/maxiaoba/GRAPE

❞

TL;DR

针对数据特征缺失的 feature imputation 和 label prediction 问题，论文提出了一种基于图的处理框架 GRAPE。GRAPE 基于图表示学习的方法来处理缺失特征填充和标签预测问题，主要思路是将观测样本点和特征类型作为二分图中的两种类型节点，其观测特征值作为边，按二分图建模即可：将特征填充问题转为边级别的预测任务，将标签预测问题转为节点级别的预测任务。实验部分在九个基准数据集中验证了 GRAPE 在缺失值填充任务中 MAE 可提高 20% 且在标签预测任务中提高 10%。

Problem Definition

给定 个数据点的 维特征 ，缺失值矩阵表示为 ， 表示对应数据点 的特征值不是缺失的。令 表示下游任务的标签且 表示标签是否已知。现需解决两个问题：

• 「feature imputation」：在 时预测缺失的特征值 ;
• 「label prediction」：在测试集中 时预测标签 ;

Algorithm/Model

论文中提出 GRAPE 框架如下图所示，主要思想是将缺失值问题转为二分图中节点和边级别的预测问题，然后利用 GNN 模型来解决图级别的任务。👍🏻

所以说大佬们的厉害之处就在于可以将本不相关的问题转化为自身领域相关的问题，然后利用自身擅长的方法来解决而且 thoughts 还显得那么 make sense  🤟🏻 不得不膜拜啊！🤙🏻

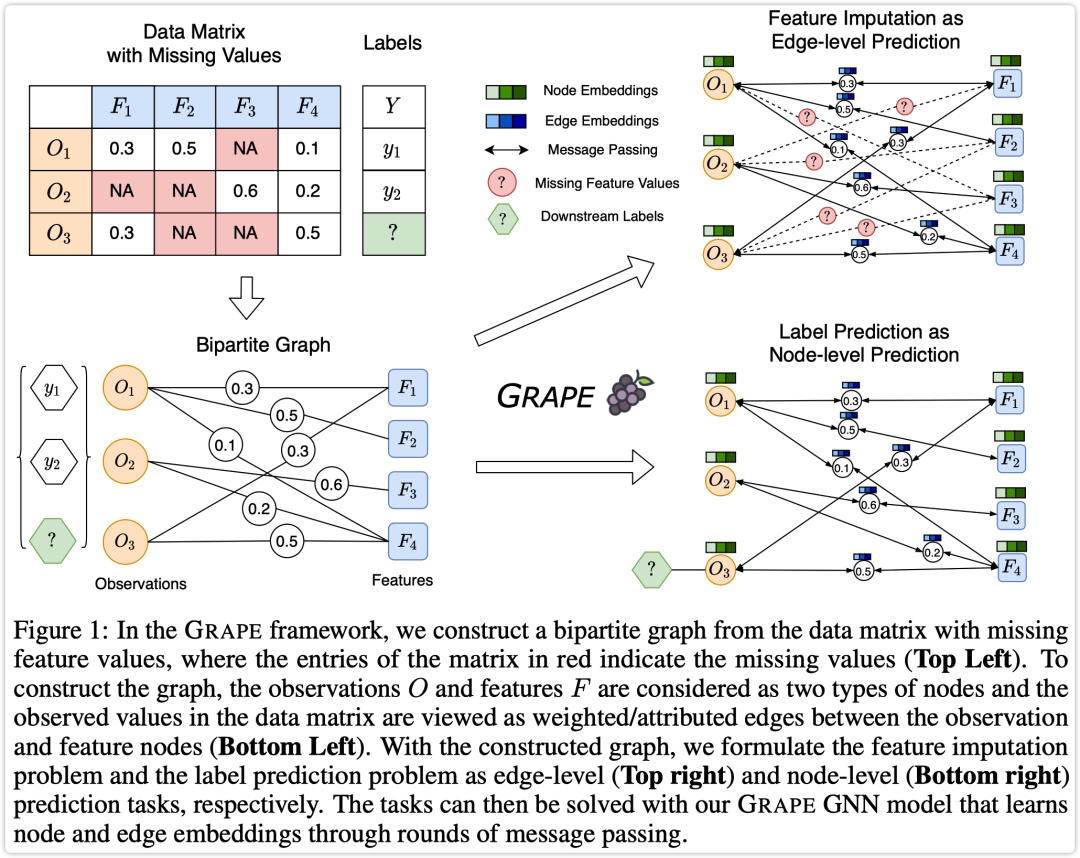
问题转化

给定特征矩阵 及其掩码矩阵 表示为无向二分图 ，其中节点 表示数据类型的顶点集合， 表示特征类型的顶点集合； 表示两种类型节点间存在的边集合 ，其中 表示对应特征值 ，如果为类别特征那么转为 one-hot 编码。 简化表示 表示特征矩阵 间关系， 表示图 节点间关系。

❝

此处 edge encoding 可能存在问题：如果数据中既存在连续特征又存在离散特征，那么会导致边向量的维度不同，如何处理？🤔

❞

对应两个任务如下：

• 「edge-level prediction」

  对于 预测边值 ，优化目标为最小化 和 距离，损失函数 MSE/Cross entropy；

• 「node-level prediction」

  对于 预测节点标签 ，优化目标为最小化 和 距离；

选择模型

论文中选用的是经典的 GraphSAGE 模型，详细介绍可以参考另一篇文章：NIPS 2017 | GraphSAGE：大规模图上的归纳表示学习模型

为了使 GraphSAGE 适应二分图中的缺失值预测问题，作者对其进行改进优化。

GRAPE GNN

给定二分图 ，首先将 edge embeddings 加入 GraphSAGE 中。对于 层 GNN，其输入为源节点node embedding 加上边 edge embedding 连接

其中 表示聚合函数， 为激活函数， 为训练权重， 为邻居节点。然后 node embedding 更新为

其中 为可训练权重。然后 edge embedding 更新为

其中 为可训练权重。

对应的 edge-level 预测为

对应的 node-level 预测为

其中 和 都是前馈神经网络 MLP。

node augmented

从上面的构图来看 都是没有特征的，会使模型难以区分不同类型的节点，所以论文中对两种类型的节点扩充 维特征：

edge dropout

为了防止过拟合，在训练时对二分图 中的边以概率 进行随机 dropout:

其中 是随机矩阵；

上述所有步骤如下图所示

Experiments

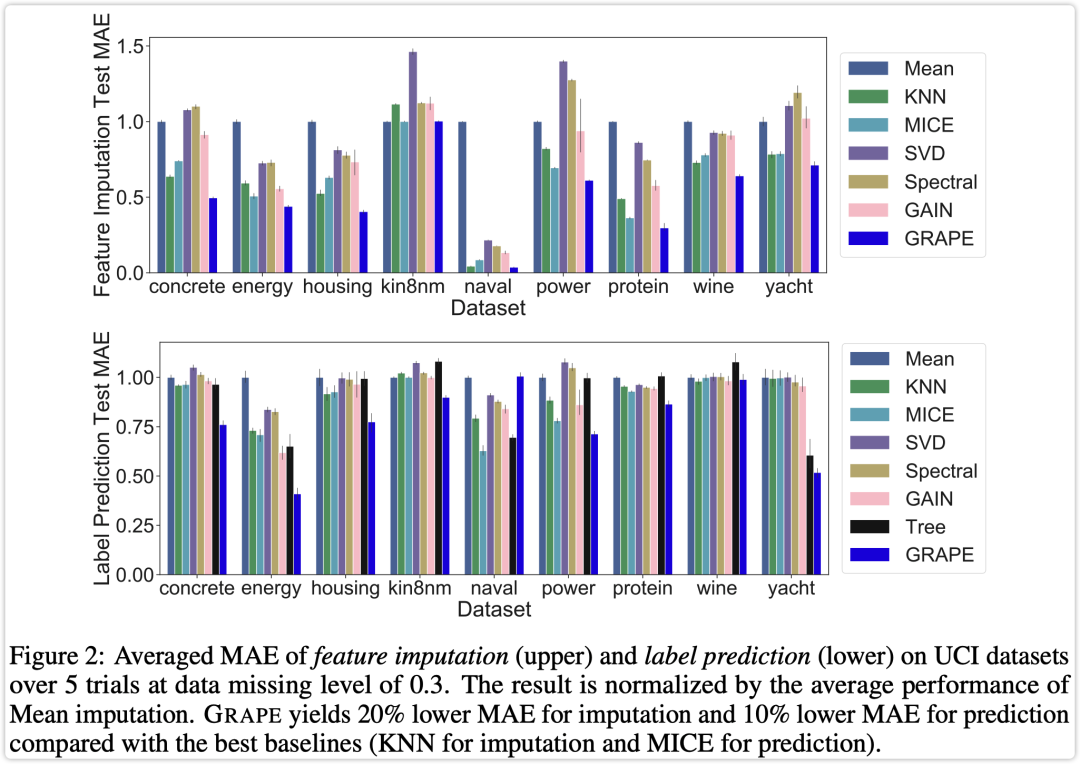
实验部分从 UCI 数据集中采用了 9 个数据集，对比实验中采用了 7 个 baselines，其结果如下

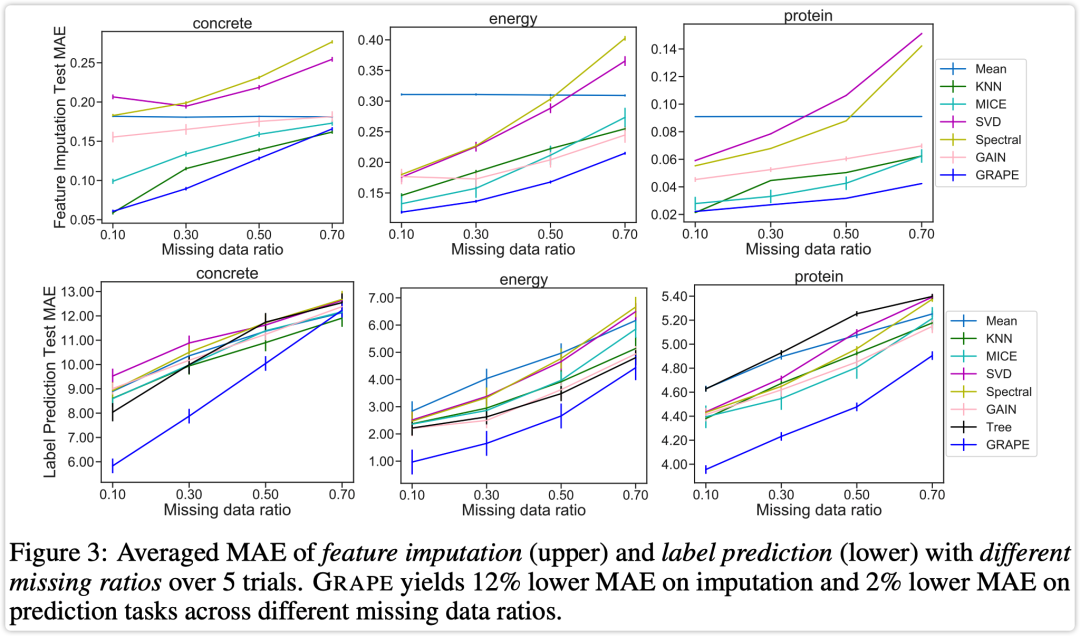
在不同缺失比例的数据集中测试结果如下

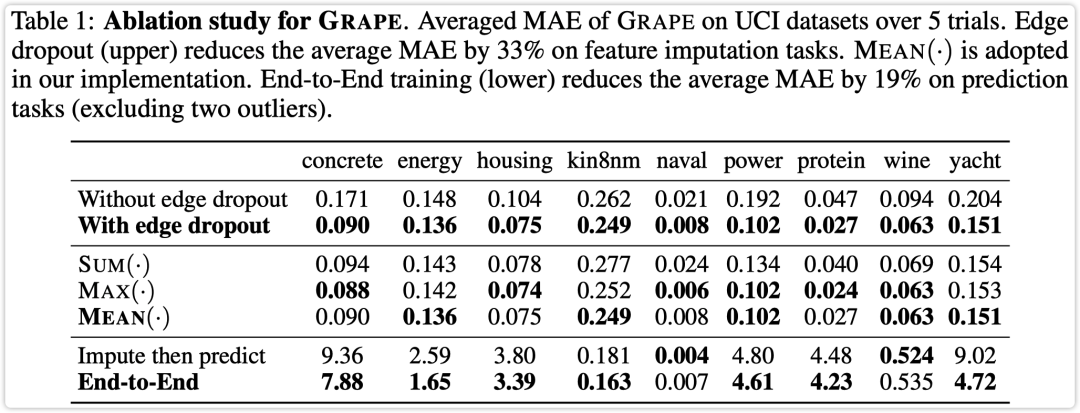
消融实验结果如下

整体而言 GRAPE 方法都优于其它模型，不愧是用了 GNN 的模型！

Thoughts

• 对缺失值填充问题提出了新的基于图的解决方案，即可以预测缺失值又可以预测标签，不愧是大佬 🤙🏻 想法就是这么具有开创性；
• Jure Leskovec 组的文章写的和故事一样通俗易懂，单纯地膜拜下没事看的陶冶情操 🌹
• 对于不同类型特征导致不同 edge encoding 维度的问题，看样子需要从源码看处理的 trick 了；

❝

推荐阅读

• ICML 2021 | 针对图神经网络的通用因果解释方法
  
• NeurIPS 2019 | 基于图自编码器的因果结构学习模型
  
• AGC：基于自适应图卷积的属性图聚类模型
  
• SNAPSKETCH：基于图表示学习的图流异常检测模型
  

❞