一.计算导数:
1.符号解
①显函数
D=diff(fx,x,n);
②隐函数
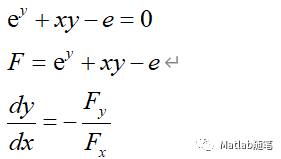
syms x y
F=exp(y)+x*y-exp(1);
D=-diff(F,y,1)/diff(F,x,1);
③参数方程
function result=diff_para(y,x,t,n)
% y,x:参数方程表达式
% t:参数方程符号自变量
% n:求导阶次
if n==1
result=diff(y,t)/diff(y,x);
else
result=diff_para(y,x,t,n-1)/diff(x,t);
end
end
2.数值解(针对离散数据)
原理:已有离散数据,用插值多项式求出其近似函数,然后计算离散点处的导数值
function d=poly_str(xd,yd,xi,N)
% xd,yd:离散数据
% xi:数值求导点
% N:求导阶次
L=length(xd)-1;
p=polyfit(xd,yd,L);
for k=1:N
p=polyder(p);
end
d=polyval(p,xi);
end
3.例子:计算sin(x)的高阶导数
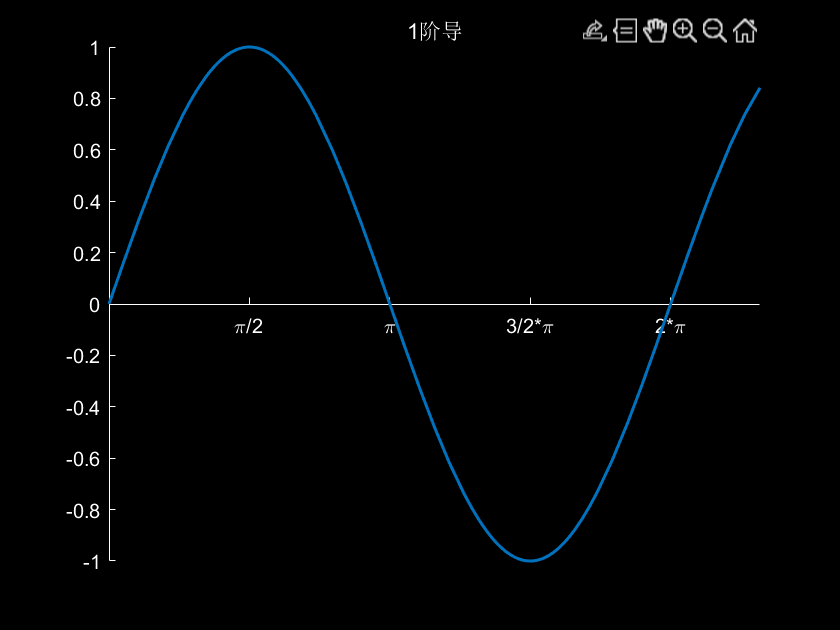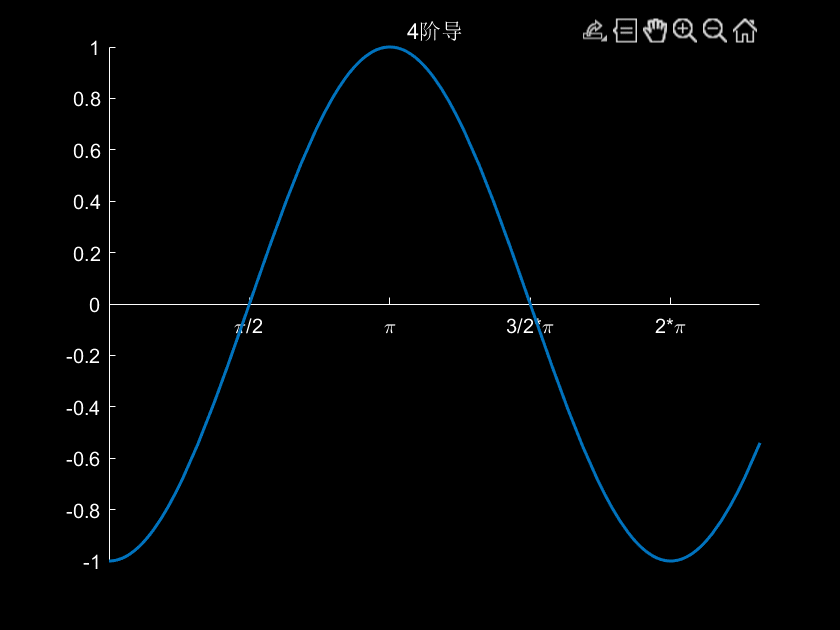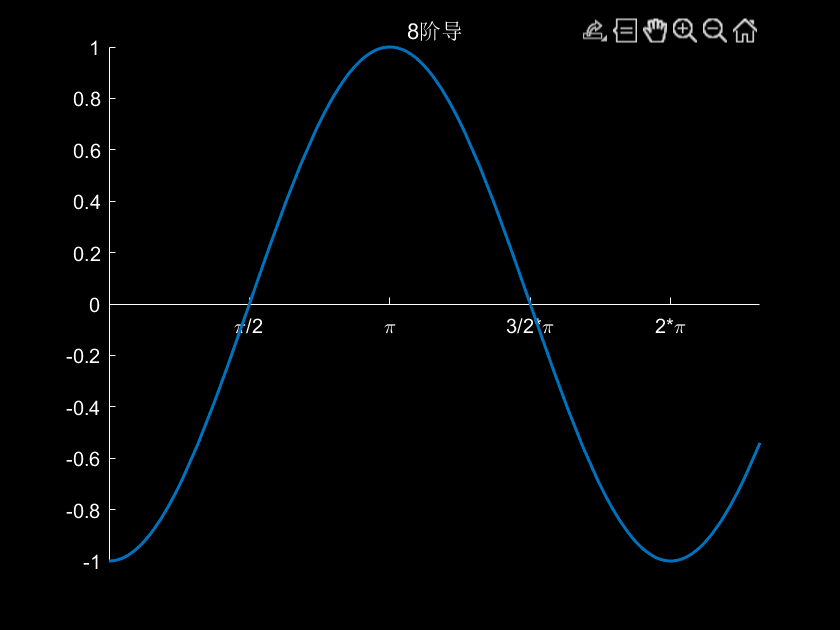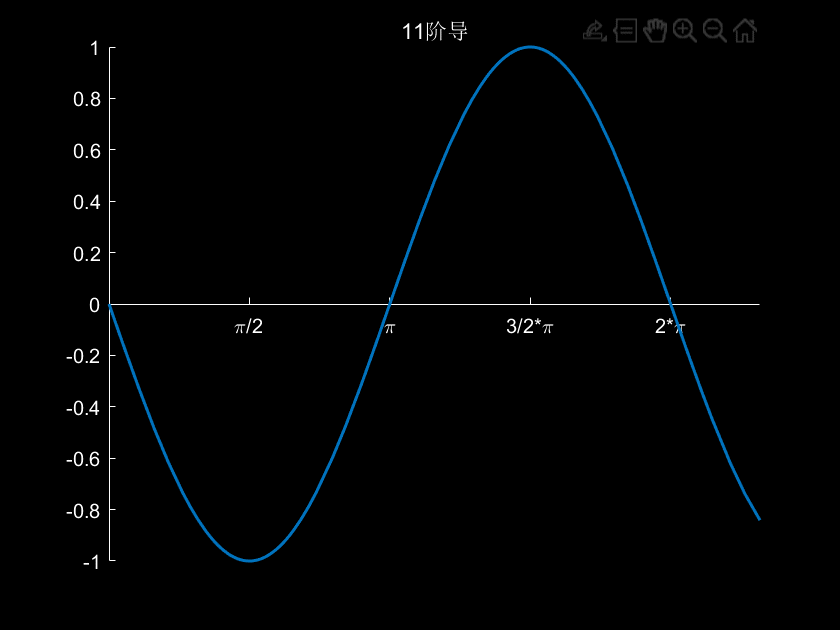
fig=figure;
fig.Color=[0 0 0];
syms x
f=sin(x);
for i=1:11
fplot(f,[0,2*pi+1],'LineWidth',1.5);
ax=gca;
ax.XColor=[1,1,1];
ax.YColor=[1,1,1];
ax.Color=[0,0,0];
ax.Box='off';
ax.XAxisLocation='origin';
ax.YAxisLocation='origin';
xticks(0:pi/2:2*pi);
xticklabels({'0','\pi/2','\pi','3/2*\pi','2*\pi'});
ylim([-1,1]);
title([num2str(i),'阶导'],'Color',[1 1 1]);
pause(0.2);
d=diff(f,x,1);
f=d;
frame = getframe(fig);
im = frame2im(frame);
[A,map] = rgb2ind(im,256);
if i == 1
imwrite(A,map,'1.gif','gif','LoopCount',Inf,'DelayTime',0.5);
else
imwrite(A,map,'1.gif','gif','WriteMode','append','DelayTime',0.5);
end
end
二.计算微分:
syms x
y=sin(x);
dy=[char(diff(y,x,1)),'dx'];
三.泰勒公式:
1.函数
% x,y:数据点坐标
% x0:展开位置
% i:展开至i-1阶
r=taylor(y,x,x0,'Order',i);
2.工具箱
taylortool
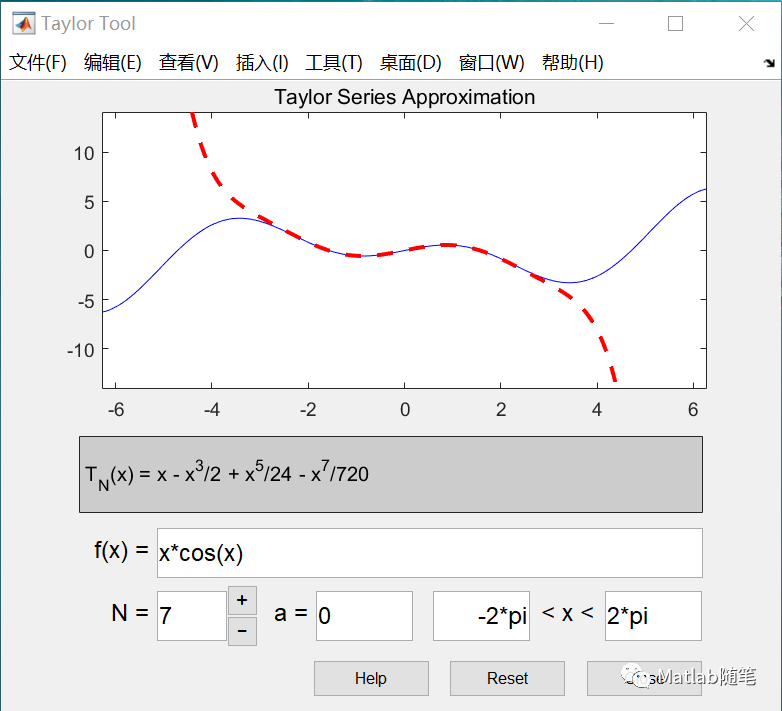
3.例子:演示y=sin(x)在x=0处泰勒公式展开情况
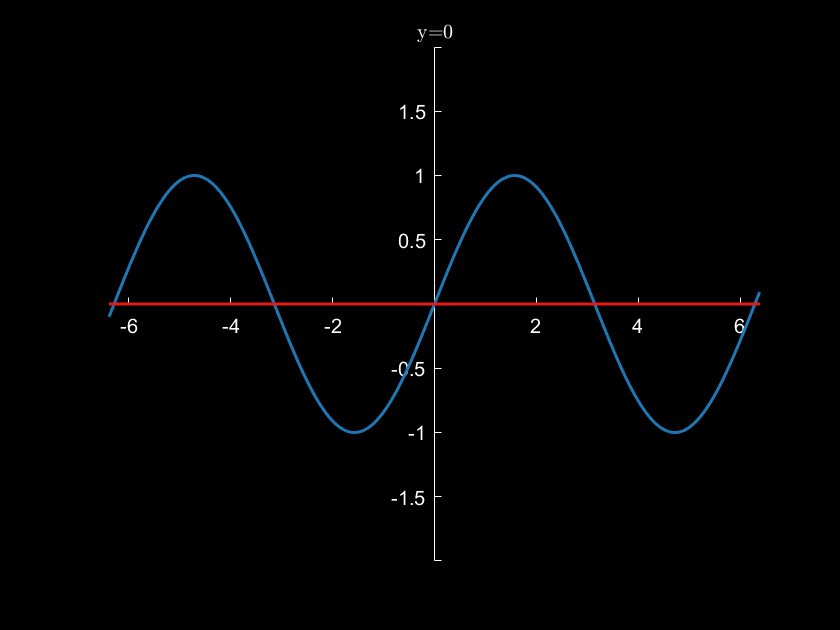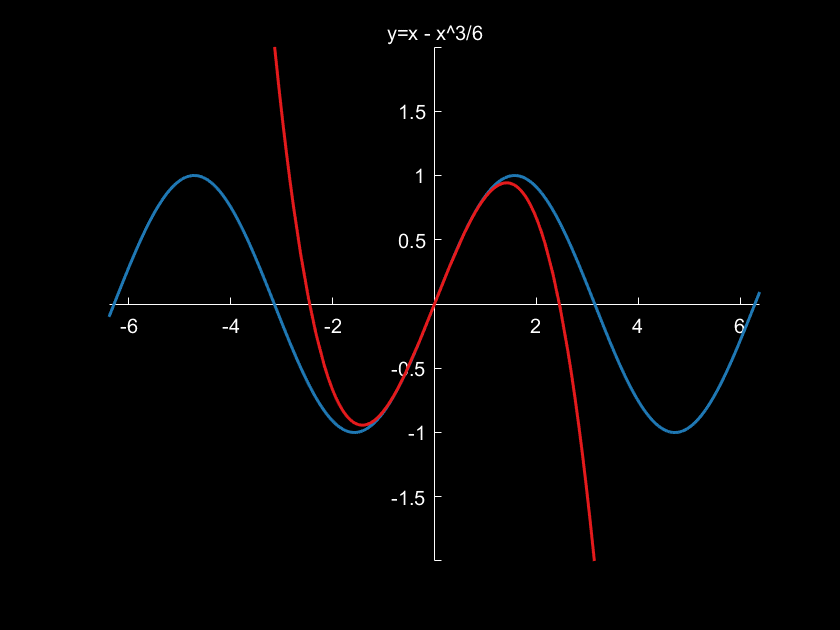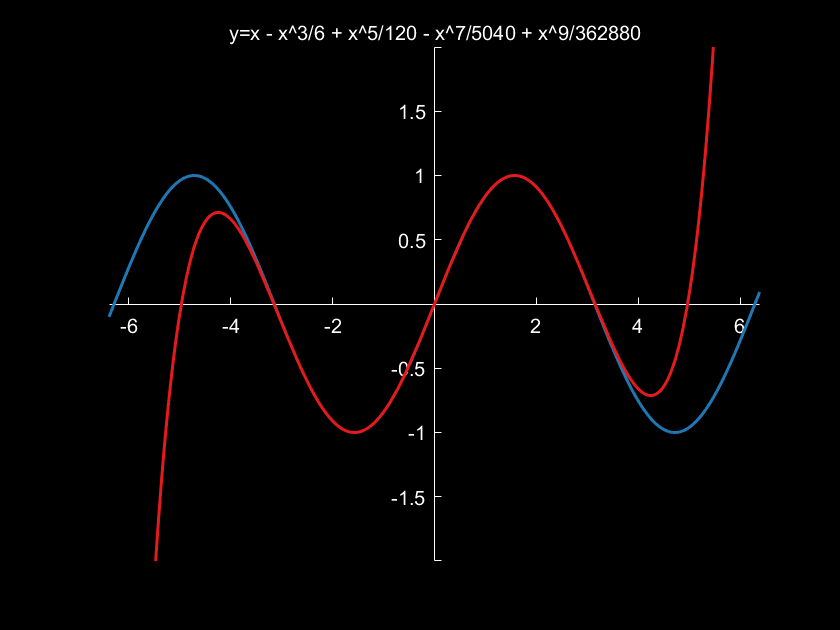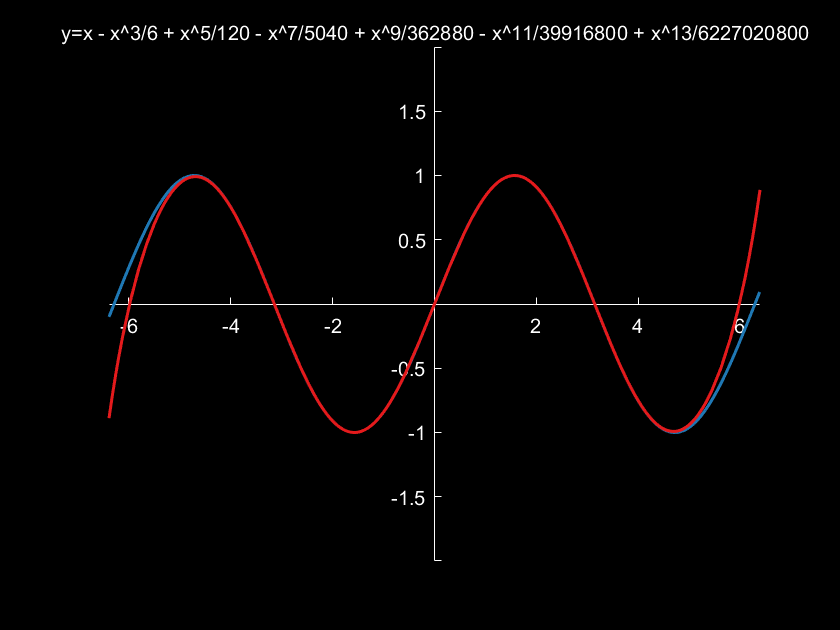
x1=-2*pi-0.1:0.01:2*pi+0.1;
y1=sin(x1);
fig=figure;
fig.Color=[0 0 0];
p1=plot(x1,y1,'LineWidth',1.5,'Color',[0.1216 0.4706 0.7059]);
ylim([-2,2]);
xlim([-2*pi-0.1,2*pi+0.1]);
hold on;
syms x
y=sin(x);
for i=1:14
r=taylor(y,x,0,'Order',i);
p2=fplot(r,[-2*pi-0.1,2*pi+0.1],'LineWidth',1.5,'Color',[0.8941 0.102 0.1098]);
ax=gca;
ax.XColor=[1,1,1];
ax.YColor=[1,1,1];
ax.Color=[0,0,0];
ax.Box='off';
ax.XAxisLocation='origin';
ax.YAxisLocation='origin';
title(['y=',char(r)],'Interpreter','latex','FontSize',10,'Color',[1,1,1]);
frame = getframe(fig);
im = frame2im(frame);
[A,map] = rgb2ind(im,256);
if i == 1
imwrite(A,map,'2.gif','gif','LoopCount',Inf,'DelayTime',0.5);
else
imwrite(A,map,'2.gif','gif','WriteMode','append','DelayTime',0.5);
end
pause(0.2);
delete(p2);
end
参考资料:《基于MATLAB的高等问题求解》
文章转载自不糊涂录,如果涉嫌侵权,请发送邮件至:contact@modb.pro进行举报,并提供相关证据,一经查实,墨天轮将立刻删除相关内容。






