字节面试题：分糖果问题

大家好，我是程序员学长。

今天我们来聊一聊面试字节时遇到的一道算法题：分糖果问题。

如果喜欢，记得点个关注哦~

分糖果1

问题描述

给定一个偶数长度的整数数组，数组中不同的数字代表着不同种类的糖果。每个数字代表一个糖果，现在你需要把这些糖果平均分配给一个弟弟和一个妹妹，返回妹妹可以获得的最大的糖果的种类数。

示例：

输入: candies = [2,2,3,3,4,4]

输出: 3

解析: 数组中有三种不同的数字2、3、4，代表了三种不同种类的糖果，每一种都有两个。在这种情况下，最优的分配方案是，妹妹获得[2,3,4]，弟弟也获得[2,3,4]。这样使得妹妹获得的糖果种类数最多。

分析问题

根据题目要求，需要平均分配糖果给弟弟和妹妹，所以妹妹能分配到的糖果数量为n/2。最好的情况是妹妹得到的n/2个糖果是属于不同种类的，也就是说妹妹可以得到的最大的糖果种类数是n/2。此外，如果数组中糖果的种类数小于n/2时，为了使妹妹得到的糖果种类数达到最大，我们会将数组中不同种类的糖果都分配给妹妹。因此，在这种情况下，妹妹能获得的不同种类的糖果数量等于给定数组中糖果的种类数。

现在我们就把问题转化成如何求出数组中糖果的种类数，假设为count。那么分配给妹妹的最大糖果种类数就是min(n/2,count)。下面我们来看一下如何求出数组中糖果的种类数，最直观的想法就是遍历给定的数组，然后将元素放入一个集合Set中，利用集合Set能去重的特性，来求出数组中糖果的种类的个数。

def distributeCandies(candies):
    candies_set=set()
    #遍历数组
    for canday in candies:
        #为了获得不同种类的糖果数
        candies_set.add(canday)
        
    return min(len(candies)/2, len(candies_set))

candies = [1,1,2,2,3,3]
print(distributeCandies(candies))

分糖果2

问题描述

我们现在有candies个糖果，打算把他们分配给排好队的n个小朋友。我们采取下面这种分配策略。给第一个小朋友1颗糖果，第二个小朋友2颗，依此类推，直到给最后一个小朋友n颗糖果。然后，我们再回到队伍的起点，给第一个小朋友n + 1颗糖果，第二个小朋友n + 2颗，依此类推，直到给最后一个小朋友2 * n颗糖果。重复上述过程（每次都比上一次多给出一颗糖果，当到达队伍终点后再次从队伍起点开始），直到我们分完所有的糖果。注意，就算我们手中的剩下糖果数不够（不比前一次发出的糖果多），这些糖果也会全部发给当前的小朋友。返回一个长度为n、元素之和为candies的数组，以表示糖果的最终分发情况（即 ans[i] 表示第 i 个小朋友分到的糖果数）。

示例：

输入：candies = 9, n= 3

输出：

解释：第一次，ans[0] += 1，数组变为 [1,0,0,0]。第二次，ans[1] += 2，数组变为 [1,2,0,0]。第三次，ans[2] += 3，数组变为 [1,2,3,0]。第四次，ans[3] += 3（因为此时只剩下 3 颗糖果），最终数组变为 [1,2,3,3]。

分析问题

拿到这个问题最直观的想法就是不断的把糖果分配给n个小朋友，直到把糖果分配完为止。下面我们来看一下代码如何实现。

def distributeCandies(candies,n):
    ans=[0]*n
    i=0

    while candies>0:
        #分配给哪个人了
        index=i%n
        ans[index]=ans[index]+min(i+1,candies)
        candies=candies-min(i+1,candies)
        i=i+1

    return ans

candies=9
n=4
print(distributeCandies(candies,n))

分糖果3

问题描述

现在有一群孩子做游戏，请你根据游戏得分来发糖果，要求如下：

1. 每个孩子不管得分多少，起码分到一个糖果。

2. 任意两个相邻的孩子之间，得分较多的孩子必须拿多一些糖果。(若相同则无此限制)

给定一个数组arr代表得分数组，那你根据规则分配糖果最少需要多少颗呢？

分析问题

首先，我们可以把题目的第二条规则拆分来看一下。对于任意相邻的孩子之间，我们可以拆分为左孩子和右孩子。

1. 左规则：当左孩子ratings[i-1]<ratings[i]时，当前孩子i的糖果数量要比它的左孩子i-1的多。
2. 右规则：当右孩子ratings[i+1]<ratings[i]时，当前孩子i的糖果数量要比它的右孩子i+1的多。

我们通过遍历两遍数组，分别求出每个孩子在满足左规则和右规则时，最少需要的糖果数量left、right。那么每个孩子最终分得的糖果数量就为这两个值left、right的最大值，即max(left,right)。下面我们来看一下代码实现。

def candy_count(ratings):
        n = len(ratings)
        # 用来保存满足左规则所需要的最少的糖果数
        left = [1] * n

        for i in range(1, n):
            if ratings[i] > ratings[i - 1]:
                left[i] = left[i - 1] + 1


        right = result = max(left[n-1],1)
        for i in range(n - 2, -1, -1):
            if ratings[i] > ratings[i + 1]:
                right += 1
            else:
                right = 1
            result += max(left[i], right)

        return result

s=[1,3,5,3,2,1]
print(candy_count(s))

我们来看一下算法的复杂度。

1. 时间复杂度：O(n)，其中n是孩子的数量。我们需要遍历两遍数组来求出满足规则所需要的最少糖果数。
2. 空间复杂度：O(n)。

那我们有什么方法可以来降低空间复杂度吗？

优化

根据题目要求，我们在分配糖果时要尽量少分配，并且每个孩子起码要分配到1个糖果。

我们从左到右遍历每一个孩子，记前一个孩子分得的糖果数量为pre。

1. 如果当前孩子比上一个孩子的得分要高，说明我们目前处于最近的递增序列中，所以需要给该孩子分配pre+1个糖果。
2. 如果当前孩子和上一个孩子的得分相同，我们就分配给一个糖果，这样不违反规则。
3. 如果当前孩子比上一个孩子的得分要低，我们就给当前孩子分配一个糖果。同时，为了保证分配的糖果数量还满足条件，我们需要给该孩子所在的递减序列中的其它孩子再多分配一个糖果（这里可能不太好理解，我们通过一个例子来说明），所以我们需要一个变量dec来记录递减序列的长度。这里有一点需要注意，当递减序列长度和上一个递增序列长度相同时，我们需要把最近的递增序列的最后一个孩子并入到递减序列中。

我们来具体分析一个例子。假设有5个孩子，他们的得分别是1、3、5、3、2、1。

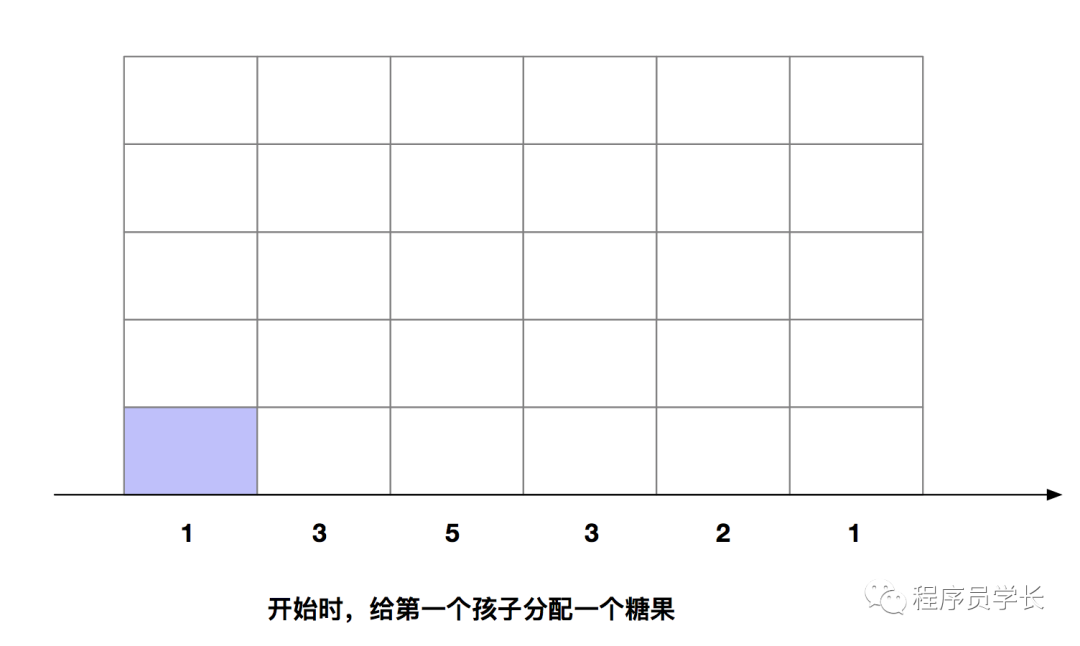
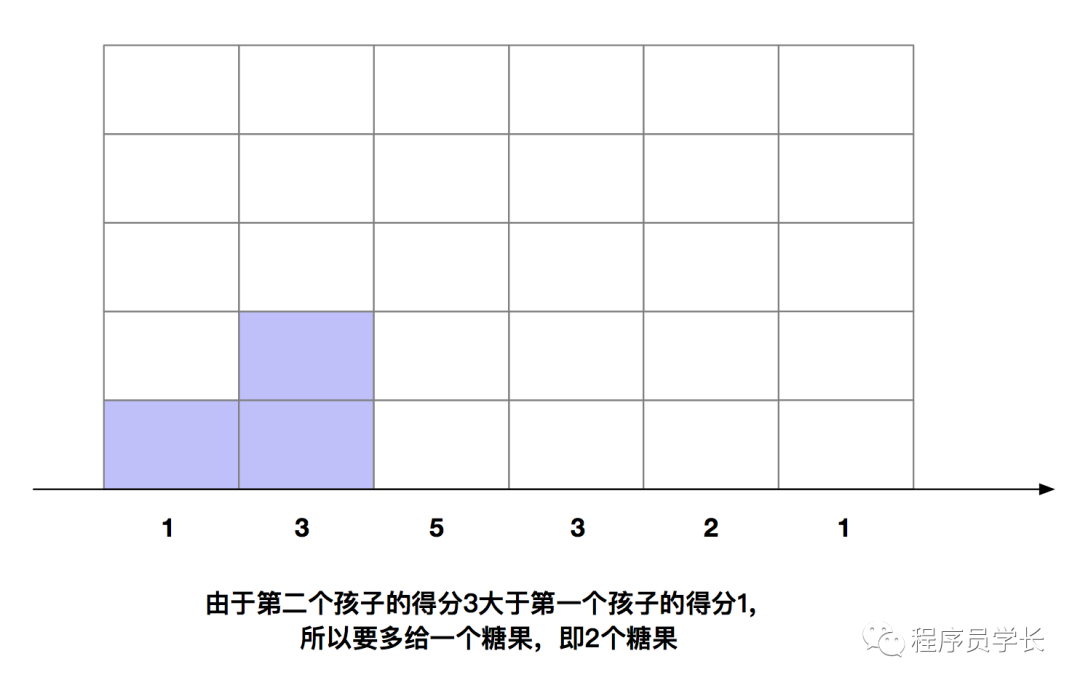
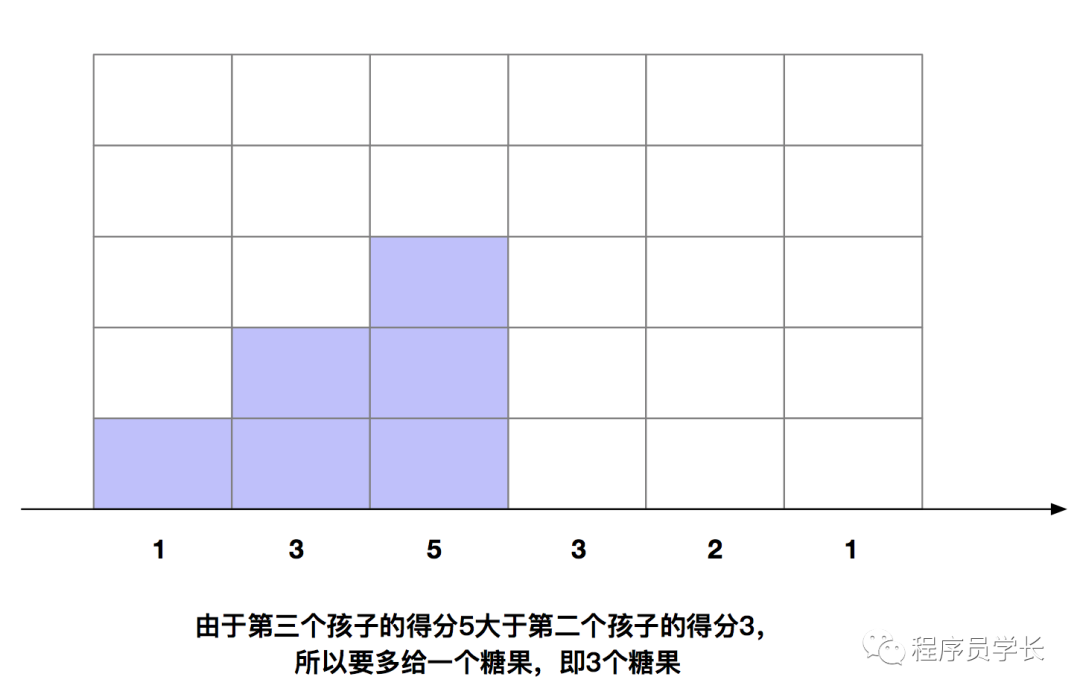
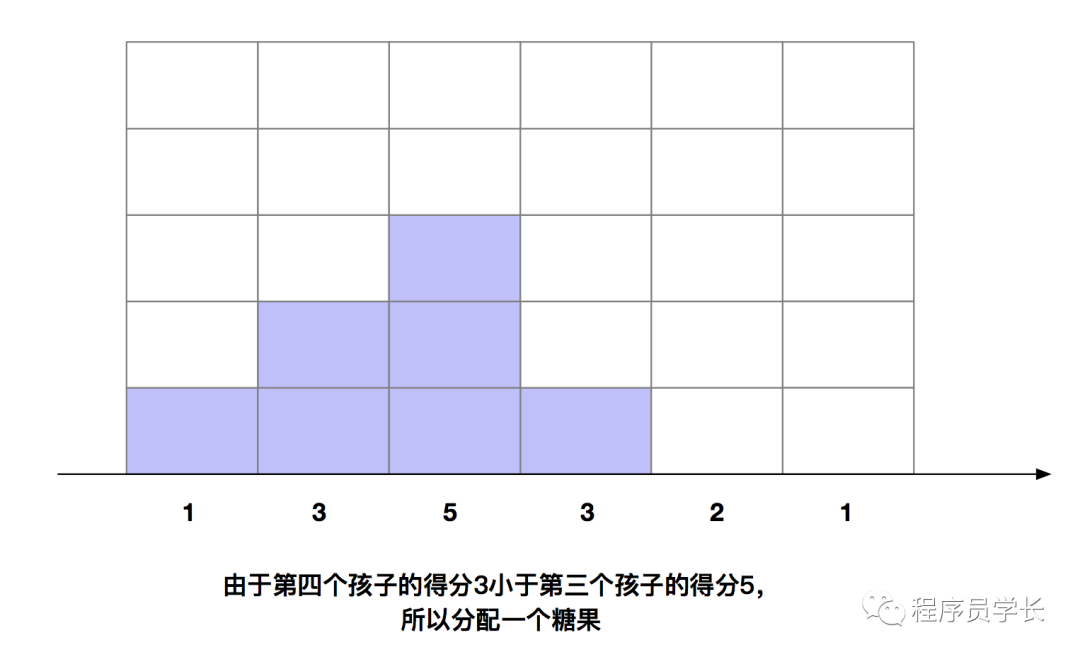
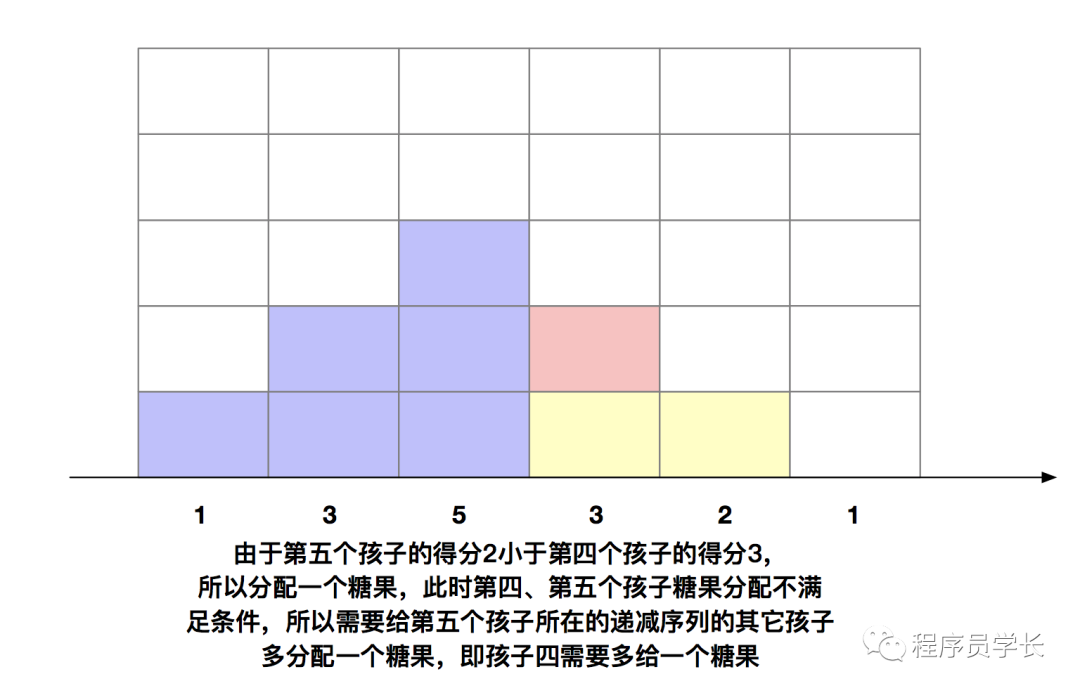
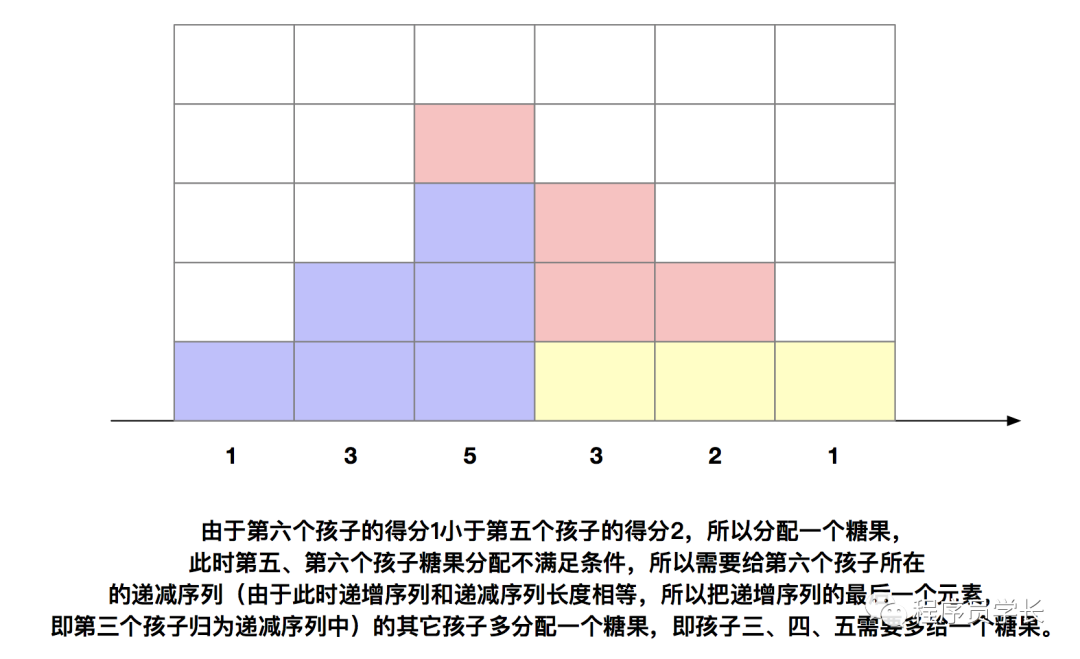
下面我们来看一下代码如何实现。

def candy_count(ratings):
    n = len(ratings)
    ret = 1
    #递增序列长度
    inc = 1
    #递减序列长度
    dec = 0
    #前一个孩子的糖果数
    pre = 1

    for i in range(1, n):
        if ratings[i] >ratings[i - 1]:
            dec = 0
            pre = pre + 1
            ret = ret + pre
            inc = pre
        elif ratings[i] == ratings[i-1]:
            dec = 0
            pre = 1
            ret = ret + pre
            inc = 1
        else:
            dec += 1
            if dec == inc:
                dec += 1
            ret += dec
            pre = 1

    return ret

s=[1,3,5,3,2,1]
print(candy_count(s))

我们来看一下算法的复杂度。

1. 时间复杂度：O(n)。
2. 空间复杂度：O(1)。

最后

到此为止，我们就把分糖果问题聊完了。如果喜欢，记得给个三连吧。

你知道的越多，你的思维越开阔。我们下期再见。