多项式贝叶斯原理及实现备忘

小张的科学日记 2020-11-18

685

帮朋友看了下贝叶斯的一个问题，就顺便研究了一下，正好这两天挂了两家医院，也能抽半上午的时间写一下做个备忘，去年某个时间看了下最大流最小切，没有做备忘，现在对着一张草图欲哭无泪，所以还是做做备忘，免得白费时间。

黑人是我有限生命里为数不多的乐趣，用黑人兄弟举个例子，我现在有一堆样本，其中非洲人分类里90%是黑人，10%是白人，欧洲90%是白人，10%黑人，那我看到一个黑人时我就能确认他来自非洲的概率为90%。

这里做了粗浅的假设，欧洲怎么可能10%黑人呢

贝叶斯定理

现在假设我们准备好贝叶斯定理推导的所有条件了

p(AB) = p(BA)

p(AB) = p(A)p(A|B)

p(BA) = p(B)P(B|A)

p(A)p(A|B) = p(B)p(B|A)

p(A|B) = p(B)p(B|A)/p(A)

求出当B条件下A的概率

朴素贝叶斯-多项式

假设概率分布满足多项分布，擅长分类型变量，多用于分本分类，借网图

训练阶段：

预测阶段：

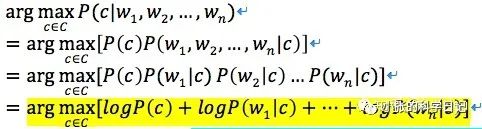
每一个p(w|c)都很小，直接按照定理相乘就向下溢出了，所以对数相加

代码实现

# 二分类，情感分析，简单改改就是多分类
# 可以看出训练过程就是求出每个类别的概率，以及类别中的特征的概率
# 将这俩保存下来就是训练出的模型，后续可以重复使用
def trainNB0(trainMatrix, trainCategory):
    numTrainDocs = len(trainMatrix)
    numWords = len(trainMatrix[0])
    pAbusive = sum(trainCategory)/float(numTrainDocs)
    # 拉普拉斯平滑，可能几千个特征词，太多了，很多0概率
    p0Num = np.ones(numWords);
    p1Num = np.ones(numWords);
    p0Denom = 2.0; 
    p1Denom = 2.0                        #change to 2.0
    for i in range(numTrainDocs):
        if trainCategory[i] == 1:
            p1Num += trainMatrix[i]
            p1Denom += sum(trainMatrix[i])
        else:
            p0Num += trainMatrix[i]
            p0Denom += sum(trainMatrix[i])
    p1Vect = np.log(p1Num/p1Denom)          #change to np.log()
    p0Vect = np.log(p0Num/p0Denom)          #change to np.log()
    return p0Vect, p1Vect, pAbusive
    
# 预测过程，就是计算条件概率，    
# 多分类，求出最大的概率
def classifyNB(vec2Classify, p0Vec, p1Vec, pClass1):
    p1 = sum(vec2Classify * p1Vec) + np.log(pClass1)    #element-wise mult
    p0 = sum(vec2Classify * p0Vec) + np.log(1.0 - pClass1)
    if p1 > p0:
        return 1
    else:
        return 0

数据库

文章转载自小张的科学日记，如果涉嫌侵权，请发送邮件至：contact@modb.pro进行举报，并提供相关证据，一经查实，墨天轮将立刻删除相关内容。

多项式贝叶斯原理及实现备忘

评论