在上篇《十分钟成为 Contributor 系列 | 为 Cascades Planner 添加优化规则》中,我们简单介绍了 Cascades 的相关背景知识,本文将为大家深入介绍 TiDB 新的优化器——Cascades Planner 的框架及原理。
TiDB 当前优化器简介
关系型数据库中查询优化器的作用是为一个 SQL 在合理的开销内产生一个合适的查询计划,TiDB 源码阅读系列文章(六)Select 语句概览 中介绍过 TiDB 当前优化器的基本组成,TiDB 当前的优化器将优化过程主要分为逻辑优化(Logical Optimize)和物理优化(Physical Optimize)两个阶段。逻辑优化是将一棵逻辑算子树(LogicalPlan Tree)进行逻辑等价的变化,最后的结果是一棵更优的逻辑算子树;而物理优化则是将一棵逻辑算子树转换成一棵物理算子树(PhysicalPlan Tree)。这棵物理算子树就是我们说的物理执行计划,将交由 TiDB 执行引擎去完成后续的 SQL 执行过程。
逻辑优化
select b from t where a > 1,其中
a是
int类型的主键,我们最终会产生这样一个物理执行计划:
TableScan(table: t, range:(1, inf]) -> TableReader(a, b) -> Projection(b)
ab两列,也就是说 TiDB 会从 TiKV 中读取两列内容,但最终自己却只需要其中第一列。这个问题背后的原因是:优化器先进行列裁剪,再谓词下推,但是谓词下推之后,有可能列剪裁可以再次生效,而这个可能生效的列剪裁在现在优化器中无法被执行了,导致 TiDB 从 TiKV 多读取了一列数据,增加了 SQL 执行时的网络 IO 使用量。
物理优化
在 TiDB 中,物理优化不仅仅是选择物理算子,还完成了算子下推 TiKV 的任务,例如将 Aggregation 算子分裂成 FinalMode 和 PartialMode 两部分,并将 PartialMode 的 Aggregation 下推到 TiKV Coprocessor 中执行,具体可以参考 TiDB 源码阅读系列文章(二十二)Hash Aggregation。
对于 Selection 算子,由于 Selection 在逻辑优化阶段被下推到 DataSource 中,因此在物理优化阶段中,如果 Selection 中有过滤条件不能转换成扫描的 Range 条件,就会产生一个 Coprocessor 层的 Selection。 对于 Limit、TopN 以及 Aggregation 算子,当且仅当它们的子节点是 DataSource 的时候,才允许被下推。
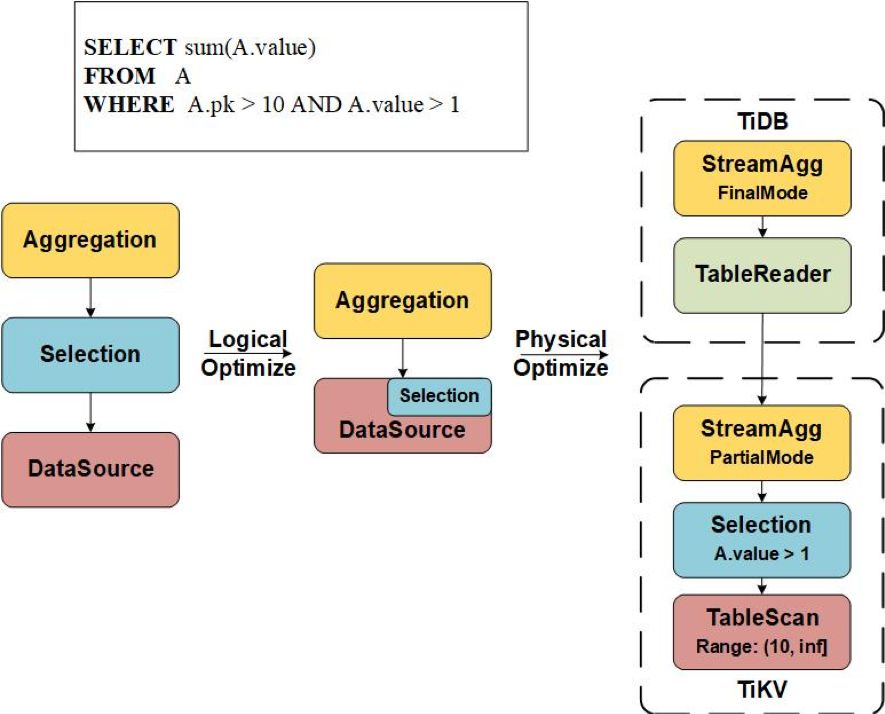
A.pk > 10会转换为主键的范围条件,而
A.value > 1则会产生一个 TiKV 层的 Selection。
算子下推逻辑过于简单,除了 Selection 之外只允许下推一个算子,难以应对未来添加的新的下推算子(例如 Projection 等),同时也没法针对某些特殊场景进行灵活地算子下推。 扩展性差:难以扩展支持其他的存储引擎,并实现相应的算子下推,例如 TiFlash(一个尚未开源的列存引擎)。 难以添加针对特殊数据源的优化规则,优化器的搜索空间进一步被限制。
The Volcano/Cascades Optimizer
The Volcano Optimizer Generator
Cascades Optmizer
Memo
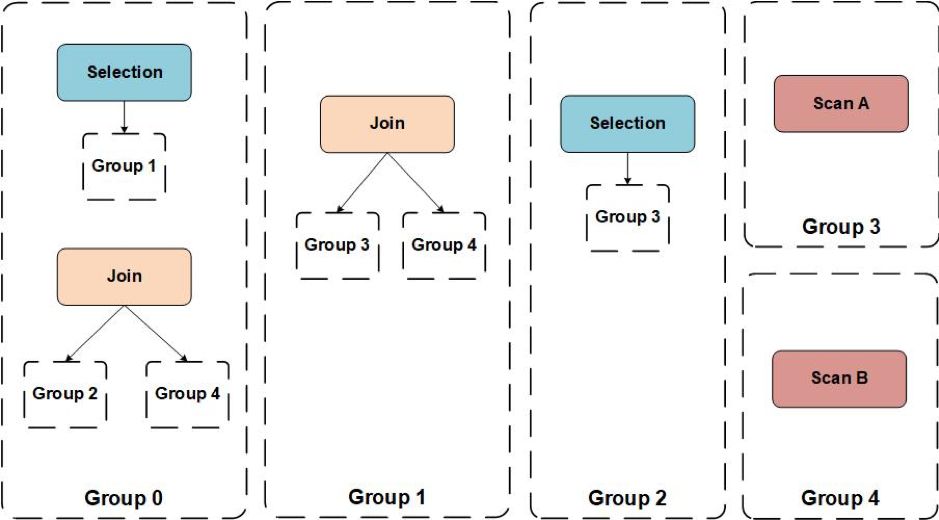
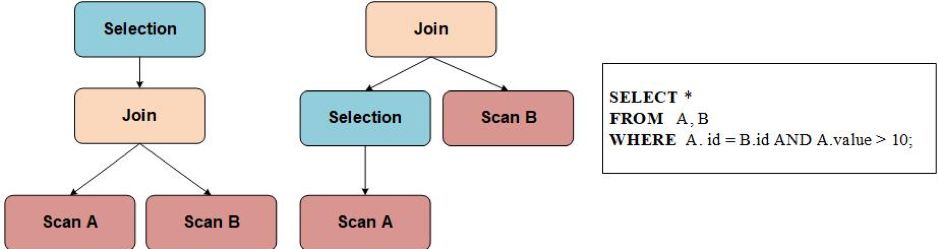
Cascades Optimizer 在搜索的过程中,其搜索的空间是一个关系代数算子树所组成的森林,而保存这个森林的数据结构就是 Memo。Memo 中两个最基本的概念就是 Expression Group(下文简称 Group) 以及 Group Expression(对应关系代数算子)。每个 Group 中保存的是逻辑等价的 Group Expression,而 Group Expression 的子节点是由 Group 组成。下图是由五个 Group 组成的 Memo:
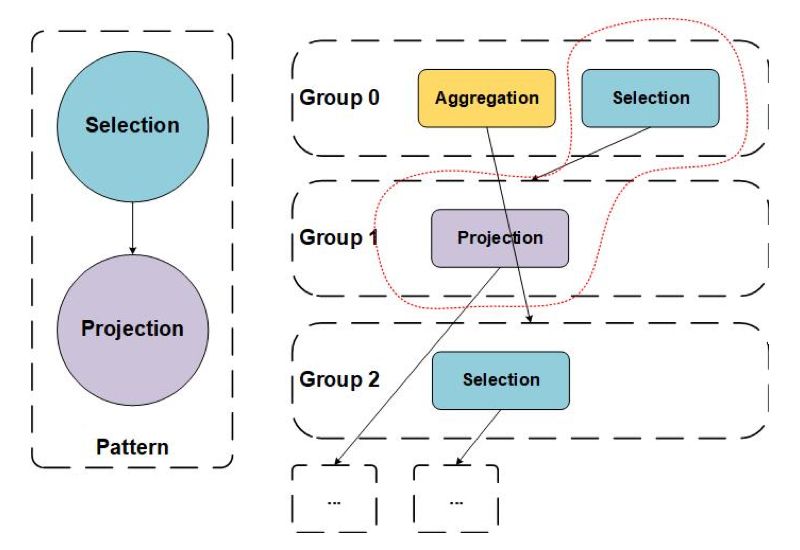
Rule
Selection->Projection的 Pattern,并在右侧 Memo 中红色虚线内出现了匹配的 Group Expression。
Searching Algorithm
TiDB Cascades Planner 的设计
优化规则易于实现,通过实现几个简单的接口来定义优化规则。 优化规则易于扩展,我们不需要再考虑优化规则的执行顺序。 优化规则可以反复应用,增大优化器的搜索空间。 对于不一定更优的优化规则,可以通过 Cost 来选取结果。 算子下推存储层更加灵活,方便未来扩展新的下推算子。 使 TiDB 可以更容易地接入其他的存储或者计算引擎,例如 TiFlash。 为 TiDB 的优化器能力分级,不同复杂程度的查询可以选用不同的优化等级。
基本数据结构
LogicalPlan的封装,与
LogicalPlan不同的是,GroupExpr 的子节点不再是
LogicalPlan,而是 Group:
type GroupExpr struct {
ExprNode plannercore.LogicalPlan
Children []*Group
Group *Group
...
}
type Group struct {
Equivalents *list.List
ImplMap map[string]Implementation
Prop *property.LogicalProperty
EngineType EngineType
}
type Operand int
const (
OperandAny Operand = iota
OperandJoin
OperandAggregation
OperandProjection
...
type Pattern struct {
Operand
Children []*Pattern
}
Transformation
GetPattern()
方法获取这个变换规则所需要匹配的一个 Pattern。由于 Pattern 只能描述算子的类型,不能描述 LogicalPlan 内部的内容约束,因此通过 Match()
方法可以判断更细节的匹配条件。例如 Pattern 只能描述我们想要一个 Join 类型的算子,但是却没法描述这个 Join 应该是 InnerJoin 或者是 LeftOuterJoin,这类条件就需要在Match()
中进行判断。OnTransform()
方法中定义了变换规则的具体内容,返回的内容分别是新的 GroupExpr,是否删除旧的GroupExpr
,是否删除旧的 Group 中所有的GroupExpr
。
// Transformation defines the interface for the transformation rules.
type Transformation interface {
GetPattern() *memo.Pattern
Match(expr *memo.ExprIter) bool
OnTransform(old *memo.ExprIter) (newExprs []*memo.GroupExpr, eraseOld bool, eraseAll bool, err error)
}
PushSelDownAggregation为例,具体介绍上面三个方法的使用方式。
Selection -> Aggregation,作用则是将这个 Selection 下推到 Aggregation 下面,例如 SQL:
select a, sum(b) from t group by a having a > 10 and max(c) > 10中,having 条件里的
a > 10可以下推到 Aggregation 的下方。更具体地来说,只要 Selection 当中的一个 Expression 里的所有列都出现在 group by 的分组列时,我们就可以把这个 Expression 进行下推。
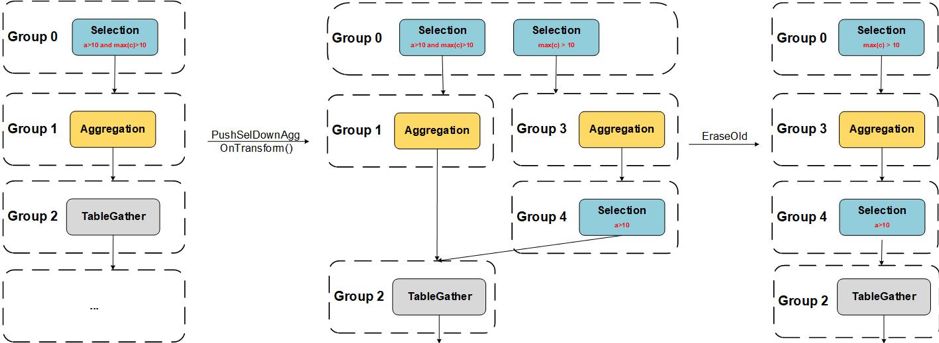
Selection -> Aggregation。
OnTransform()的转换,Selection 中的
a > 10条件被下推到了新的 Aggregation 下方,并且保留的条件
max(c) > 10成为了一个新的 Selection。
OnTransform()的
eraseOld返回了
True,因此最终把原来的 GroupExpr 从 Group 中删除。
Implementation/Implementation Rule
type Implementation interface {
CalcCost(outCount float64, children ...Implementation) float64
SetCost(cost float64)
GetCost() float64
GetPlan() plannercore.PhysicalPlan
AttachChildren(children ...Implementation) Implementation
ScaleCostLimit(costLimit float64) float64
}
ImplementationRule是一个接口类型,用来定义一个逻辑算子的一种物理实现方式。
ImplementationRule
只能通过 Operand 来匹配,因此也需要一个Match()
方法来对算子内部的细节做更细粒度的匹配。OnImplement()
方法用于为 GroupExpr 生成对应的 Implementation。
type ImplementationRule interface {
Match(expr *memo.GroupExpr, prop *property.PhysicalProperty) (matched bool)
OnImplement(expr *memo.GroupExpr, reqProp *property.PhysicalProperty) (memo.Implementation, error)
}
Match()方法中,如果上层节点传递下来的 Prop 非空的话,我们这里就不能够将 Aggregation 转换成 HashAgg;而在
OnImplement()方法中,我们只需要将 LogicalAggregation 转换成 PhysicalHashAgg 就可以了。
type Enforcer interface {
NewProperty(prop *property.PhysicalProperty) (newProp *property.PhysicalProperty)
OnEnforce(reqProp *property.PhysicalProperty, child memo.Implementation) (impl memo.Implementation)
GetEnforceCost(g *memo.Group) float64
}
type LogicalProperty struct {
Stats *StatsInfo
Schema *expression.Schema
}
PhysicalProperty
TiKVTableGather、
TiFlashTableGather甚至
MySQLGather等,这些 Gather 算子最终在物理优化阶段会被改写成
TableReader、
IndexReader等用来读取数据的算子,因此 Gather 的所有父亲算子都是在 TiDB 中执行的,而 Gather 所有子节点的算子都是在相应的存储引擎上执行的。这样做有两个好处:
我们可以在逻辑优化阶段就区分出不同的存储引擎,可以针对不同的存储引擎设计不同的算子下推策略。 若 TiDB 想要使用别的存储引擎,在优化器中只需要实现对应的 Gather 算子以及物理优化阶段的 Reader 算子。
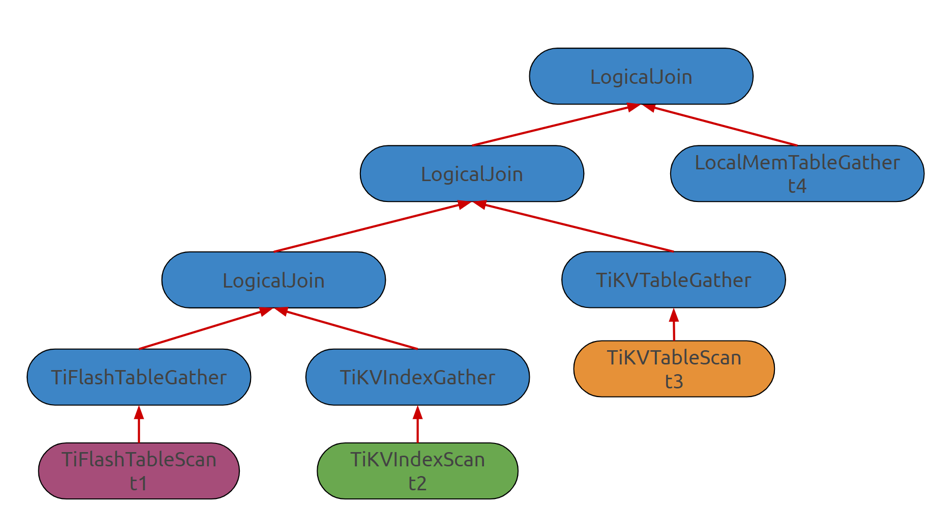
优化过程
Preprocessing phase,预处理阶段。 Exploration phase,逻辑搜索阶段。 Implementation phase,物理实现阶段。
findMoreEquiv(group, groupExpr)是对一个 GroupExpr 应用所有的 Transformation 来搜索更多的逻辑等价的 GroupExpr,其过程如下:
Match()方法进一步判断是否能够匹配相应的细节内容(例如 Join 的类型)。
Match()成功,则调用
OnTransformation()方法来应用相应的变换规则。
OnTransformation返回了新的
GroupExpr,则将这个 GroupExpr 插入到 Group 中,并且将 Group 标记为 UnExplored,保证新生成的 GroupExpr 未来也可以被搜索到。
OnTransformation返回的
eraseOld为
True,那么在
findMoreEquiv()结束后,会将当前的 GroupExpr 从 Group 中删除。
OnTransformation返回的
eraseAll为
True,那么可以删除当前 Group 中的所有 GroupExpr,插入新的 GroupExpr 并结束当前 Group 的搜索。
exploreGroup()方法自底向上递归地对整个 Group Tree 中的 GroupExpr 调用
findMoreEquiv(),主要过程如下:
exploreGroup(),直至子 Group 中不再产生新的 GroupExpr 为止。
findMoreEquiv(),若返回的
eraseCur为
True,则将这个 GroupExpr 从 Group 中删除。
exploreGroup(),直至所有的 Group 都不再产生新的 GroupExpr 为止。
implGroupExpr为一个 GroupExpr 根据上层传递下来的 PhysicalProperty 来生成 Implementation。过程十分简单,就是尝试对当前的 GroupExpr 应用所有对应的 ImplementationRule,最后将匹配成功后产生的 Implementations 返回。
func (opt *Optimizer) implGroupExpr(groupExpr *memo.GroupExpr, reqPhysProp *property.PhysicalProperty) (impls []memo.Implementation, err error) {
for _, rule := range opt.GetImplementationRules(groupExpr.ExprNode) {
if !rule.Match(groupExpr, reqPhysProp) {
continue
}
impl, err := rule.OnImplement(groupExpr, reqPhysProp)
if err != nil {
return nil, err
}
if impl != nil {
impls = append(impls, impl)
}
}
return impls, nil
}
implGroup()根据上层传递下来的 PhysicalProperty 递归地为 Group 生成最优的 Implementation。
Implementation Phase 实际上是一个记忆化搜索的过程,每个 Group 搜索到一个 PhysicalProperty 对应最优的 Implementation 后都会将其记录下来,因此在搜索之前可以先查看是否可以从历史结果中查询到 reqPhysicalProp
对应的最优 Implementation。CostLimit 是在搜索过程中用于预剪枝的 Cost 上界,要注意的是使用 CostLimit 的前提是:Cost 必须自底向上单调递增。我们以下图为例,Expr0 和 Expr1 是 Group0 中逻辑等价的 GroupExpr,Expr0 产生的最优的 Implementation 的 Cost 是 1000,此时我们会用 CostLimit = 1000 去搜索 Expr1,我们的目的是让 Expr1 产生更好的(Cost 更小的)Implementation,但是 Expr1 在向下搜索的过程中,Expr4 的最优 Implementation 的 Cost 是 1200,大于了 CostLimit,也就是说 Expr1 产生的 Implementation 的 Cost 一定是大于 1200 的,所以 Expr1 在这条路径上无论如何都不会比 Expr0 产生的 Implementation 更优,因此我们会将这条搜索路径剪枝,不对 Expr1、Expr3 再进行搜索。
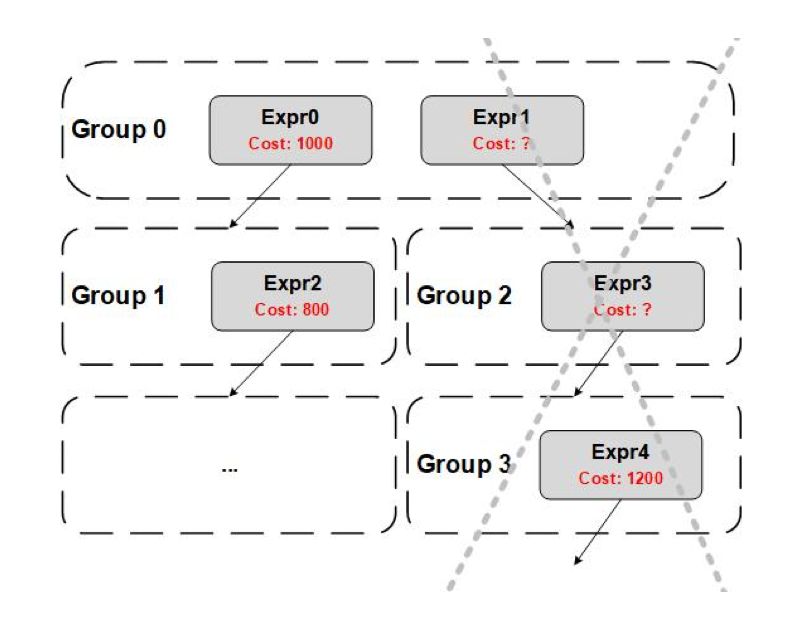
在生成 Implementation 之前会先对当前的 Group 调用 fillGroupStats()
来填充LogicalProperty 里的统计信息。最后就是调用 implGroupExpr()
来产生 Implementation 和递归调用implGroup()
来搜索子 Group 的过程。
select b, sum(c) over (partition by b) from t
b列为分组,由于目前 Window 的实现是需要下层算子根据分组列有序,当没有可以使
b列有序的索引时,我们必须在 Window 算子下面强制添加一个 Sort 算子来满足 Window 算子向下传递的 PhysicalProperty。
总结
💡 文中划线部分均有跳转,点击【阅读原文】查看原版







