numpy“手撕”文本主题模型之LSA

from sklearn.datasets import fetch_20newsgroups 
categories = ['alt.atheism', 'talk.religion.misc', 'comp.graphics', 'sci.space'] 
remove = ('headers', 'footers', 'quotes') 
newsgroups_train = fetch_20newsgroups(subset='train', categories=categories, remove=remove) 
newsgroups_test = fetch_20newsgroups(subset='test', categories=categories, remove=remove)

newsgroups_train.data[:2]
'''
 [
 "Hi,\n\n
  I've noticed that if you only save a model (with all your mapping planes\n
  positioned carefully) to a .3DS file that when you reload it after restarting\n
  3DS, they are given a default position and orientation. But if you save\n
  to a .PRJ file their positions/orientation are preserved. Does anyone\n
  know why this information is not stored in the .3DS file? Nothing is\n
  explicitly said in the manual about saving texture rules in the .PRJ file. \n
  I'd like to be able to read the texture rule information, does anyone have \n
  the format for the .PRJ file?\n\n
  Is the .CEL file format available from somewhere?\n\n
  Rych", 
 '\n\n
  Seems to be, barring evidence to the contrary, that Koresh was simply\n
  another deranged fanatic who thought it neccessary to take a whole bunch of\n
  folks with him, children and all, to satisfy his delusional mania. Jim\n
  Jones, circa 1993.\n\n\n
  Nope - fruitcakes like Koresh have been demonstrating such evil corruption\n
  for centuries.'] 
'''

import numpy as np 
from sklearn.feature_extraction.text import CountVectorizer 
vectorizer = CountVectorizer(stop_words='english') 
vectors = vectorizer.fit_transform(newsgroups_train.data).todense() 
vocab = np.array(vectorizer.get_feature_names())

vectors.shape 
''' 
(2034, 26576) 
'''

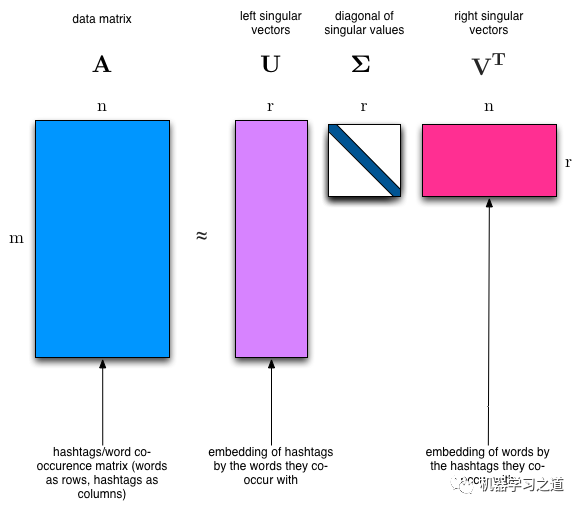
import scipy 
U, s, Vh = scipy.linalg.svd(vectors, full_matrices=False)

# 注意将s从一维向量转换成对角矩阵(diagonal matrix)
np.allclose(U.dot(np.diag(s)).dot(Vh), vectors)  # True
np.allclose(U.T.dot(U), np.eye(U.shape[0]))   # True
np.allclose(Vh.dot(Vh.T), np.eye(Vh.shape[0]))  # True

num_top_words = 8 
def show_topics(a): 
  top_words = lambda t: [vocab[i] for i in np.argsort(t)[:-num_top_words-1:-1]] 
  topic_words = ([top_words(t) for t in a]) 
  return [' '.join(t) for t in topic_words] 
show_topics(Vh[:10]) 


''' 
['ditto critus propagandist surname galacticentric kindergarten surreal imaginative', 
 'jpeg gif file color quality image jfif format', 
 'graphics edu pub mail 128 3d ray ftp', 
 'jesus god matthew people atheists atheism does graphics', 
 'image data processing analysis software available tools display', 
 'god atheists atheism religious believe religion argument true', 
 'space nasa lunar mars probe moon missions probes', 
 'image probe surface lunar mars probes moon orbit', 
 'argument fallacy conclusion example true ad argumentum premises', 
 'space larson image theory universe physical nasa material'] 
'''

from sklearn import decomposition 
u, s, v = decomposition.randomized_svd(vectors, 10)

import fbpca 
u, s, v = fbpca.pca(vectors, 10)