

“社区”一词今年已进入全球主流,这在很大程度上要归因于当前的新型冠状病毒。鉴于对图形和图形理论的一般经验和兴趣,我想了解和探索如何在“社区”中利用这一点,这便是社区发现。
虽然目前的大流行的预测以及其他方面超出了本文的范围,但我觉得社区发现是一个有意义的话题,作为图形理论的一个很好的延伸,每个人都应该至少知道一点。

我在本文中的重点是帮助您认识和初步接触社区发现。当然,这也将依赖于对图论的基本理论。我们将详细讨论社区发现,包括Girvan-Newman算法以及如何在Python中实现它。
正如您可能已经猜到的,本文假设您熟悉图论。如果您不熟悉此主题,可以看我们前几期的文章。
什么是社区
对于图,社区可以定义为节点的子集,这些节点彼此紧密相连,并且松散地连接到同一图形中其他社区的节点。
让我用一个例子来分解它。想想社交媒体平台,如微博、Facebook 或 Twitter,我们尝试在其中与其他人建立联系,我们最终与属于不同社交圈的人联系起来。这些社交圈可以是一群亲戚、同学、同事等,这也是社区。
什么是社区发现
检测网络中的社区是网络分析中最重要的任务之一。在大型网络(如在线社交网络)中,我们可以拥有数百万个节点和边缘。在此类网络中检测社区已成为一项艰巨的任务。因此,我们需要社区发现算法,将网络划分为多个社区。
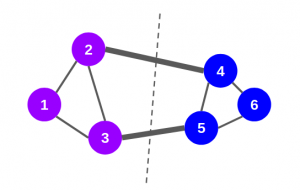
上图为一个图网络结构,由图可以清楚地看出其可以分为两个社区,主要有两种类型的方法来检测图表中的社区:
(a) Agglomerative Methods(凝聚方法)
在凝聚方法中,我们从一个空图开始,该空图由原图的节点组成,但没有边。接下来,将边一个接一个地添加到图中,从“更强”到“更弱”的边开始。这种边缘的强度,或者说边缘的重量,可以用不同的方法计算。
(b) Divisive Methods (分裂方法)
在分裂方法中,我们走的是相反的道路。我们从完全图开始,迭代去掉边。最高重量的边缘首先被去除。在每一步,边权重的计算是重复的,因为剩余的边权重变化后,边被删除。经过一定数量的步骤之后,我们得到密集连接的节点群。
接下来,我们将介绍一种用于社区发现的算法Girvan-Newman 算法——分裂方法的一个例子。
Girvan-Newman 算法
Girvan-Newman 算法的主要思想为,根据中心值之间的边缘,通过迭代删除图形的边缘来发现图形中的社区。首先删除具有最高边缘之间的边缘。我们将在本文的稍后部分介绍此算法,但首先,让我们了解"边缘之间的中心性"的概念。
边缘之间的中心性(EBC) 可以定义为通过网络中边缘的最短路径数。根据图形中所有节点之间的最短路径,每个边线都会获得 EBC 值。
对于图形和网络,最短路径是指覆盖距离最少的任何两个节点之间的路径。让我们以一个示例来更好地学习和理解 EBC 值的计算方式,示例网络结构如下图:
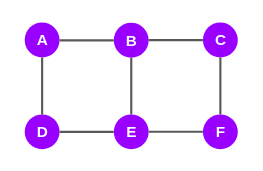
它有 6 个节点和 7 条边,对吗?现在,我们将尝试查找此图中所有边缘的 EBC 值。请注意,这是一个迭代过程,我在这里提供了一个大纲:
1. 我们将一次使用一个节点,并绘制从所选节点到其他节点的最短路径
2. 基于最短路径,我们将计算所有边的 EBC 分数
3. 我们需要对图形中的每个节点重复此过程。
4. 这意味着每条边将得到 6 分,这些分数将添加边缘
5. 最后,每个边的总分将除以 2 以获得 EBC 分数
现在,让我们从节点 A 开始。直接连接到节点 A 的节点是节点 B 和 D。因此,从 A 到 B 和 D 的最短路径分别是 AB 和 AD:
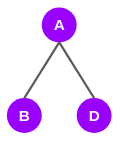
事实证明,从 A 到节点 C 和 E 的最短路径通过 B 和 D:

从节点 A 到最后一个节点 F 的最短路径,通过节点 B、D、C 和 E:
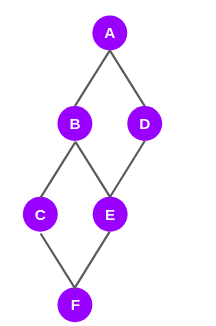
上图仅描述从节点 A 到所有其他节点的最短路径。现在,我们将看到如何给边设定分数。
在给边点分数之前,我们将在最短路径图中为节点分配分数。要分配这些分数,我们必须从根节点(即节点 A)遍历图形到最后一个节点(节点 F)。

如上图所示,节点 B 和 D 各得分为 1。这是因为从节点 A 到其中任一节点的最短路径只有一个。出于同样的原因,节点 C 的分数为 1,因为从节点 A 到节点 C 只有一条最短路径。移动到节点 E。它通过两条最短路径 ABE 和 ADE 连接到节点 A。因此,它得到分数为2。最后一个节点 F 通过三条最短路径连接到ABCF、ABEF 和 ADEF。因此,它得到3分。
为每个节点分配完分数后,接下来,我们将继续计算边的分数。在这里,我们将向后移动,从节点 F 移动到节点 A:
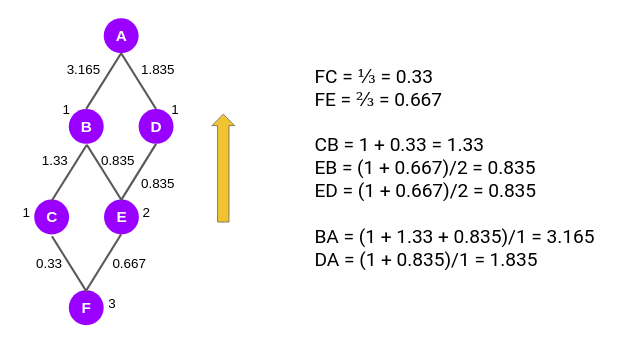
我们首先计算边 FC 和 FE 的分数,正如上图右侧所计算的那样,边 FC 的边缘分数是 C 和 F 的节点分数比率,即 1/3 或 0.33。同样,对于 FE,边缘分数为 2/3。
那么计算边缘 CB、EB 和 ED 的边得分应该怎么计算呢?根据 Girvan-Newman 算法,从该级别开始,每个节点的默认值为 1,上一步中计算的边分数将添加到此值中。
因此,CB的边缘分数为 (1 +0.33)/1。同样,边缘得分EB或ED是(1 + 0.667)/2。同理,我们可以计算得出AB和AD的值。然后对其他五个节点重复相同的步骤,所以网络中的所有边获得了6个不同的分数值,将这6个分数值相加分配给原始图中的边,如下所示:

由于它是一个无向图,我们将这些分数除以2,最后,我们将获得EBC分数:
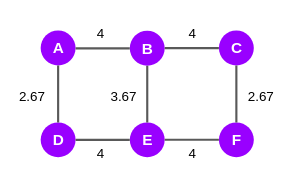
根据 Girvan-Newman 算法,计算 EBC 分数后,最高分的边将被拆分,直到图形拆分为两个点。因此,在上图中,我们可以看到边缘 AB、BC、DE 和 EF 得分最高。我们将删除这些边,得到了 3个子图, 我们可以称之为社区:
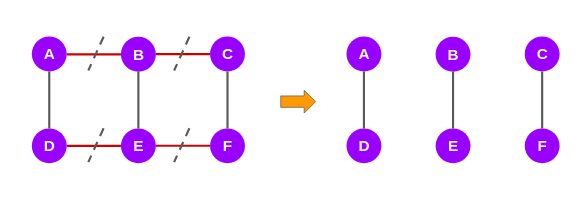
怎么样是不是通过实例,对 Girvan-Newman 算法和社区理解地更深入了些呢?下面让我们一起来看看如何用python去实现Girvan-Newman 算法。
Girvan-Newman算法的python实现
我们将使用Zachary的空手道俱乐部图来演示如何使用Girvan Newman算法实现社区发现。扎卡里的空手道俱乐部是一个大学空手道俱乐部的社交网络,在2002年被Michelle Girvan和Mark Newman使用后,该网络成为网络中社区结构的一个流行示例。
我们将从加载所需的库开始:networkx和matplotlib:
import networkx as nx
import matplotlib.pyplot as plt
空手道俱乐部图是预先安装在networkx库中的。所以,我们可以很容易地导入它
# load the graph
G = nx.karate_club_graph()
# visualize the graph
nx.draw(G, with_labels = True)
我们可以得到空手道俱乐部图结构如下所示,可以看出,该图有34个节点和78条边,这是一个相当小的图形。通常,现实世界中的图形很容易比这个图形大一千倍。
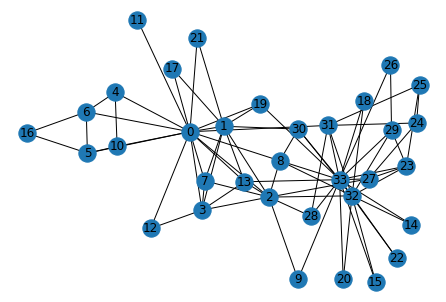
现在,我们知道在Girvan-Newman方法中,图的边是根据EBC分数逐个消除的。所以,第一个任务是找到所有边的EBC值,然后取最大值的边。以下函数执行删除网络结构中边的操作:
def edge_to_remove(graph):
G_dict = nx.edge_betweenness_centrality(graph)
edge = ()
# extract the edge with highest edge betweenness centrality score
for key, value in sorted(G_dict.items(), key=lambda item: item[1], reverse = True):
edge = key
break
return edge
下面的函数将使用上面的函数将图划分为多个社区:
def girvan_newman(graph):
# find number of connected components
sg = nx.connected_components(graph)
sg_count = nx.number_connected_components(graph)
while(sg_count == 1):
graph.remove_edge(edge_to_remove(graph)[0],
edge_to_remove(graph)[1])
sg = nx.connected_components(graph)
sg_count = nx.number_connected_components(graph)
return sg
接下来,让我们将空手道俱乐部图传递给上面的函数
# find communities in the graph
c = girvan_newman(G.copy())
# find the nodes forming the communities
node_groups = []
for i in c:
node_groups.append(list(i))
通过输出结果 node_groups
Output: [[0, 1, 3, 4, 5, 6, 7, 10, 11, 12, 13, 16, 17, 19, 21],
[32, 33, 2, 8, 9, 14, 15, 18, 20, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31]]
根据Girvan-Newman算法,这些是属于空手道俱乐部图中两个社区的节点集。我们可以使用这些节点集来可视化图中发现的社区:
# plot the communities
color_map = []
for node in G:
if node in node_groups[0]:
color_map.append('blue')
else:
color_map.append('green')
nx.draw(G, node_color=color_map, with_labels=True)
plt.show()

上图便是通过上述一系列算法执行得到的两个社区的可视化结果。
至此,本文介绍的知识就结束啦~在本文中,我们讨论了图论的一个最重要的应用-社区发现,详细介绍了GirvaniNewman算法,它是一种常用的用于社区发现的图划分算法,最后我们用python实现了该算法。其实呢,还有很多其他的算法来实现社区发现,有机会后面再一起分享。

本文作者:


指导老师:


长按二维码关注我们吧~

长按二维码关注沈浩老师公众号~
原文链接:
https://www.analyticsvidhya.com/blog/2020/04/community-detection-graphs-networks/






