图论|第二期： 关于复杂网络中的关键节点

又见面啦！在上一篇关于图论的公众号中，我们介绍了图论的入门知识，包括图论的起源——著名的“七座小桥”问题，以及如何利用Networkx去生成一个网络拓扑结构并可视化。

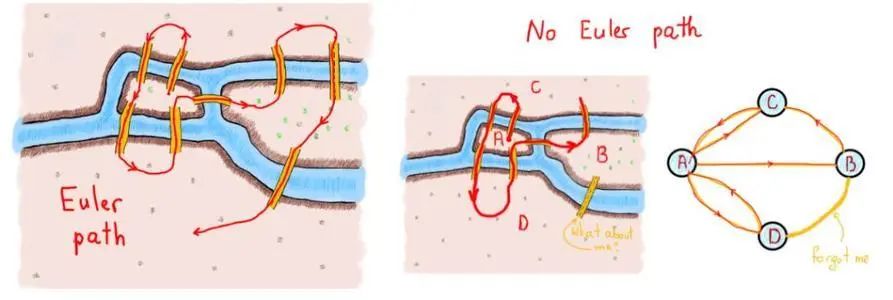
你是不是还有印象呢？

什么？

不记得了。

没关系，传送门在下面

在上次图论介绍的基础上，今天想跟大家聊一聊复杂网络结构中关键节点的那些事。

复杂网络中被提及最多的两个模型当属“小世界网络”模型和“无标度网络”模型。小世界网络模型表示的是在网络中，一个节点到网络中任意节点的路径都不会太长，中间经过的中间节点数量并不大，就仿佛这个网络是一个小世界。而无标度网络模型是带有一类特性的复杂网络。其典型特征是在网络中的大部分节点只和很少节点连接，而有极少的节点与非常多的节点连接。这种关键节点（称为“枢纽”或“集散节点”）的存在使得无尺度网络对意外故障有强大的承受能力，但面对协同性攻击时则显得脆弱。

你是不是想问，这种关键节点的重要性在具体生活中体现在哪里呢？

·维持互联网连通性的Hub节点

·引起大规模级联失效的发电站

·触发生物链连锁反应的海獭

·引爆信息的超级传播者

·导致全球经济危机的美国次贷危机

本篇文章想要介绍的问题就是，如何去衡量一个复杂网络结构中节点的重要性呢？

还记得吗？在上一期推送中我们创建出了一个复杂的网络结构模型，下面我们将介绍几个衡量节点重要性的指标，并在该网络结构上进行计算和介绍，跟着我们一起来学习认识一下吧！

度中心性衡量的是连接到节点的边的个数，通过度中心性的大小我们可以获得连接节点数最多的节点。在有向图中，度中心性分为输入边缘的入度和输出边缘的出度。在计算时，我们只需要将连接到该节点的边的数量相加，然后除以节点总数减一即可。其数学公式如下：

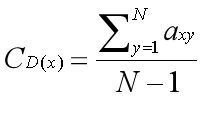
其中N是图结构中的节点数，a取值为0或1（节点x与节点y之间有连接取1；反之取0）。基于Networkx可以用以下代码计算每个节点的度中心性的值。

for node in G.nodes():
         print(node, nx.degree_centrality(G)[node])

下面我们在所创建出的图结构中进行度中心性的计算，所得结果如下：

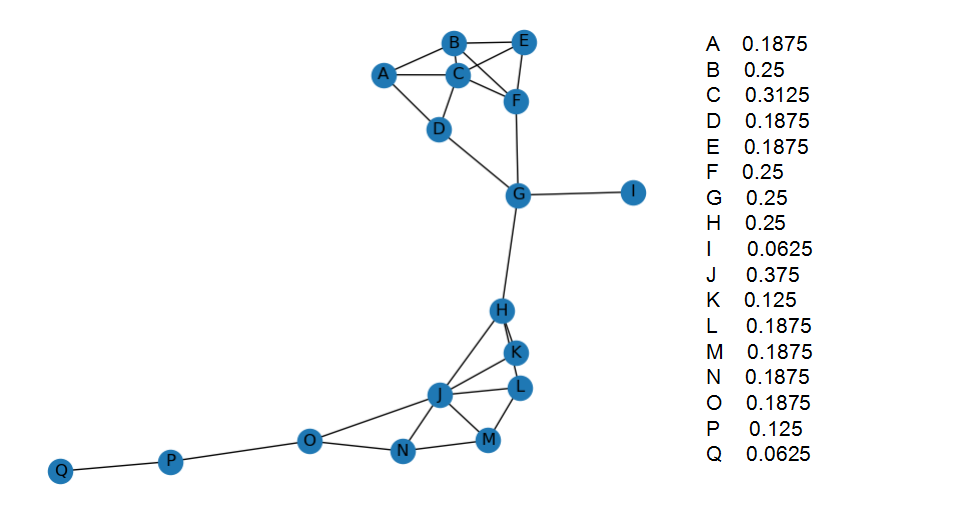
图左侧为网络结构图 右侧为其度中心性计算结果

从数据结果可以很清晰地看出，节点J具有最大的中心度。在图中我们也可以很容易地看出节点J连接的边数最大。

怎么样，是不是觉得度中心性很好理解呢？那我们一起继续学习吧~

接近中心性衡量的是从一个节点到任何其他节点的平均距离。一个节点越中心，它与所有其他节点越近。你可能会疑惑这样的算法和评价标准有什么实际意义呢？设想一下，城市中要建一个大型的娱乐商场，作为投资方的你希望周围社区的顾客到达这个商场的距离都尽可能地短。这就涉及到了接近中心性的问题。节点的接近度通常以其归一化形式表示，其数学表达式如下：

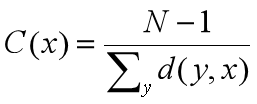
其中N是图上节点的数量，d(y,x)是顶点x和y之间的距离。基于Networkx可以用以下代码计算每个节点的接近中心性的值。

for node in G.nodes():
    print(node, nx.closeness_centrality(G)[node])

下面我们在所创建出的图结构中进行接近中心性的计算，所得结果如下：

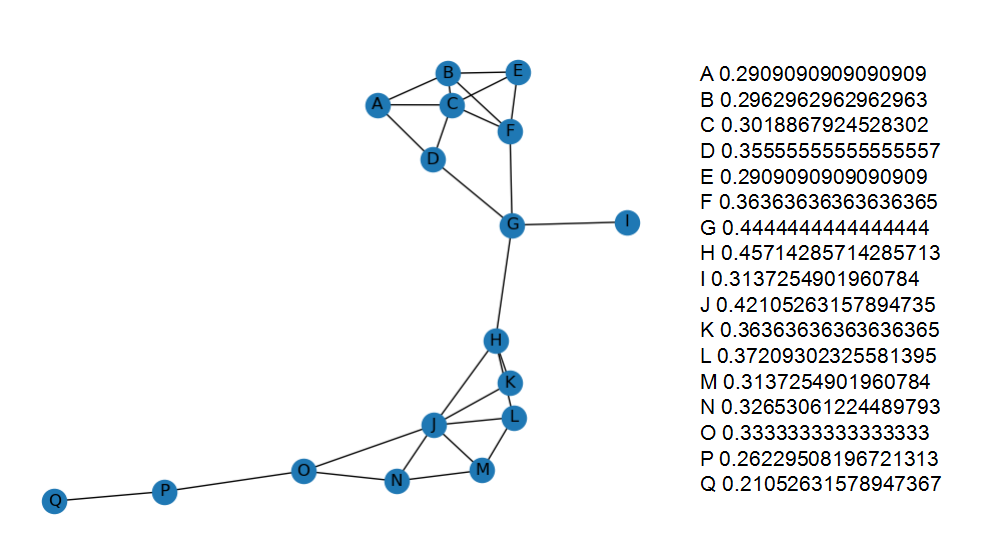
图左侧为网络结构图 右侧为其接近中心性计算结果

由结果可以看出节点H为接近中心性最高的节点，这意味着节点H比其他所有节点都更接近大多数节点。

中间中心性度量节点所在的最短路径的数量，通常用于确定通过图形的信息流。数值越高，表示流经该节点的信息越多。中间中心性指的是一个结点担任其它两个结点之间最短路的桥梁的次数。一个结点充当“中介”的次数越高，它的中介中心度就越大。中间中心性可通过以下公式计算：

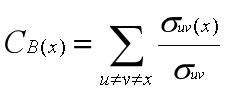
其中分母是顶点u和v之间最短路径的数量，而分子是顶点u和v之间经过顶点x的最短路径的数量。基于Networkx可以用以下代码计算每个节点的中间中心性的值。

for node in G.nodes():
     print(node, nx.betweenness_centrality(G)[node])

下面我们在所创建出的图结构中进行对各节点的中间中心性的计算，所得结果如下：

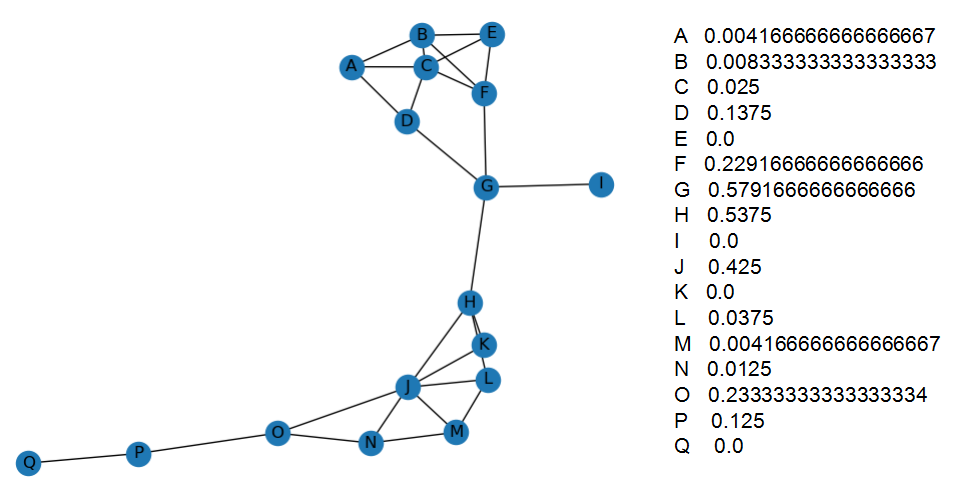
图左侧为网络结构图 右侧为其中间中心性计算结果

由数据可以看出节点G具有最高的中间中心性值，在图中也可以很容易地得到验证，节点G具有最高的居中性。

特征向量中心性的基本思想是，一个节点的重要性取决于其邻居节点，将单个节点的重要性看成是所有其它节点重要性的线性组合，进行迭代计算。换句话说，就是与你连接的人越重要，你就越重要。

特征向量中心性比前三个中心性的原理和计算都复杂一点，在数学上，特征向量中心性由下式计算：

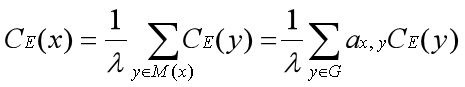
其中λ是计算出的最大特征值，M（x）是顶点x的一组邻居，y是邻近的顶点，G是要评估的图。根据x和y是否是邻居，a取一个值或0或1 。该表达式是特征向量方程的解

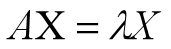
在这种情况下，A是邻接矩阵，它本质上计算矩阵形式的节点之间的连接数，λ是特征值，X是我们要求解的特征向量。在处理大型矩阵时，为了避免找到其特征值解，我们一般使用迭代过程来找到特征向量。

是不是还是觉得迷迷糊糊找不到关键呢？

别怕，看不懂的不止你一个。

下面有一个具体的例子~

我们给定一个简单的图结构，如下图所示：

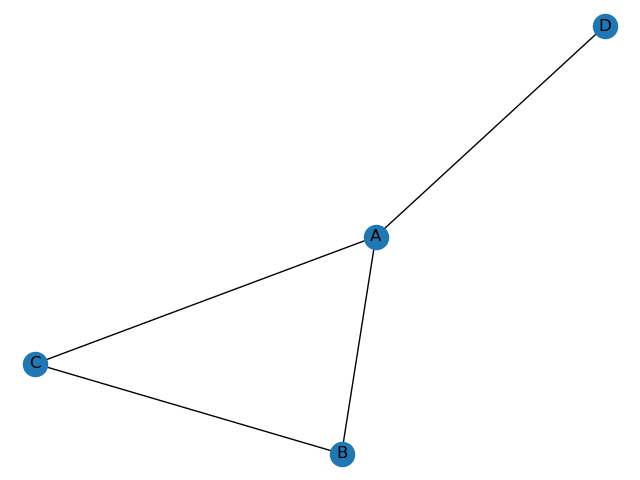
根据图的结构，我们就容易能得到其对应的邻接矩阵，如下图：

从这里开始，我们将此矩阵乘以我们的初始向量，该向量只是1的向量。我们得到如下的计算过程：

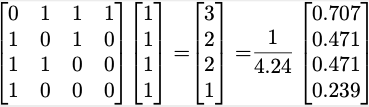
从这里开始，我们将归一化的向量替换为初始向量，然后将其重新插入方程式。重复此过程如下：

这个过程一直持续到特征向量收敛到稳定解为止。在此示例的情况下，最终结果是

现在我们大概了解了如何计算特征向量中心性，下面我们基于Networkx在所创建出的图结构中进行对各节点的特征向量中心性的计算。代码如下：

for node in G.nodes():
    print(node,nx.eigenvector_centrality(G,max_iter=1000)[node])

所得结果如下：

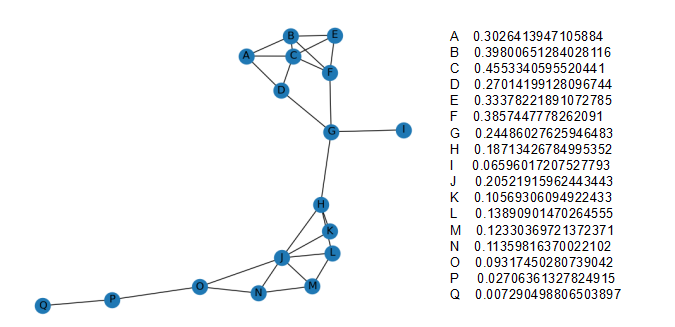
图左侧为网络结构图 右侧为其特征向量中心性计算结果

这表明节点C具有最大的特征向量中心性。

关于图论和中心性的测量要介绍的东西还有许多，这些都只是茫茫大海中的几粒砂砾。今天介绍的几种衡量节点关键型的度量指标你都学会了吗？那我们下期见~带你继续领略图论的风采！

长按二维码关注我们吧~

长按二维码关注沈浩老师公众号~

原文链接：