今天是我坚持写题解的第 57 天！

题目描述（Medium）

给你 二维 平面上两个 由直线构成的 矩形，请你计算并返回两个矩形覆盖的总面积。

每个矩形由其 左下 顶点和 右上 顶点坐标表示：

• 
  

• 第一个矩形由其左下顶点 (ax1, ay1)
  和右上顶点 (ax2, ay2)
  定义。

• 
  

• 第二个矩形由其左下顶点 (bx1, by1)
  和右上顶点 (bx2, by2)
  定义。

示例 1：

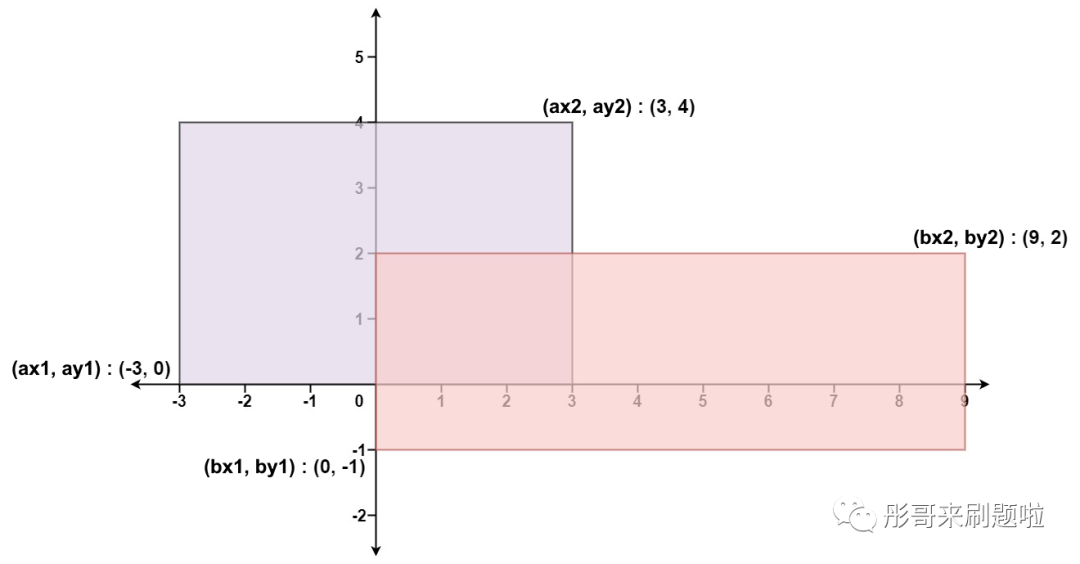
输入：ax1 = -3, ay1 = 0, ax2 = 3, ay2 = 4, bx1 = 0, by1 = -1, bx2 = 9, by2 = 2
输出：45

示例 2：

输入：ax1 = -2, ay1 = -2, ax2 = 2, ay2 = 2, bx1 = -2, by1 = -2, bx2 = 2, by2 = 2
输出：16

提示：

• -104 <= ax1, ay1, ax2, ay2, bx1, by1, bx2, by2 <= 104
  

方法、模拟

今天这道题大家一看都会：结果等于两个矩形的面积相加减去相交部分的面积，关键在于如何求解相交部分的面积。

我们先考虑两个矩形在 x
坐标的相对位置情况，一共有以下 6 种：

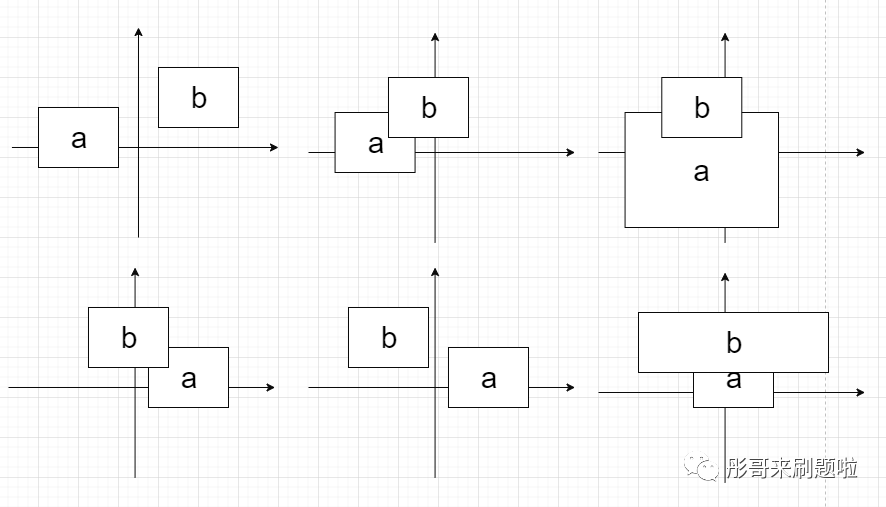
可以看到，只要两者相交，在 x
坐标上相交部分右边的坐标肯定是两者右边 x
坐标中的较小者，左边的坐标肯定是两者左边 x
坐标中的较大者，所以，我们拿 min(ax2,bx2) - max(ax1, bx1)
就可以得出相交矩形的宽度，但是，对于不相交的情况，按这个公式相减你会得到负数，对于这种情况，我们再把它跟 0
比较取较大者即可：max(0, min(ax2,bx2) - max(ax1, bx1))
。

同理，在 y
坐标上求相交部分的高度公式可以很轻易地得出为：max(0, min(ay2,by2) - max(ay1,by1))
。

相交部分的宽度和高度都计算出来了，再计算面积就简单了。

请看代码：

class Solution {
    public int computeArea(int ax1, int ay1, int ax2, int ay2, int bx1, int by1, int bx2, int by2) {
        int shadowWidth = Math.max(0, Math.min(ax2, bx2) - Math.max(ax1, bx1));
        int shadowHeight = Math.max(0, Math.min(ay2, by2) - Math.max(ay1, by1));
        return area(ax1, ay1, ax2, ay2) + area(bx1, by1, bx2, by2) - area(shadowWidth, shadowHeight);
    }

    private int area(int x1, int y1, int x2, int y2) {
        return area(x2 - x1, y2 - y1);
    }

    private int area(int width, int height) {
        return width * height;
    }
}

• 时间复杂度：。
• 空间复杂度：。

运行结果如下：

最后

如果对你有帮助，请点个赞吧，谢谢^^

也可以关注我，每日分享题解，一起刷题，一起拿全家桶。