今天是我坚持写题解的第 35 天!

题目描述(Hard)
假设 力扣(LeetCode)即将开始 IPO 。为了以更高的价格将股票卖给风险投资公司,力扣 希望在 IPO 之前开展一些项目以增加其资本。 由于资源有限,它只能在 IPO 之前完成最多 k 个不同的项目。帮助 力扣 设计完成最多 k
个不同项目后得到最大总资本的方式。
给你 n
个项目。对于每个项目 i
,它都有一个纯利润 profits[i]
,和启动该项目需要的最小资本 capital[i]
。
最初,你的资本为 w
。当你完成一个项目时,你将获得纯利润,且利润将被添加到你的总资本中。
总而言之,从给定项目中选择 最多 k
个不同项目的列表,以 最大化最终资本 ,并输出最终可获得的最多资本。
答案保证在 32
位有符号整数范围内。
示例 1:
输入:k = 2, w = 0, profits = [1,2,3], capital = [0,1,1]
输出:4
解释:由于你的初始资本为 0,你仅可以从 0 号项目开始。
在完成后,你将获得 1 的利润,你的总资本将变为 1。
此时你可以选择开始 1 号或 2 号项目。
由于你最多可以选择两个项目,所以你需要完成 2 号项目以获得最大的资本。
因此,输出最后最大化的资本,为 0 + 1 + 3 = 4。
示例 2:
输入:k = 3, w = 0, profits = [1,2,3], capital = [0,1,2]
输出:6
提示:
1 <= k <= 105
0 <= w <= 109
n == profits.length
n == capital.length
1 <= n <= 105
0 <= profits[i] <= 104
0 <= capital[i] <= 109
链接:https://leetcode-cn.com/problems/ipo
题目理解
我们先搞清楚题目在说啥,简单用一句话总结:初始时你手里的钱是 w
,要拿这笔钱从 n
个项目中投资 k
个项目,保证最后你手里的钱最多,每个项目有利润 profits
和成本 capital
。
我们做两种假设:
假设一:假如你手里的钱有很多,超过了每个项目的成本。 假设二:你手里的钱有限,只能投资有限的几个项目。
对于假设一,因为我手里的钱超过了每个项目的成本,所以,我是不是每次投资利润最大的项目就可以了?是的,没错。因此,针对这种情况,我们直接取前 k
大利润的项目返回即可。
对于假设二,因为我手头有点紧张,所以,我每次都要谨慎选择,我每次都选择在我能力范围内能获得最大利润的项目,才能使得最后我手里的钱最多,对不对?这就是贪心的思想。
好了,理解了题目的意思,写起代码来就简单了。
方法一、暴力
对于上面的分析,我们可以先把代码的架子搭起来:
class Solution {
public int findMaximizedCapital(int k, int w, int[] profits, int[] capital) {
// 规范化一下 k,使其小于等于 n
k = Math.min(k, profits.length);
// 检测是否可以加速
boolean canSpeedUp = canSpeedUp(w, capital);
if (canSpeedUp) {
// 可以加速,直接按利润排序取前 k 大的就可以了
return speedUp(k, w, profits);
}
// 不能加速,每次取能力范围内的最大利润,取 k 轮
return normal(k, w, profits, capital);
}
}
这其实是一种自顶向下的编码方式,这样架子搭起来之后,我们只要补充每一个方法内部的代码就可以了。
我们先来看第一个方法 canSpeedUp()
,这个方法就是检测是假设一还是假设二的,检测的方法也很简单,就是看是不是每个项目的成本都小于我现在拥有的钱:
private boolean canSpeedUp(int w, int[] capital) {
for (int i = 0; i < capital.length; i++) {
// 如果拥有的资本不能投资所有项目,说明不能加速
if (w < capital[i]) {
return false;
}
}
return true;
}
再来看第二个方法 sppedUp()
,对于假设一,我们直接取前 k
大利润的项目即可,所以,它跟成本 capital
都没啥关系了,直接把 profits
排个序取前 k
大即可:
private int speedUp(int k, int w, int[] profits) {
// 取前 k 大的利润
Arrays.sort(profits);
for (int i = profits.length - 1; i >= profits.length - k; i--) {
w += profits[i];
}
return w;
}
最后来看第三个方法 normal()
,对于假设二,我们每轮都要在现有的能力范围内取最大利润的项目,所以,暴力一点,两层循环即可:
private int normal(int k, int w, int[] profits, int[] capital) {
// 共进行 K 轮投资
for (int i = 0; i < k; i++) {
int maxIndex = -1;
int maxProfit = -1;
for (int j = 0; j < profits.length; j++) {
// 每次选能力范围内利润最大的
if (w >= capital[j] && profits[j] > maxProfit) {
maxProfit = profits[j];
maxIndex = j;
}
}
// 如果这一轮没有可投资的项目了,下一轮肯定也没有,直接退出循环
if (maxIndex == -1) {
break;
}
// 拥有的资本加上最大利润
w += maxProfit;
// 将投资过的项目的成本修改为无限大,这样下次就不会再投资了
capital[maxIndex] = Integer.MAX_VALUE;
}
return w;
}
至此,完整的代码写完了,通过这种自顶向下的编码方式,不仅能使你的代码逻辑更清晰,同时也更加具有可维护性,这种思考方式大家一定要掌握。
最后,我们给出完整的代码:
class Solution {
public int findMaximizedCapital(int k, int w, int[] profits, int[] capital) {
// 规范化一下 k,使其小于等于 n
k = Math.min(k, profits.length);
// 检测是否可以加速
boolean canSpeedUp = canSpeedUp(w, capital);
if (canSpeedUp) {
// 可以加速,直接按利润排序取前 k 大的就可以了
return speedUp(k, w, profits);
}
// 不能加速,每次取能力范围内的最大利润,取 k 轮
return normal(k, w, profits, capital);
}
private boolean canSpeedUp(int w, int[] capital) {
for (int i = 0; i < capital.length; i++) {
// 如果拥有的资本不能投资所有项目,说明不能加速
if (w < capital[i]) {
return false;
}
}
return true;
}
private int speedUp(int k, int w, int[] profits) {
// 取前 k 大的利润
Arrays.sort(profits);
for (int i = profits.length - 1; i >= profits.length - k; i--) {
w += profits[i];
}
return w;
}
private int normal(int k, int w, int[] profits, int[] capital) {
// 共进行 K 轮投资
for (int i = 0; i < k; i++) {
int maxIndex = -1;
int maxProfit = -1;
for (int j = 0; j < profits.length; j++) {
// 每次选能力范围内利润最大的
if (w >= capital[j] && profits[j] > maxProfit) {
maxProfit = profits[j];
maxIndex = j;
}
}
// 如果这一轮没有可投资的项目了,下一轮肯定也没有,直接退出循环
if (maxIndex == -1) {
break;
}
// 拥有的资本加上最大利润
w += maxProfit;
// 将投资过的项目的成本修改为无限大,这样下次就不会再投资了
capital[maxIndex] = Integer.MAX_VALUE;
}
return w;
}
}
时间复杂度:,按最坏的情况算需要遍历 轮,每轮需要遍历 次,这里假设 是规范后的 ,否则应写为 。
空间复杂度:,能够加速的情况下排序需要消耗 的额外空间,不能够加速的情况下是 ,我们这里按不能加速的情况更多来考虑,摊还空间复杂度为 。
摊还空间复杂度,可以理解为均摊空间复杂度或者平均空间复杂度。
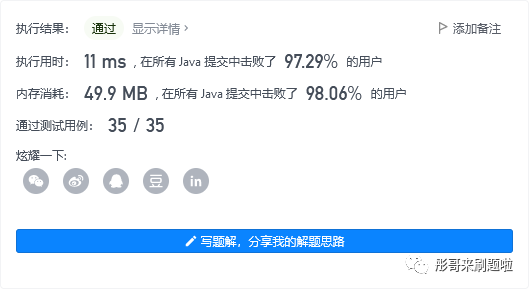
运行结果如下:
方法二、大顶堆
对于假设二,我们也可以使用大顶堆来“优化”,详细的解释都在代码里了,请看代码:
class Solution {
public int findMaximizedCapital(int k, int w, int[] profits, int[] capital) {
// 规范化一下 k,使其小于等于 n
k = Math.min(k, profits.length);
// 检测是否可以加速
boolean canSpeedUp = canSpeedUp(w, capital);
if (canSpeedUp) {
// 可以加速,直接按利润排序取前 k 大的就可以了
return speedUp(k, w, profits);
}
// 不能加速,每次取能力范围内的最大利润,取 k 轮
return normal(k, w, profits, capital);
}
private boolean canSpeedUp(int w, int[] capital) {
for (int i = 0; i < capital.length; i++) {
// 如果拥有的资本不能投资所有项目,说明不能加速
if (w < capital[i]) {
return false;
}
}
return true;
}
private int speedUp(int k, int w, int[] profits) {
// 取前 k 大的利润
Arrays.sort(profits);
for (int i = profits.length - 1; i >= profits.length - k; i--) {
w += profits[i];
}
return w;
}
private int normal(int k, int w, int[] profits, int[] capital) {
int n = profits.length;
// 把成本和利润规范化到一起,方便后面一起排序
int[][] projects = new int[n][2];
for (int i = 0; i < n; i++) {
projects[i][0] = capital[i];
projects[i][1] = profits[i];
}
// 按成本排序,这样后面按成本顺序取即可
Arrays.sort(projects, (a, b) -> a[0] - b[0]);
// 记录取到第几个项目了
int curr = 0;
// 大顶堆,存储能力范围内的项目的利润,堆顶是最大的利润
PriorityQueue<Integer> heap = new PriorityQueue<>((a, b) -> b - a);
// 共进行 k 轮投资
for (int i = 0; i < k; i++) {
// 取当前能力范围内的项目,扔到堆里,堆顶为最大的利润
while (curr < n && projects[curr][0] <= w) {
heap.offer(projects[curr][1]);
curr++;
}
// 没有项目可做了
if (heap.isEmpty()) {
break;
}
// 本轮取出最大利润,然后进入下一轮
w += heap.poll();
}
return w;
}
}
时间复杂度:,排序需要 的时间复杂度,后面取 轮需要 的时间复杂度,因为我们对 进行了规范化,所以,可以保证遍历时的 是小于等于 的,所以,总的时间复杂度为 。 空间复杂度:, 数组及堆需要占用 的额外空间。
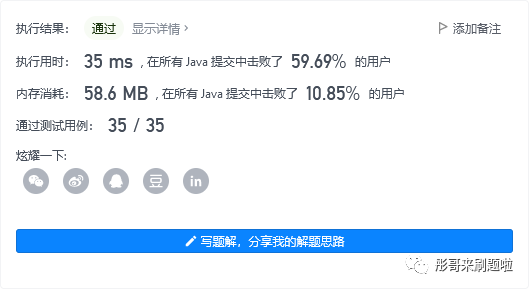
运行结果如下,可以看到,比暴力还慢一些,跟用例的关系很大:
最后
如果对你有帮助,请点个赞吧,谢谢^^
也可以关注我,每日分享题解,一起刷题,一起拿全家桶。






