mass tree

概述

mass tree 是 2012 年提出的，结构上是Trie 和 B+ tree 的结合，其中每一棵 B+ 树以固定长度表示变长的 key 。

mass tree 可以高效地处理任意长度的二进制的 key，包括那些共享前缀的 key 。

mass tree 上的读操作采用乐观并发控制，不需要加锁，也不会将读出的数据放入共享数据结构；写操作只需要锁住当前要更新的节点，允许一个树中多个写操作并行执行。

查询过程中的耗时由树搜索过程中查询的高度决定，为此 mass tree 使用高扇出设计来减少树高；并且会预取 node ，以尽可能减少时延；同时设计了数据的 lay out，尽可能减少缓存中占用的空间。

使用日志及checkpoint技术保证持久性和一致性

虽然上述提到的技术在很多其他地方出现过，但 mass tree 是第一个将这些技术结合在一起的。

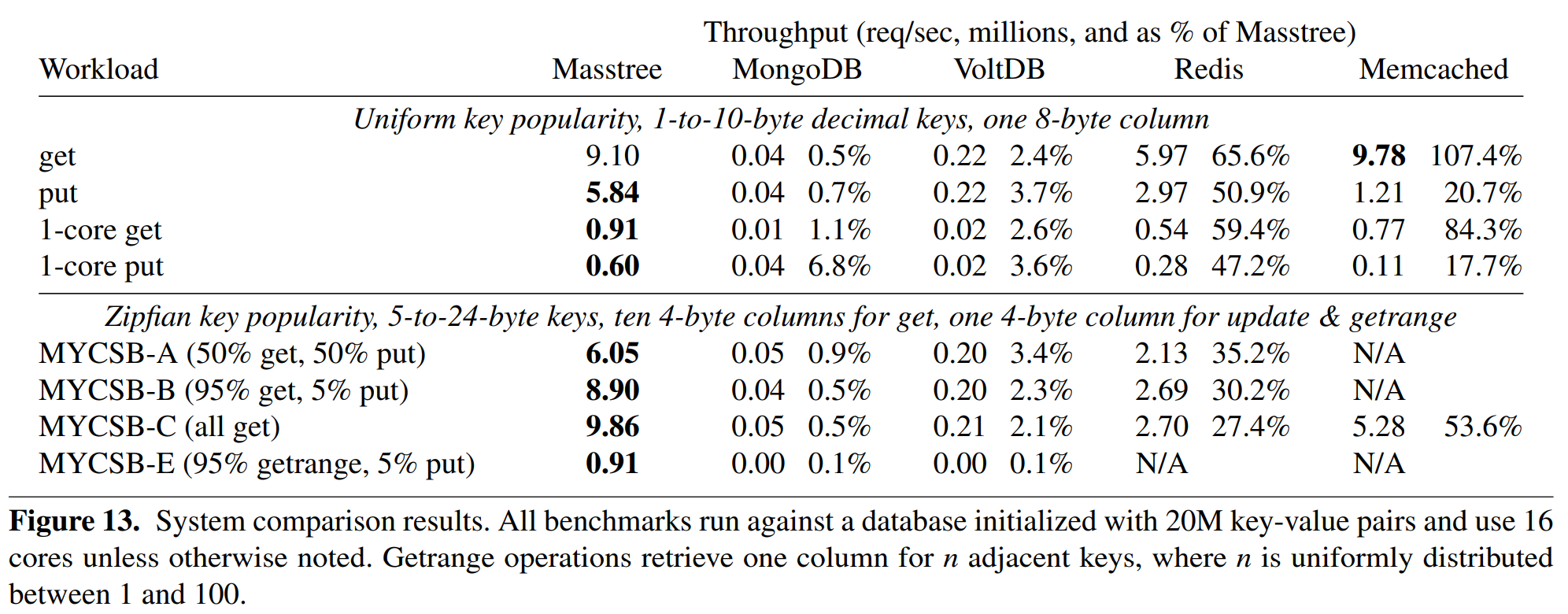
在 16 核的机器上测试，打开日志，查询请求通过网络发送， mass tree 可以达到超过 600w/s 的简单查询。这个数据和memcached、非持久化的 hash-table 服务相当，通常比 VoltDB、MongoDB 和 Redis 高很多。

结构

在结构上 mass tree 可以视作 Trie 和 B+ tree 的结合，Trie 中的一个节点，是一棵 B+ 树。

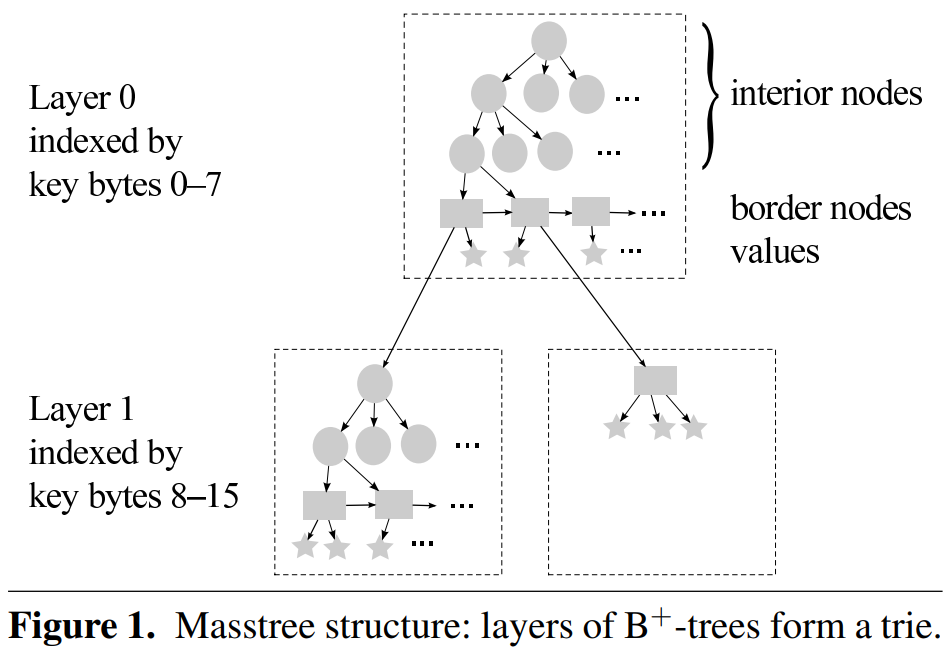
mass tree 的结构如上图所示，圆形的节点称为 interior node，也就是 B+ 树中的非叶子节点，矩形称为 border node，也就是 B+ 树中的叶子节点。五角星代表 value。

mass tree 的 border node 上可能存放的是 value ，也有可能是下一层  B+ 树的根节点。

对于每一层的 B+ 树，用 8 字节表示，长度小于 （8h + 8）的 key 会被放在小于等于 h 的层上，例如 key 的长度是 8，那 key 会出现在第 0 层；再比如到目前为止出现的 key 的长度都是 8 字节，突然来了一个 1KB 的 key，并不会根据长度计算把它放到一百多层。而是看它和当前出现的 key 有没有可以共用的前缀，如果没有就放到 0 层，有的话放到一层。

相关技术

mass tree 是基于许多之前出现过的技术提出的。

例如， 

OLFIT (Optimistic Latch Free Index Access Protocol) 是一种乐观并发控制技术，写操作会更新 node 的 version number，而读操作会在读之前和之后获取 node 的 version number，如果发现 version number 发生了变化 （表明读操作可能获取了不一致的状态），则本次读操作需要重试。mass tree 借鉴了这个技术，但做了一些修改，把 version number 分为两部分，此外还做了其他一些优化旨在减少读操作过程中重试的频率。

缓存命中率是数据库系统中的性能的一个瓶颈点，很多技术被用于改进缓存的命中率，例如预取树的节点，mass tree 也采用了这一技术。

很多 KV 存储相对传统数据库用更好的性能，主要因为其中的查询和数据模型更简单，mass tree 更专注于提升多核下单机的性能，而不是通过数据分区或集群的模式去获得高性能。

...

接口

mass tree 可以作为 KV 存储服务使用，处理读写请求。其中的 value 可与进一步细分为列，每一列都是一个字节串。

mass tree 提供四种接口：

getc(k)

putc(k, v)

removec(k)

getrangec(k, n)

其中 c 是一个可选的参数，用来指定 value 中的部分列。 getrange 方法，也可以称为 scan ，用来按照字母序返回从 k 开始的 n 个 k-v pair。

Masstree

mass tree 中 key 是有序的，用以支持 range 查询。

设计 mass tree 时主要考虑了三个点：
1. mass tree 要高效地支持各种的 key 的类型，包括变长的二进制 key ，其中很多 key 可能共享前缀。

2. 为了获取高性能和高扩展性，mass tree 需要很好地解决并发问题，读操作的数据不能写共享数据结构，以防止 shared cache line 失效。

3. mass tree 必须支持预取，在少量的 cache line 上放入重要的数据。

2，3 两个点构建了 mass  tree 的性能竞争力。

实现上，mass tree 是一个扇出为 2^64 的 Trie，其中每一个节点是一棵 B+ 树。

Trie 的结构能够有效支持有共同前缀的长 key，而  B+ 树结构能有效支持短 key，并且获得较好的并发能力。

在 Trie 和 B+ 树之间选择一个合适的扇出，能够有效地利用 cache line。

换句话说，ｍass tree 包含多层 B+ 树，同一层的 B+ 树共享其上层 B+ 树所表示的前缀。

mass tree 生成新节点是惰性的，如果可以使用现有的部分，不会新生成新节点。

在有 key 被删除时，如果出现完全为空的 tree 会删除，但不会因为删除重新排列 key 。

举例：

1.  t.put("01234567AB") 在 layer 0 存储 key "01234567AB"，其中 key "01234567" 和 2 byte 大小的后缀 "AB" 分开存储。get 时候，先查找 key ，在比较后缀。

2.  t.put("01234567XY") 由于可以和第一条数据共享 8 byte 的前缀， mass tree 建一个新的 layer ，将 "AB" 和 "XY" 放到新 B+ 树的叶子节点上，用新的结构替换原来 layer 0 中 "01234567AB"。对于读操作而言，要么读到原来的 "01234567AB"，要么读到现在的新的结构，无论是哪种，都可以查到"01234567AB" 这条数据。

3. t.remove("01234567XY")，结构并不会变为 "01234567XY" 插入之前的样子，"AB" 仍然保留在 layer 1 中。

mass tree 中节点数据结构如下图所示：

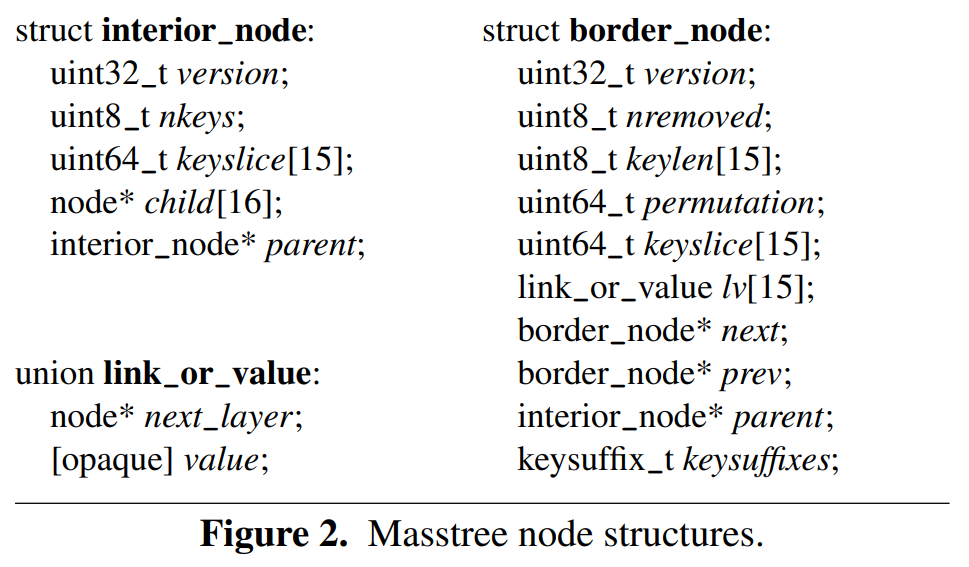
B+ 树每个节点可以放 15 个 key，叶子节点之间通过指针链接起来，用以支持 remove 和 getrange。

keyslice 变量用于存储 8 子节的 key ，必要时字节之间可以交换，以便本地进行比较时能获得与字典序比较相同的结果，这是非常有用的编码技巧，能将性能提升 13%-19% 。对于较短的 key ，用 0 进行填充。

border  node 存储 key slice， length 及 suffix。

其中 length 用于区分有相同 key slice 的 key ，因为要支持二进制的 key 。例如，8-byte 的 key "ABBCDEFG\0" 和 7-byte 的 key "ABCDEFG" 它们 slice 是一样的，但长度不一样。确保具有相同 slice 的 key 存储在相同的 border node 中，这可以简化 interior node 缩小 interior node 的规模，同时简化并发操作相关的一些重要变量的维护，代价是分裂时需要做一些检查。 

suffix 存储在 keysuffixes 中，mass tree 根据情况决定为 suffix 分配多少内存，以及在哪里分配内存。与另外一种更简单的分配方式（每个节点最多分配 15 个 suffix 的固定空间）相比，在短 key 场景下，这种方法能节省内存使用量约 16%，同时提升性能约 3% 。

value 存储在 link_or_value 这个 union 中，其中存储的可能是 value 或者下一层 B+ 树的指针。

mass tree 的性能主要却决于从 DRAM 获取树中节点的时延。 mass tree 在使用节点之前会并行预取节点的 cache lines ，这样节点在一个 DRAM latency 后就可以被使用。

这种情况下，访问一个大节点和访问一个小结点的时间是差不多的，但大节点的扇出更高，树的高度更低。在测试环境中，4 个 cache line（256 bytes，可以为扇出为 15）的树提供最好的性能。

mass tree 更新算法基于 B+ 树的更新算法。在一个满了的 border node 插入会导致分裂；如果在 border node 删除导致 border node 为空，则将其占用空间释放，同时从其父节点删除。经典的 B+ 树的算法在处理删除问题时，可能会对 key 进行重分布以维持平衡，但是直接删除在理论和实践中都有一些优势。

mass tree 最终的形状和数据分布有关。例如 1000 个 key ，如果它们共享 64 byte 的前缀，则 mass tree 至少有 8 层，但如果都不共享前缀，则只有 1 层。

mass tree 的查询复杂度和 B+ 树相同，但是对 range query 而言，mass tree 最坏情况下的查询复杂度要高一些，因为需要遍历多个 layer 。

算法

READ

read 操作不加锁，也不会操作任何共享数据结构。但为了防止 read 操作读到数据的中间状态，或者部分修改，读写之间需要有一些机制来处理这种情况。这种机制就是 节点的 version number，read 在进行读之前及读完后都会检查节点的 version number，来判断节点是否发生修改，如果发生修改 read 需要 retry；write 操作之前会先修改节点 version number，在插入 key 之前会设置 inserting 标记位，插入完成之后将 vinsert 加 1；split 操作之前先设置 splitting 标记位，完成后 vsplit 加 1。 version number 的 layout 如下图所示:

查找算法的伪代码如下：

INSERT & SPLIT

为处理 write-write 竞争，使用 fine-grained lock ，即节点锁，同一时刻只有一个线程能对当前节点进行写操作。

获取当前的 version number ，如果 inserting 或 splitting 标记位被设置，则 retry；

对节点加锁，设置  inserting 或 splitting 标记位 完成写动作；解锁，verinsert  或 vsplit 加 1 ，取消  inserting 或 splitting 标记位设置；

更新父节点。

UPDATE

update 操作用于修改一个已经存在的 key 的值，通过对齐的写入指令以原子的方式实现更新。对读操作而言，要么读到老的数据，要么读到新数据。因此 update 不需要更新 node 的 version number，也不需要 read 操作 retry 。

对于已经被 read 访问到的数据，如果要删除要等到 read 操作结束，垃圾数据清理通过 read-copy update 技术，是一种 epoch-based 回收机制。

BORDER NODE INSERT

传统的 B+ 树在叶子节点进行插入时，需要对 key 执行排列以达到有效，过程中节点会出现一些无效的中间状态。 

一种解决方式是强制重试，但是 mass  tree 用 permutation 字段使得插入操作可以在一个原子操作完成。permutation 字段可以表示 key 的顺序 以及 当前 key 的个数。通过 permutation  write 操作可以在一个对齐的写入，完成插入及排序工作。

读操作要么读不到新插入的 key ，要么读到且新 key 在正确的位置。不需要重新排列 key ，因此也不需要增加 version number。

permutation 是 64 位的，被分成 16 个 4 位区域。最低的四位是 nkeys ，表示节点内的 key 的数量，范围是 0 - 15 。剩余的 15 个 4 位 表示一个长度位 15 的数组， keyindex[15]。

permutation 的 layout 如下图所示，其中 keyindex[0] - keyindex[15] 存储 border node 中存在的 key 的索引，以 key 升序的方式。

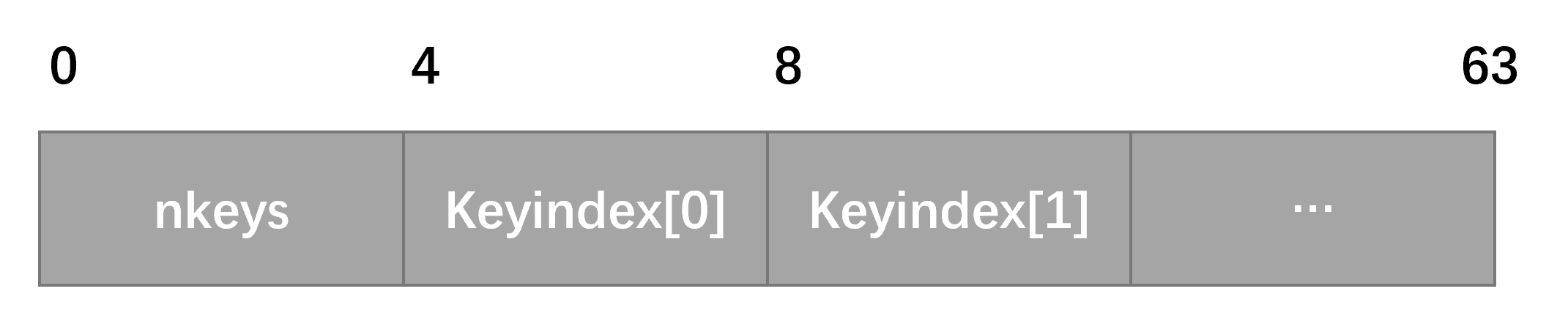
执行插入时，需要对节点加锁，然后加载 permutation，然后对 permutation 进行重排列，正确标记新插入的 key 正确的位置，然后增加 nkeys 的值；再将新的 key 和 value 写入之前没有使用的位置，最后一步将更新完的 permutation 回写，释放节点加的锁。只有在完成最后一步后，新的 key 对于 read 操作才是可见的。 这里需要注意，key 和 value 的写入，及 permutation 的回写需要设置编译器栅栏，以防止指令重排，影响执行顺序。

BORDER NODE SPLIT

分裂 border  node ，插入新 key；

生成一个新的 border node，原来的节点设置 splitting 位；拷贝 version number 到新生成的节点；

重新分配 key，插入新 key，完成分裂动作。

向上更新父节点。

SEARCH

查找包含某个 key 的 border node 算法如下：

获取正确的 root 节点，需要检查 isroot 位；

查找到 border node，返回；

否则查找包含 key 的子节点，如果检查到发生分裂，则从 root 节点开始重试；

向下查找，直到找到 border node。

DELETE

只讨论逻辑删除，物理删除需要额外的技术，比如 hazard pointer，epoch-based reclamation 等。

逻辑删除并不对 key 少的节点进行合并，当节点 key 减少到0时，需要标记这个节点为 deleted，然后将其从父节点删除，同时如果是叶节点的话，还需要维护叶节点的链接指针。

如果某棵子树为空的话也可以删除整棵子树。当其他线程发现节点处于 deleted 状态时，需要进行重试，因为这个节点逻辑上是不存在的。

另外需要处理一种特殊情况：

线程 1 查找 k1 找到位置 i，在读取 v1 前节点上 i 位置的 k1 被线程 2 删除；同时线程 2 在 j 位置插入了 k2 ；如果 i = j ，则可能线程 1 读到 v2 这个值。

为解决此问题，要在 i 被删除后重新插入时增加 vinsert 的值，然后线程 1 检查 version number 后进行重试。

实验数据

对比了 masstree 、MongoDB、VoltDB、Redis 和 memcached 的性能数据，基本上 mass tree 远超其他对比的数据库。

下图是对比数据，对比的是吞吐，单位是 百万请求/秒

另外，有人对比了 mass tree 和其他一些数据结构的性能，总体而言拥有非常不错的性能。

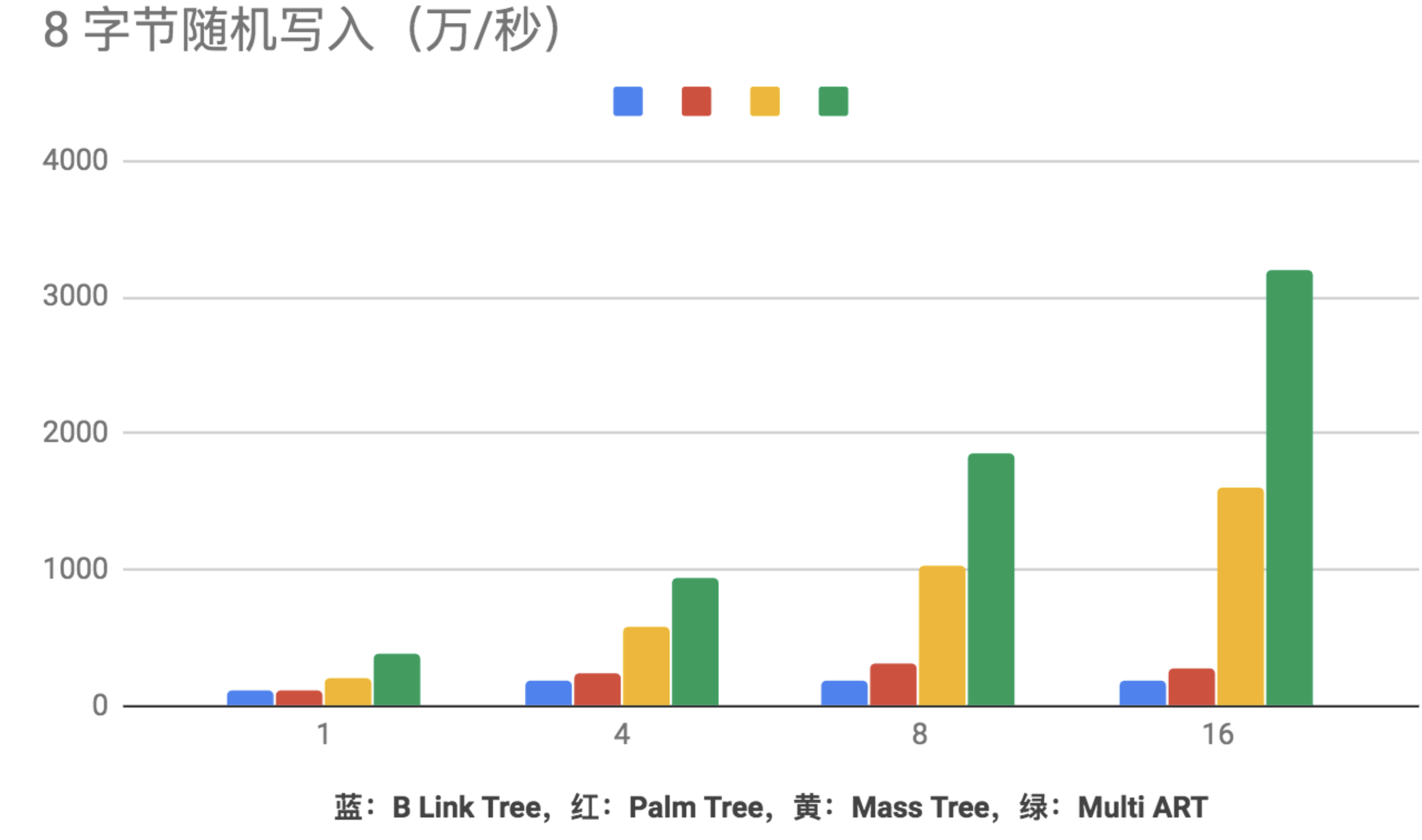
其他数据，不一一列举了

结论

1. mass tree 结构上Trie 和 B+ 两种索引树的结合。下降过程中的重试不需要从整棵树的根节点开始，同时可以加快拥有相同前缀的 key 的处理速度
2. 并发控制做了优化
3. 对树的流程做了优化，例如删除流程、写入流程等，其中用到了一些编程技巧，提高了性能
4. 单个节点存储的内容较少，减少了线程的竞争
5. 另外根据一些测试数据，对数的扇出做了调优，每个节点最大 15 个 key 实际是测试后得到的最优解。
6. 其他一些提升性能的点，例如 预取、key 的后缀管理等
7. mass tree 拥有突出的性能

参考文档：

https://pdos.csail.mit.edu/papers/masstree:eurosys12.pdf

https://www.bookstack.cn/read/aliyun-rds-core/729de3480e942857.md