你的 MySQL 表数据量是否满足本福特定律

很多情况下，我们会认为在一堆数据中，以 1 为首位的数字出现的概率为 1/9。然后实际情况却有些差异，原因就是存在本福特定律，今天就一起来聊聊这个有意思的话题。

本福特定律，也称为本福特法则，在一堆从实际生活得出的数据中，以 1 为首位的数字出现概率约为总数的 3 成，接近直觉得出的期望值 1/9 的 3 倍。通俗的讲，就是越大的数，以它为首的数出现的概率就越低。

在 b 进位制中，以 n 为首位的数字出现的机率为 logb(n + 1) − logb(n)

下表就是在十进制首位数字的出现机率（其中 d 为首位的数字，p 为出现的概率）

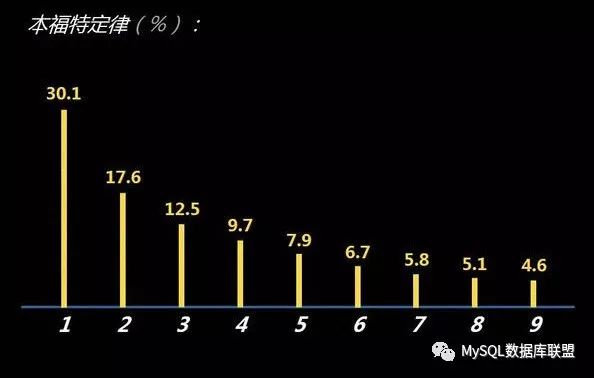
那么实际工作生活中，这些数字是否真的满足本福特定律呢？

我就拿某个业务所有的表数据量做了一次验证，其具体统计结果如下（其中一共有 541张表）：

发现基本满足本福特定律。

你验证一下你们自己的业务表数据量是否满足本福特定律？  

或者你们觉得身边其他哪些数据满足本福特定律？

欢迎在留言区讨论。

欢迎订购我的慕课网专栏《一线数据库工程师带你深入理解 MySQL》

专栏知识图如下（长按下图查看专栏详情）：

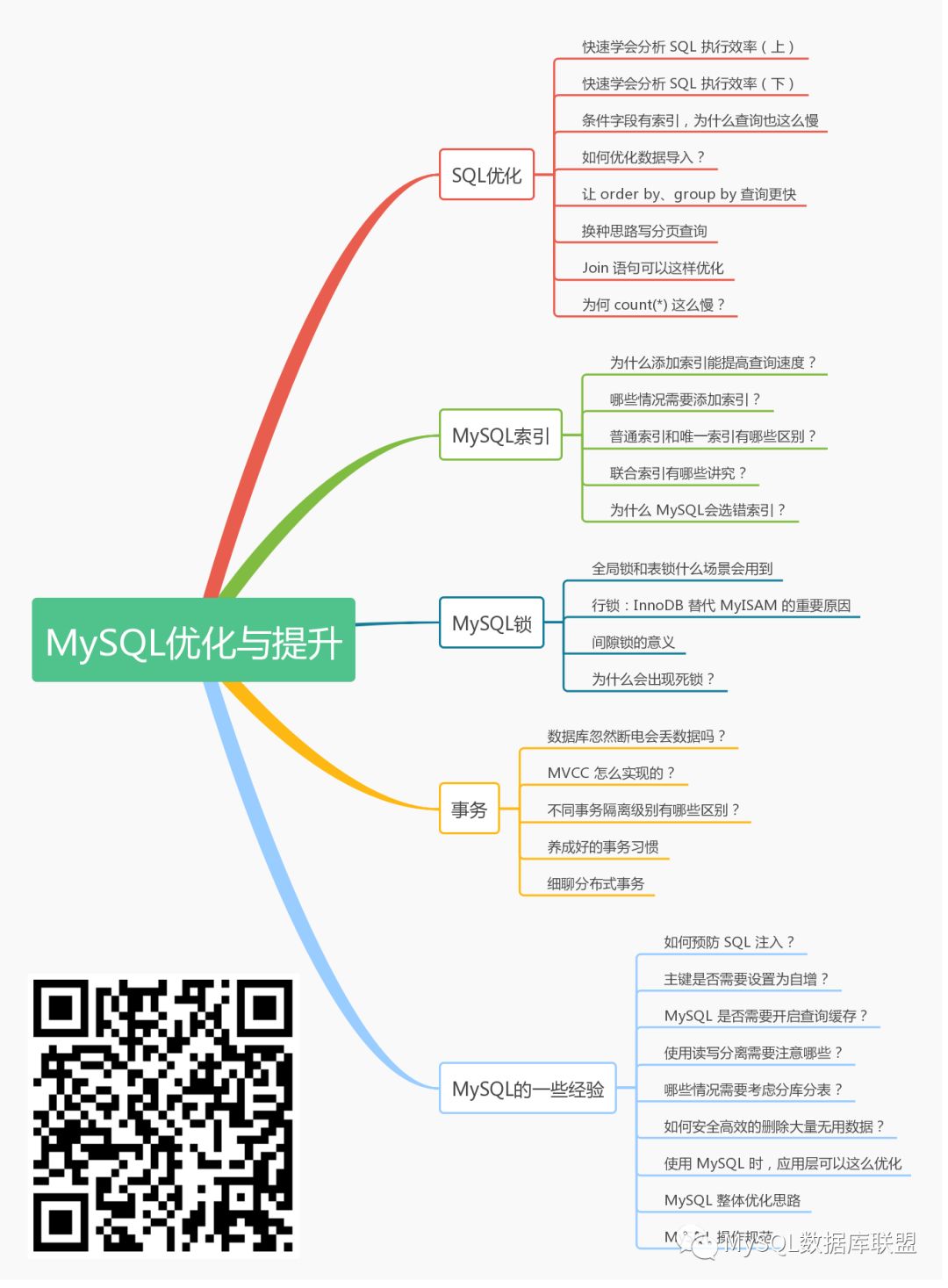
另外，我们创建了一个 MySQL 交流社群，围绕开发、运维、DBA、架构师和其他需要用到 MySQL 的群体，群内会不定期邀请一些身边的数据库大牛解答大家的问题，也会分享一些读书笔记、面试技巧等，同时也用于大家交流 MySQL 的学习技巧！

入群请加下方群秘二维码，回复 MySQL，等待群秘邀你入群。