编程任务
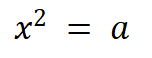
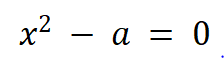
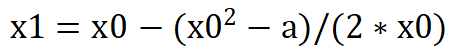
import math# 计算实数平方根的方程def f1(x,a):return x*x-a# 计算实数平方根方程的导函数def f2(x):return 2*x# 计算实数的平方根def sqrt(a):# x0为方程的初始值,作为方程的初始近似根x0 = a/2# 计算方程的下一个近似根x1x1 = x0 - f1(x0,a)/f2(x0);# 计算两个近似根x0和x1差的绝对值differ = math.fabs(x1-x0)# 循环计算方程的近似根,直至两个近似根差的绝对值小于1e-5while( differ >= 1e-5 ):# x0被赋值为x1x0 = x1# 计算方程的下一个近似根x1x1 = x0 - f1(x0,a)/f2(x0);# 计算两个近似根x0和x1的绝对差differ = math.fabs(x1-x0)return x1# 程序入口if __name__ == '__main__':a = input("请输入一个正实数:\n")print("%.5f" % sqrt(float(a)))
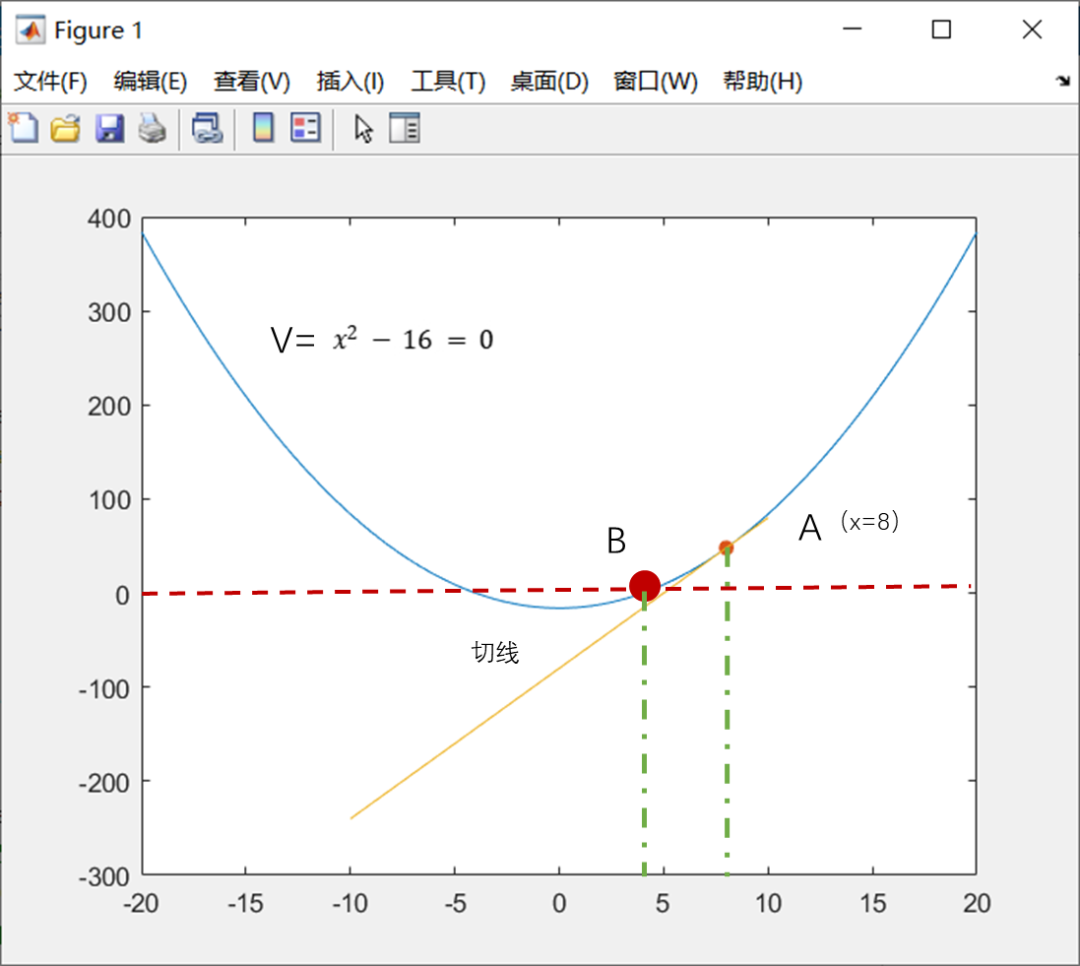
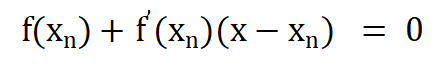
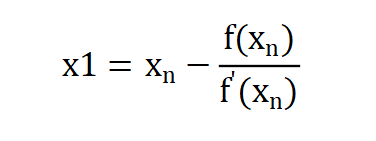
% 在区间[-1,1]内创建100个x坐标数据点x = linspace(-20,20,100);% 计算f(x)=x^2函数的y坐标y = x.^2-16;% 绘制曲线plot(x,y)hold on% 绘制曲线点(x=8)的切线draw_line(8,8*8-16)% 定义绘制切线函数function draw_line(x,y)% 绘制数据点scatter(x,y,'filled')% 计算函数y=x^2曲线(x,y)点的切线斜率k = 2 * xx1 = linspace(-10,10,100)% 通过切线方程计算y数据y1 = k*(x1-x)+y% 绘制切线plot(x1,y1)end
文章转载自编程实践楼,如果涉嫌侵权,请发送邮件至:contact@modb.pro进行举报,并提供相关证据,一经查实,墨天轮将立刻删除相关内容。






