Convolution与Deep Learning的相关背景
Convolution(卷积)是deep learning(深度学习)中的重要的操作,能进行同维变换,也能处理升维与降维。
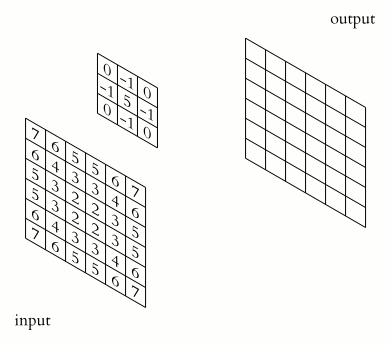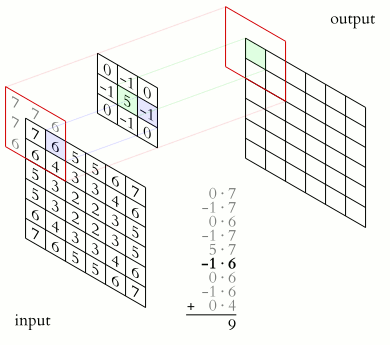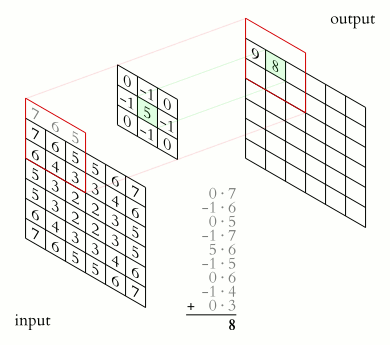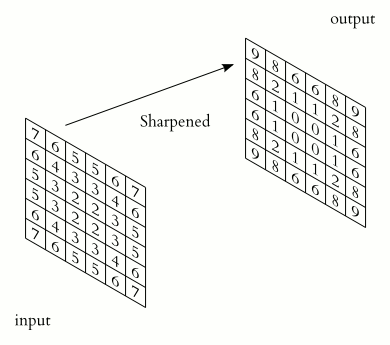
举个例子,看下图。每次在方格中找到1个点,再将周围的8个点加权,权重由另一个小方格(也称为kernel或filter)设定,最后把9个点的加权计算结果写到新的方格。
此图来自:https://commons.wikimedia.org
这种convolution方法在图片处理(如object detection)还有NLP等问题上有广泛的应用,因为图片中的每个像素点和周围的点有关系,一段文字中每个词也与前后的词有关系,而convolution正好是对应这种关系的有效数学工具。
Depthwise Separable Convolution
介绍完背景,有请主角Depthwise Separable Convolution隆重登场!在某些情况下,Depthwise Separable Convolution比传统convolution计算高效很多!
有些基于此的研究成果,比如:
Xception: Deep Learning with Depthwise Separable Convolutions
https://arxiv.org/abs/1610.02357
MobileNets: Efficient Convolutional Neural Networks for Mobile Vision Applications https://arxiv.org/abs/1704.04861
Depthwise Separable Convolution的精髓是Separable。不妨先从矩阵分解的角度去感性理解一下:3x3的矩阵可以分解成两个矩阵相乘,1x3和3x1。试想一下,matrix factorization就是这样成为一种collaborative filtering的有效数学工具。在convolution中,思想有神似,但具体操作差别甚大,且看下面分解。
传统的convolution处理图片
一张2维的图片有宽度(width, W)和高度(height, H),外加第3维颜色RGB(不妨称为深度depth)。我们可以定义M个filter,将图变换成 WxHxM 的3维数组,即M层的WxH图。
计算过程如下图所示:
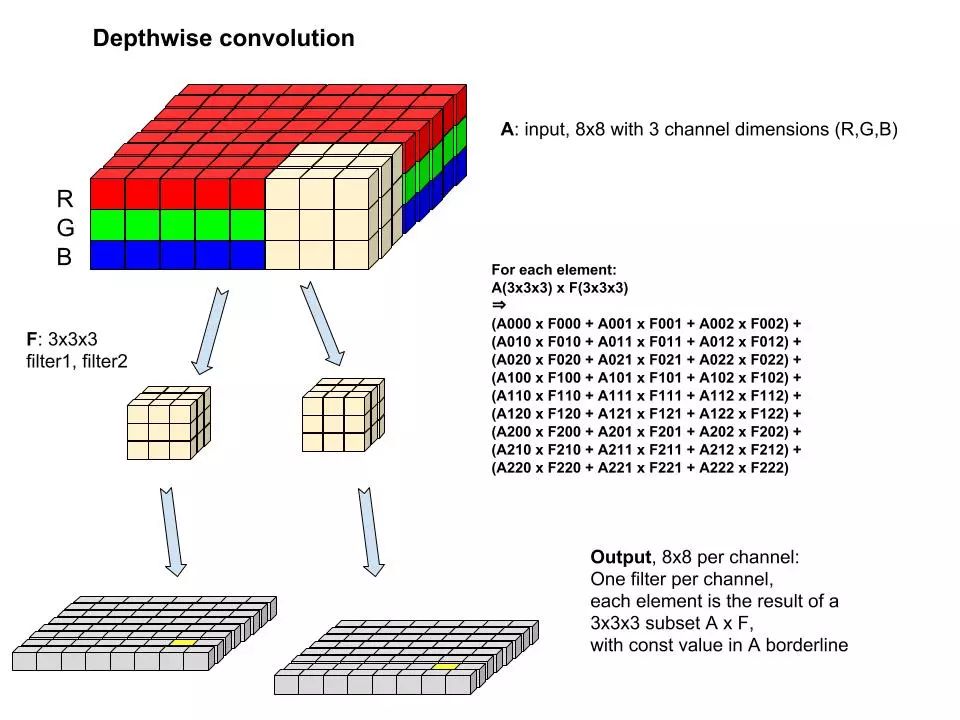
每个filter都是3x3x3的数组,通过逐格扫描原RGB图片,圈定周围格点3x3x3数组,能通过加权计算产生一个值,就是新层对应的点。
每层的格子数量与原图相同,M个filter产生M层。
记原图为变量Input,filter为变量F,w和h为格子的位置,around()为2维空间周围8点及中心点本身(显然,around()和F的维数完全相同),则
Output[w, h]
= sum( around(Input[w, h]) * F )
这里的*不是矩阵相乘,而是数组的各位置相乘,比如
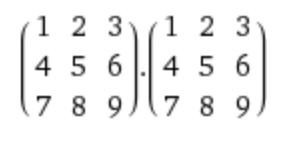
在这里的结果如下,相当于是numpy.multiply()

而不是矩阵相乘,即numpy.matmul()

比如 30 = 1*1 + 2*4 + 3*7
如果filter是3x3x3,那M个filter的计算复杂度为
3x3x3xWxHxM
= (3x3xM) x (WxHx3)
Depthwise separable convolution处理图片
依然是相同的RGB图片WxH,要将其变换成WxHxM的数组。
操作过程如下:
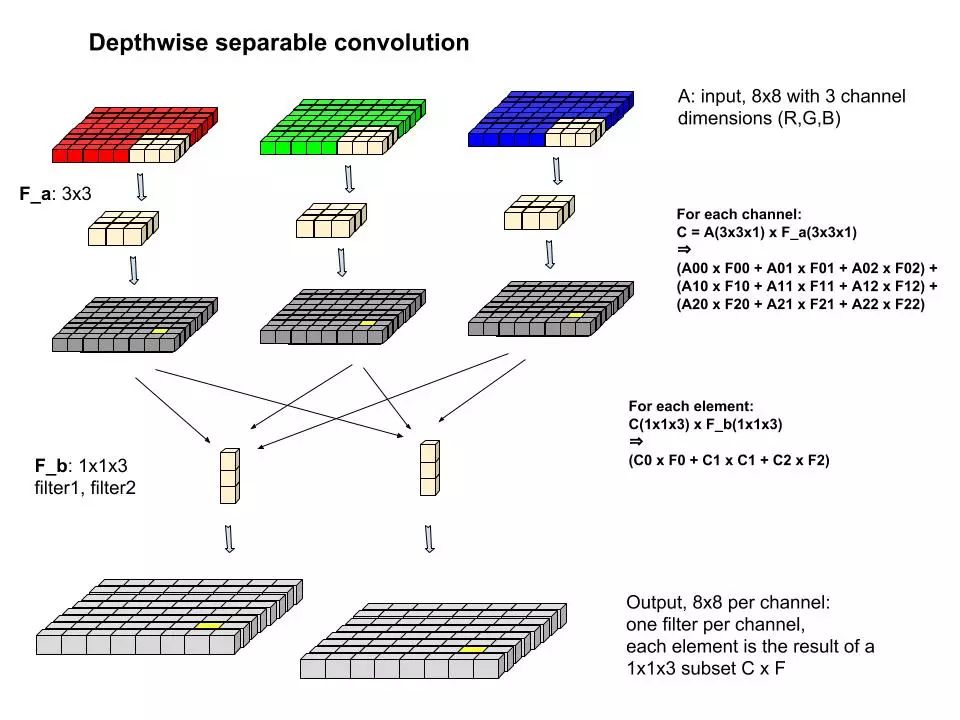
首先将图片分为R、G、B三层分开计算,每层都对应一个3x3的2维filter(记为F_a),逐格扫完后,生成另一个WxH的数组(3层分别记为C_r, C_g, C_b);
然后进行第二轮filter(记为F_b)操作,一共M个F_b,每个维数为1x1x3,逐格扫描C,分别与每层的点作加权
Output[w, h]
= C_r[w, h]*F_b[0] + C_g[w, h]*F_b[1] + C_b[w, h]*F_b[2]
举个例子,为了篇幅显示方便,如果C为2x2(可以为任意维数),C_r, C_g, C_b分别为
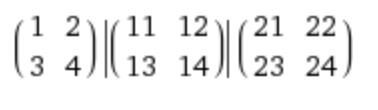
F_b为 [2, 1, 0.01]
则计算过程为

Output等于

如果filter是3x3x3,那M个filter的计算复杂度为
第一阶段:3层,每层为3x3xWxH
第二阶段:3xWxHxM
总共
3x3xWxHx3 + 3xWxHxM
= (3x3+M) x (WxHx3)
如果W = 1024, H = 1024, M = 32
传统Depthwise Convolution:
(3x3xM) x (WxHx3)
=> (3x3x32) x (1024x1024x3)
=> 864 x 2^20
Depthwise Separable Convolution:
(3x3+M) x (WxHx3)
=> (3x3+32) x (1024x1024x3)
=> 123 x 2^20
当M为32的时候,传统算法是Separable算法的7倍。
计算复杂度的随着M的变化如下

在TensorFlow和Keras中,有Separable Convolution的实现,参考https://www.tensorflow.org/api_docs/python/tf/keras/layers/SeparableConv2D






