算法面试汇总（三十七）

Coding的哔哔叨叨 2021-01-26

312

👉👀💬今日练习（一）盛水最多的容器（LeetCode-11）。给定一个ight数组，下标间的距离为宽，数组元素为高，求的能装能装最多多少水。举例：

输入：[1,8,6,2,5,4,8,3,7]
输出：49

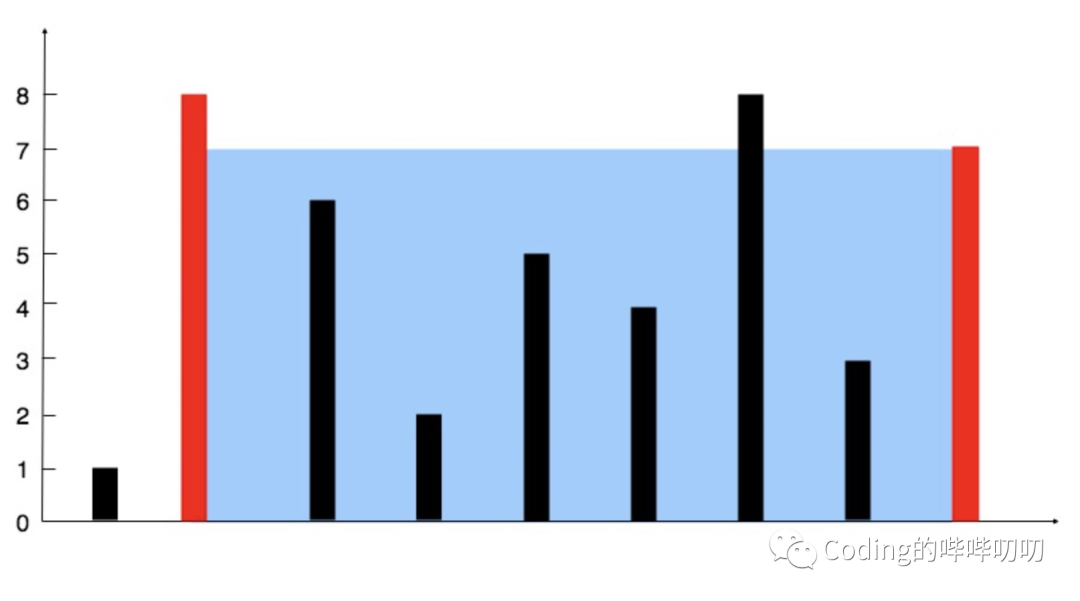
🙇思路：

这道题很容易和我们之前做过的接雨水的题混淆，动态规划啥的对这道题帮助不大，这道题要想在O(N)的时间内完成，双指针是最佳选择。

从数组两端开始，指针向中间移动（left++、right--），且循环条件为left<right，严格小于。

当height[left]<height[right]时，left++；
否则，right--；
在循环过程中记录桶间的盛水量；
注意盛水多少是由最短的柱子决定的。

代码：

public int maxArea(int[] height) {
    int len=height.length;
    if(len<2){
        return 0;
    }
    int left=0;
    int right=len-1;
    int res=0;
    while(left<right){
        res=Math.max(res,(right-left)*Math.min(height[left],height[right]));
        if(height[left]<height[right]){
            left++;
        }else{
            right--;
        }
    }
    return res;
}

👉👀💬今日练习（二）寻找两个正序数组的中位数（LeetCode-4）。给定两个正序组，找出两个数组的中位数，要求在O(log(n+m))内完成。举例：

输入：nums1=[1,3],nums2=[2]
输出：2
解释：合并后数组为：[1,2,3]，所以中位数为2


输入：nums1=[0],nums2=[3]
输出：1.5
解释：合并后数组为：[0,3]，所以中位数为1.5

🙇思路：

这道题，如果是没有时间的限制，其实我们是很轻易就可以计算出中位数的(比如合并两个数组，并使之有序，然后取出中位数)，但题目要求在O(log(m+n))内完成，这一下，此题的难度就上升了一个档次，不过也不要怕，看到O(log(m+n))，我们应该是很容易联想到二分的思路，没错，这道题确实就是二分来做，不过需要有一些思路的变化，下面开始此题的思路解析。

这题要求中位数，我们可以把这个问题转化一下，转化成求数组中的第k个数，这儿先不要考虑数组长度的奇偶，因为数组若为奇数则第k个数就是中位数，如果是偶数则中位数是第k个和第k+1个数的平均值，但在求第k或k+1个数的过程是一样的。

好了，到这儿我们就把问题转化成了：求有序数组中的第k个元素。

这里我们以nums1=[1,3,4,9]和nums2=[1,2,3,4,5,6,7,8,9,10]，来举例说明求解过程。

在两个数组中比较第k/2个数，假设nums1[k/2]<nums2[k/2]，说明第k个数一定不在nums1的前k/2个数中，这样我们便排除的了k/2个数了，如上面给出的两个数组，按照问题转换，我们要求的第7个数，k/2=3，nums1第三那个数是4，nums2第3个数是3，3<4，所以nums2中的前3个数，1,2,3很显不在我们要求的第7个数的范围内，所以可以排除掉3个数。

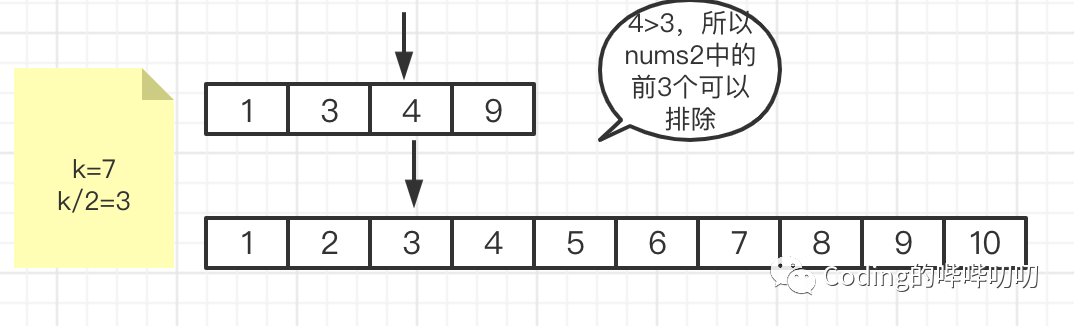
由于我们已经排除掉3个数，所以k的值也要顺势减3，变成在剩下的元素中找第4大的元素，继续比较两个数组中的第k/2大的数，3<5，所以将nums1中的前k/2个数可以排除，所以有排除1，3这两个数。新的k为2。沿着这个思路继续做，直到k==1。

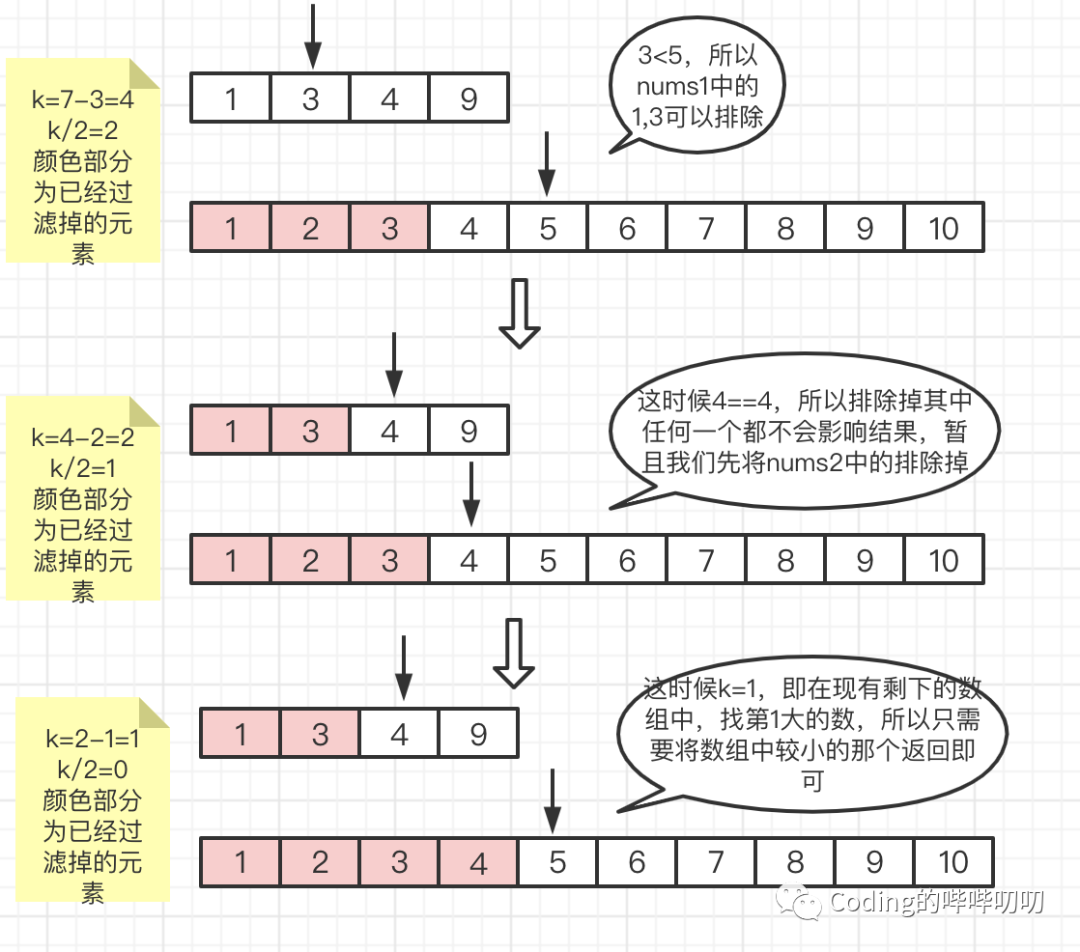
所以最终返回的结果是4（这里我们还没有对数组总长度的奇偶做处理）。

上面的处理过程，还有一种特殊情况我们需要考虑，那就是如果k/2超过了其中一个数组的长度，这时候我们只需要返回另外一个数组中此时的第k大的元素即可。

可能上面文字逻辑有点繁琐，大家可结合下面代码来加深理解。

代码：

public double findMedianSortedArrays(int[] nums1, int[] nums2) {
    int length1=nums1.length;
    int length2=nums2.length;
    //取中位数，加1除2
    int k1=(length1+length2+1)/2;
    double d1=getKdata(nums1,0,length1-1,nums2,0,length2-1,k1);
    int k2=(((length1+length2)&1)!=0)?-1:k1+1;
    if(k2 <0){
        return d1;
    }
    double d2=getKdata(nums1,0,length1-1,nums2,0,length2-1,k2);
    return (d1+d2)*0.5;
}
private double getKdata(int[] nums1, int i1, int e1, int[] nums2, int i2, int e2,int k) {
   int l1=e1-i1+1;
   int l2=e2-i2+1;
   if(l1>l2){
       return getKdata(nums2,i2,e2,nums1,i1,e1,k);
   }
   //如果其中一个数组都已被排除，直接返回另一个数组的第[i2+k-1]位置的数。
   if(l1==0){
       return nums2[i2+k-1];
   }
   //如果k==1，返回两个数组中i1、i2位置中较小的那个
   if(k==1){
       return Math.min(nums1[i1],nums2[i2]);
   }
   int i= i1+Math.min(l1,k/2)-1;
   int j= i2+Math.min(l2,k/2)-1;
   //判断两个数组中第k/2个元素的大小。
   if(nums1[i]>nums2[j]){
       //如果nums1[i]>nums2[j], 则将nums2中的k/2位置前的都过滤掉,
       //重新计算k，新的k为原k减掉这次过滤掉的个数
       return getKdata(nums1,i1,e1,nums2,j+1, e2,k-(j-i2+1));
   }else{
       return getKdata(nums1,i+1,e1,nums2,i2,e2,k-(i-i1+1));
   }
}

不积跬步，无以至千里。

文章有帮助的话，点个转发、在看呗。
谢谢支持哟 (*^__^*)

END

👇

面试

文章转载自Coding的哔哔叨叨，如果涉嫌侵权，请发送邮件至：contact@modb.pro进行举报，并提供相关证据，一经查实，墨天轮将立刻删除相关内容。

算法面试汇总（三十七）

评论