算法-动态规划（一）

        临时插入一个知识点，关于算法中常用的动态规划的专题。

       动态规划的问题在日常的算法中应用的地方还挺多，所以想集中一个专题来练习和总结一下动态规划的问题。

• 动态规划

  ---

        啥子是动态规划？能解决什么问题，先来看张关于动态规划问题思考方向的图。

        动态规划的「规划」就是填表的意思，我们下面的应用也就能看出来。是一种以空间换时间的做法。

        动态规划的「动态」是自低而上，不同于我们之前做过的”递归+记忆化“的方式，这是一种自顶而下的方式，我们直接对问题求解，如果遇到新的问题，我们就记录一下，下次再遇到同样的问题就直接读取，这个叫自顶而下。而动态规划是自低而上。

        ”自低而上“就是说我们知道问题原本的样子，然后我们一步步计算中间的过程，最后得到要求问题的解。

        动态的思想的思想就在于我们不直接面对要解决的问题，而是站在上帝视角，直接给出答案。

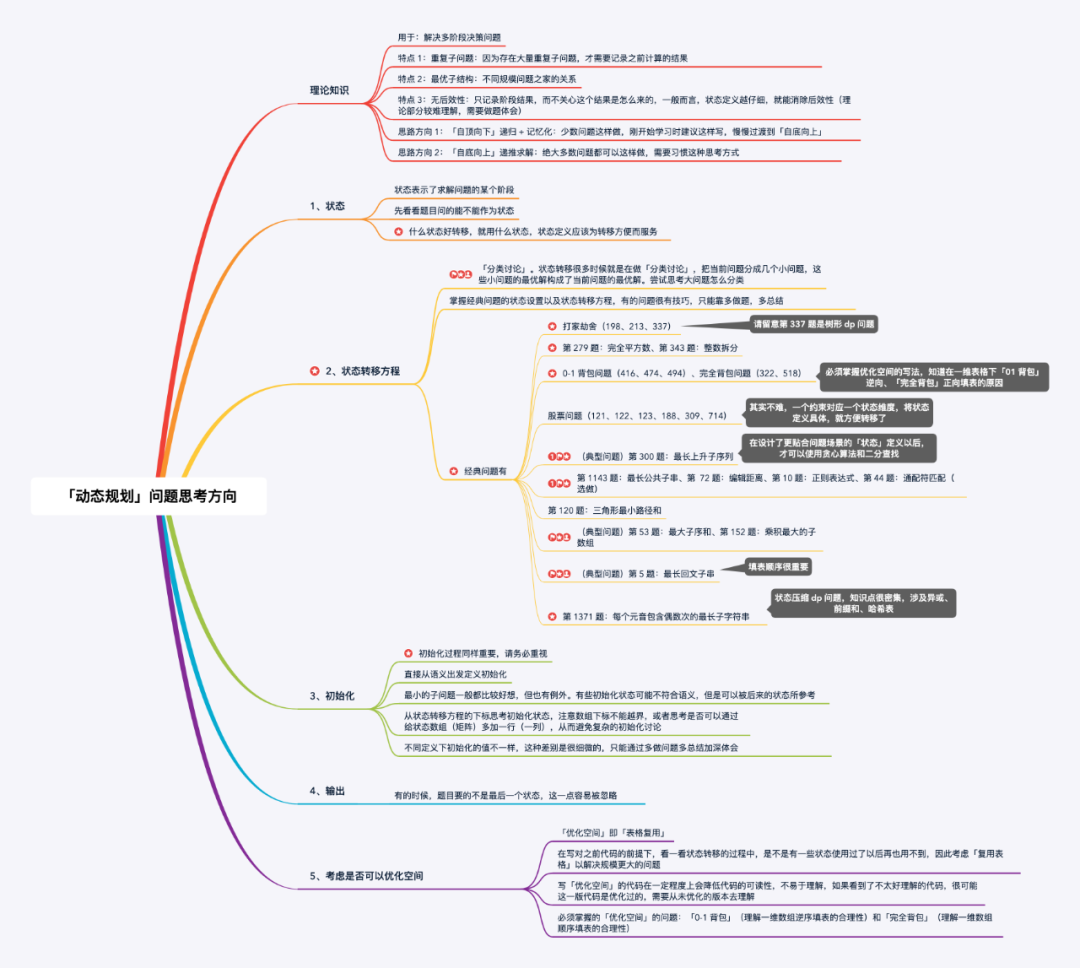
        动态规划最重要的就是状态转移，也是这个算法思想的难点，常见的推导理论有：

1. 分类讨论，即对状态空间进行分类；

2. 归纳「状态转移方程」是一个很灵活的事情。

        不管说多少，最重要的还是练，其实我对这个玩意儿也不是很清晰，题海战术练吧，我也是最近做了几道题，感觉有点头绪了，写个专题记录一下。

👉👀💬今日练习（一）最长回文子串（LeetCode-5）。

给定一个字符串s，找出s中最长的回文串。如：

输入：abaab
输出：baab

🙇思路：

        上面我们提过，动态规划的一个最主要的问题就是状态转移，而「回文」，是天然具备了「状态转移」的性质。下面我们来展开讨论一下：

• 一个回文字符串，如果去掉最外边的两个元素，剩下的元素依旧是回文。

• 如果去掉最外边两个元素，剩下的字符串不是回文，那么整个字符串一定不是回文，也就没有继续进行的必要了。

• 所以，如果最外边的两个元素同等，那么剩下的字符串的回文性质决定整个子串的性质。这个就是状态转移。因此可以把「状态」定义为原字符串的一个子串是否具有回文特性。
  

具体的做法如下：

1. 定义状态，我们用一个二维数组res[i][j]来记录字符串s[i,j]是否为回文串。

2. 状态转移。
   

1. 根据我们上面对回文串的分析，可以得到：

   res[i][j]=(s.charAt(i)==s.charAt(j)) && res[i+1][j-1]。
   

3. 边界值讨论。

1. 对于res[i+1][j-1]的边界值，必须得是能构成一个区间，所以可以轻易得到，如果(j-1)-(i+1)<1，则一定不构成区间，整理得到：j-i<3。

2. 对上面推导出的j-i<3不构成区间进行论证，j-i<3，即去掉两头后剩下的中间子串长度小于2，可分为下面两种情况：

1. 如果子串s[i+1 , j-1]只有一个字符串，显然s[i,j]一定是回文。

2. 如果子串s[i+1 , j-1]为空串，那s[i,j]一定也是回文（基于我们上面2.的论证）。

3. 所以，当s.charAt(i)==s.charAt(j)&&(j-i<3)成立的情况下，我们就可以直接下结论s[i,j]是回文。即res[i][j]=true。

代码：

public  String longestPalindrome_4(String s) {
    int len=s.length();
    if(len < 2){
        return s;
    }
    int maxLen=1;
    int beg=0;
    boolean[][] res = new boolean[len][len];
    for(int i=0;i<len;i++){
        res[i][i]=true;
    }
    for(int j=1;j<len;j++){
        for(int i=0;i<j;i++){
            if(s.charAt(i)!=s.charAt(j)){
                res[i][j]=false;
            }else{
                if(j-i<3){
                    res[i][j]=true;
                }else{
                    res[i][j]=res[i+1][j-1];
                }
            }
            if(res[i][j] && (j-i+1>maxLen)){
                maxLen=j-i+1;
                beg=i;
            }
        }
    }
    return s.substring(beg,beg+maxLen);
}

复杂度分析

• 时间复杂度：O(N^2)，有两层循环。

• 空间复杂度：O(N^2)，我们需要用一个二维空间来保存一个状态值。

解法二：中心扩散法。

🙇思路：

        此题还有一种空间复杂度好点的算法，当然这不是我们此专题的重点，我仅是拿来记录一下。

        下面对中心拓展法进行说明：

         中心拓展法，也就是说，我们从字符串的中间开始向外扩散，符合回文串的条件下能扩散多远就扩散多远，最终找到那个扩散最长的子串。

        在扩散的过程中，我们需要注意字符串长度为奇数和偶数的情况。字符串的中心是不一样的。如：

• "aba"中心是"b"。

• "abba"中心是"bb"中间的空隙。

  所以我们需要对这两种情况都进行考虑。

代码：

public  String longestPalindrom_5(String s) {
    int len=s.length();
    if(len < 2){
        return s;
    }
    String res=s.substring(0,1);
    for(int i=0;i<len-1;i++){
        String oddStr=helper(s,i,i);
        String evenStr=helper(s,i,i+1);
        String maxStr = oddStr.length()>evenStr.length()?oddStr:evenStr;
        if(maxStr.length()>res.length()){
            res=maxStr;
        }
    }
    return res;
}
private String helper(String str,int left,int right){
    while (left>=0 && right<str.length()){
        if(str.charAt(left) == str.charAt(right)){
            left--;
            right++;
        }else {
            break;
        }
    }
    // 这儿要注意left和right位置的元素都不能要，
    // 一是因为进入循环前，left和right位置的元素就不等，
    // 二是因为最后一次循环后left和right的值进行了加减才得到下一次扩散的位置退出了循环
    return str.substring(left+1,right);
}

复杂度分析

• 时间复杂度：O(N^2)，有两层循环。

• 空间复杂度：O(1)，我们只用到了常数个临时变量，且与字符串长度无关。

不积跬步，无以至千里。

文章有帮助的话，点个转发、在看呗。
谢谢支持哟 (*^__^*)

👇