Dijkstra(迪杰斯特拉)算法是计算在有向图中从单原点到其他顶点的最短路径问题。
算法
基本思路是,按路径长度递增的顺序产生最短路径。
已知有向图定点集合(V[0], V[1], V[2], ..., V[n]),和边权值map[i][j]表示从顶点V[i]到顶点V[j]的长度(如果V[i]到V[j]能联通,则是边的直接权值,如果不能联通则是无穷大Inf),求从原点V[0]到其他节点的最短了路径。
步骤:
1. 把有向图的所有定点V分成两组:
S :表示已经求出最短路径的顶点集合。
T :表示尚未求出最短路径的顶点集合
初始状态S为空,T为V-V[0]={V[1], V[2], V[3], ..., V[n]}。
2. 找出T中从V[0]开始最短路径最小的顶点(有说这是贪心算法),记为V[k]
把V[k]从T中移出,然后加入到S中。
然后对T中顶点的dist数组值进行修正。
因为加入了新的中间节点V[k],判断经过新的中间节点V[k]之后,dist[i]值是否会比原来不经过这个中间节点V[k]小。
即,dist[i] = min(dist[i], dist[k]+map[k][i])
3. 重复2直到T为空为止。
算法理论依据:
从顶点V[0]到V[k]的最短路径,是下面两个值的较小者:
是从V[0]到V[k]的直接路径的权值。
是从V[0]经过S中顶点S[m],然后加上S[m]到V[k]的直接路径的权值。
经过S中有顶点到达V[k]的路径有多条,取权值最小的一条。
算法缺点:
边的权重不能是负数。
只能处理单原点的最短路径,也就是从固定一个点到其他顶点的最短路径,不能处理任意两个顶点的最短路径。
当然可以通过不停的调用Dijkstra算法,以期达到任意顶点之间的最短距离。
代码实现:
下面给出一个c语言的算法实现;例子采用7个节点的一个有向图,如下:
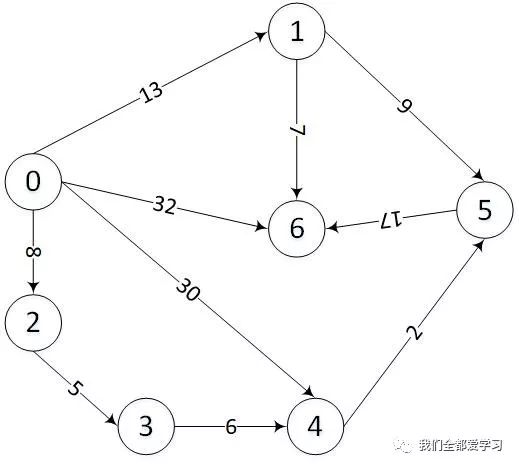
实现中定义三个数组变量:
distance[n]:用来存储从0节点到其他节点的最短路径。
如果一个节点已经处在S集合中,那么此时distance[i]就是从开始0节点到i节点的最短路径长度。
如果一个节点还是处在T集合中,那么此时distance[i]的值还不一定是最终的最短路径,可能是中间长度,在后续的计算调整中会逐步变成最短路径值。
prepath[n]:表示从开始0节点到i节点的最短路径中,排在i节点前面的那个节点;这个数组用来输出打印路径中的节点序列使用。
visited[n]:表示节点是否已经处理过了,如果等于true,那么节点已经放入S集合,即已经找出了最短路径,否则还在T集合里面。
#include <stdio.h>
void dijkstra(unsigned int map[][7], int n) {
int distance[n]; the intermediate and final distance from node[0] to node[i]
int prepath[n]; // the prefix node of node[i] in its path
int visited[n]; // whethere node[i] has finished, i.e., found out the shortest path
initialize
for (int i = 1; i < n; i++) {
distance[i] = map[0][i];
prepath[i] = 0;
visited[i] = 0;
}
// major loop
for (int r = 1; r < n; r++) {
unsigned min_dist = -1;
int min_idx = -1;
find out the minimun distance value from V set
for (int i = 1; i < n; i++) {
if (visited[i] == 0 && distance[i] <= min_dist) {
min_dist = distance[i];
min_idx = i;
}
}
//printf("======== Round: %d ========\n", r);
printf("distance S : "); for (int i = 1; i < n; i++) { if (visited[i] != 0) printf("[%d]=%d ", i, distance[i]); } printf("\n");
/printf("distance T : "); for (int i = 1; i < n; i++) { if (visited[i] == 0) printf("[%d]=%d ", i, distance[i]); } printf("\n");
//printf("pick min_idx: %d, min_dist: %d\n", min_idx, min_dist);
// mark node[min_idx] as visited, i.e,. put to S set from T set
visited[min_idx] = 1;
// update distance value for V set node
// for each node in V set, compare the path:
// distance[i] vs. distance[min_idx] + map[min_idx][i]
for (int i = 1; i < n; i++) {
if (visited[i] == 0 && map[min_idx][i] != -1 && min_dist + map[min_idx][i] < distance[i]) {
distance[i] = min_dist + map[min_idx][i];
prepath[i] = min_idx;
}
}
}
// print final output, distance value and path
for (int i = 1; i < n; i++) {
printf(" distance[%d]: %d,\treverse path: %d", i, distance[i], i);
int j = prepath[i];
while (j != 0) {
printf("<-%d", j);
j = prepath[j];
}
printf("<-%d\n", 0);
}
}
int main() {
unsigned int map[][7] = {
// 0 1 2 3 4 5 6
//---+-------------------------
/*0*/{ 0, 13, 8, -1, 30, -1, 32},
/*1*/{ -1, 0, -1, -1, -1, 9, 7},
/*2*/{ -1, -1, 0, 5, -1, -1, -1},
/*3*/{ -1, -1, -1, 0, 6, -1, -1},
/*4*/{ -1, -1, -1, -1, 0, 2, -1},
/*5*/{ -1, -1, -1, -1, -1, 0, 17},
/*6*/{ -1, -1, -1, -1, -1, -1, 0},
//-----------------------------
};
dijkstra(map, 7);
}
编译测试:
distance[1]: 13, reverse path: 1<-0
distance[2]: 8, reverse path: 2<-0
distance[3]: 13, reverse path: 3<-2<-0
distance[4]: 19, reverse path: 4<-3<-2<-0
distance[5]: 21, reverse path: 5<-4<-3<-2<-0
distance[6]: 20, reverse path: 6<-1<-0






