一.主成分的说明
主成分的主要目的是希望用较少的变量去解释原来资料中的大部分变异,即希望能将手上许多相关性高的变量转化为彼此互相独立的变量,能由其中选取原始变量个数少的,能解释大部分资料变异的几个新变量,也是所谓的主成分,而这几个主成分也就成为我们用来解释资料的综合性指标。
接下来举个例子来说明吧
15名学生的身高x1和体重x2的数据,我们来探索一下数据
x1<-c(147,171,175,159,155,152,158,154,164,168,166,159,164,177)
> x2<-c(32,57,64,41,38,35,44,41,54,57,49,47,46,63)
> cor(x1,x2)
[1] 0.9672073
> plot(x1,x2,xlim = c(145,180),ylim = c(25,75))
> lines(c(146,178),c(30,60),lwd=2)
> lines(c(163,166),c(54,57))
> library(shape)
> lines(getellipse(24,3,mid=c(162,48),angle=48),lty=3)
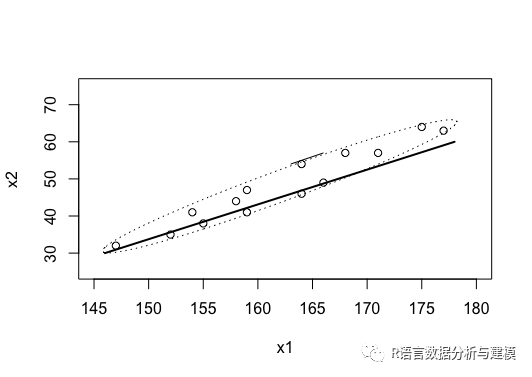
这个二维椭圆有两个主轴,有几个变量,就有几个主成分。那么如何来判断是否是主成分呢?这里的方式是看这些被选的主成分的主轴的长度占所有主轴总长度之和的80% 左右即可。
二.主成分的分析的主要过程:
主成分的计算:
(1)根据princomp()函数来计算主成分对象
(2)方差贡献率:计算方差贡献率(proportion of variance)与累积方差贡献率(cumulative proportion)
(3)主成分的个数,根据累积贡献率大于80%确定主成分的个数
2.主成分的得分图:
(1)主成分得分:comp.j=aj'x
(2)主成分得分图:若取m=2,则将每个样品的p个变量代入上式即可计算出每个样品的主要成分comp.1和comp.2,并将其在平面上做主成分得分的散点图,进而对样品进行分类或对原始数据进入更深入的研究。
3.综合得分及排名
(1)综合得分:以各成分方差贡献率为权,求加权。
(2)得分排序:利用总得分进行综合排名
4.进行主成分分析
三.主成分分析的注意事项:
1.主成分分析可以样本协方差或相关系数矩阵为出发点进行分析
2.为了使方差最大,通常主成分分析是做转轴的
3.成分的保留:kaiser主张将特征值小于1的成分因子放弃,而保留特征值大于1的成分
4.在实际研究中,研究者如果能有不超过3个成分解释变异的80%,就算令人满意。
5.使用主成分后,会使得各方差变大,而且各变量之间会彼此独立。
(这个内容相对简单,就不po案例了,等到具体项目在介绍)






