基于R语言的判别分析：fisher判别法，距离判别法以及Bayers判别法（附源代码）

判别分析（Discriminat Analysis)是多变量统计分析中用于判别样本所属类型的一种统计分析法。它所要解决的问题是在一些已知研究对象用某种方法已经分成若干类的情况下确定新的样本属于已知类别的哪一类。判别分析在处理问题时，通常要给出一个衡量新样品与各已知类型接近程度的描述统计模型即判别函数，同时也指定一种判别规则，借以判定新的样本归属。

判别分析的种类主要分为确定型判别：Fisher判别法（1）   线性型 （2）距离型（3）非线性型  还有一类是统计型判别：Bayers 判别法（1）概率型 （2）损失型

一 .接下来我们来看看Fisher 线性判别函数                （来源于网络）

两个总体中抽取具有p个指标的样品观测数据，借助于方差分析的思想构造一个线性判别函数：

其中系数

确定的原则是使两组间的组间离差最大，而每个组的组内离差最小 [2] 。

当建立了判别式以后，对一个新的样品值，我们可以将他的p个指标值代人判别式中求出Y值，然后与判别临界值比较，就可以将该样品归类。设有2个总体

，其均值和协方差矩阵分别是

和

。可以证明，Fisher判别函数系数

设从第一个总体

取得

个样本，从第二个总体

取得

个样本，记两组样本均值分别为

，样本离差阵为

。显然，

的无偏估计为

。

的估计有两种方式。

判别函数为

第二种估计方式是联合估计

于是判别函数

当

时，两种方法是等价的；当

与

相差不大时，两种方法近似；当

与

相差很大时两种方法相差较远。目前采用较多的是第二种方法 [2] 。

po个案例：雨天和晴天的温度差和湿度差                         

(1)建立判别函数：  

group<-c(1,1,1,1,1,1,1,1,1,1,2,2,2,2,2,2,2,2,2,2)

x1<-c(-1.9,-6.9,5.2,5.0,7.3,6.8,0.9,-12.5,1.5,3.8,0.2,-0.1,0.4,2.7,2.1,-4.6,-1.7,-2.6,2.6,-2.8)

x2<-c(3.2,0.4,2.0,2.5,0.0,12.7,-5.4,-2.5,1.3,6.8,6.2,7.5,14.6,8.3,0.8,4.3,10.9,13.1,12.8,10.0)

library(MASS);

weather<-lda(group~ x1 + x2);

weather

结果如下：

Prior probabilities of groups:

  1   2 

0.5 0.5 

Group means:

     x1   x2

1  0.92 2.10

2 -0.38 8.85

Coefficients of linear discriminants:

          LD1

x1 -0.1035305

x2  0.2247957

                                                                           (2)判别函数对源数据进行检测    

weatherPredict<-predict(weather)

newGrop<-weatherPredict$class

cbind(weather$group,weatherPredict$x,newGrop)

结果如下：                                                                 

LD1 newGrop

1  -0.28674901       1

2  -0.39852439       1

3  -1.29157053       1

4  -1.15846657       1

5  -1.95857603       1

6   0.94809469       2

7  -2.50987753       1

8  -0.47066104       1

9  -1.06586461       1

10 -0.06760842       1

11  0.17022402       2

12  0.49351760       2

13  2.03780185       2

14  0.38346871       2

15 -1.24038077       1

16  0.24005867       2

17  1.42347182       2

18  2.01119984       2

19  1.40540244       2

20  1.33503926       2

(3)构造混淆矩阵，计算判对率

tab<-table(group,newGrop)

tab

sum(diag(prop.table(tab)))

结果如下 ：

> tab<-table(group,newGrop)

> tab

     newGrop

group 1 2

    1 9 1

    2 1 9

> sum(diag(prop.table(tab)))

[1] 0.9

> 

(4).对新数据进行预测：

当x1=9，x2=3时候进行判断

predict(weather, newdata = data.frame(x1 = 9, x2 =3))                                                                      结果如下：

$class

[1] 1

Levels: 1 2

$posterior

          1          2

1 0.9177512 0.08224878

$x

        LD1

1 -1.460191

即当新=9，x2=3时候，类别为1，说明是下雨的天气。

当x1=-1,x2=11时候

predict(weather, newdata = data.frame(x1 = -1, x2 =11))                                                                     

predict(weather, newdata = data.frame(x1 = -1, x2 =11))

$class

[1] 2

Levels: 1 2

$posterior

           1         2

1 0.09372864 0.9062714

$x

      LD1

1 1.37348

  即当x1=-1，x2=11时候，类别为2，说明是晴天的天气。  

二.距离判别法

根据已知分类的数据，分别计算各类重心即各组的均值，判别准则是对任一给的一次观测，若从与第i类重心距离最近，就认为它来自i类。

其中又可以分为两个距离判别和多总体距离判别

对上面案例再次引用

qd=qda(group~x1+x2)

qd

结果如下：

> qd=qda(group~x1+x2)

> qd

Call:

qda(group ~ x1 + x2)

Prior probabilities of groups:

  1   2 

0.5 0.5 

Group means:

     x1   x2

1  0.92 2.10

2 -0.38 8.85

(2).预测新的数据

qd<-predict(qd)

g2<-qd$class

data.frame(group,g1,g2)

结果如下：

 data.frame(group,qd,g2)

   group class posterior.1  posterior.2 g2

1      1     2  0.47488392 5.251161e-01  2

2      1     1  0.97758726 2.241274e-02  1

3      1     1  0.91760361 8.239639e-02  1

4      1     1  0.89373652 1.062635e-01  1

5      1     1  0.99095426 9.045740e-03  1

6      1     1  0.80040675 1.995933e-01  1

7      1     1  0.95806785 4.193215e-02  1

8      1     1  0.99999650 3.504859e-06  1

9      1     1  0.68869999 3.113000e-01  1

10     1     1  0.52269207 4.773079e-01  1

11     2     2  0.22257679 7.774232e-01  2

12     2     2  0.14305840 8.569416e-01  2

13     2     2  0.01430849 9.856915e-01  2

14     2     2  0.26220789 7.377921e-01  2

15     2     1  0.75651148 2.434885e-01  1

16     2     1  0.56275471 4.372453e-01  1

17     2     2  0.03570597 9.642940e-01  2

18     2     2  0.01452116 9.854788e-01  2

19     2     2  0.07673785 9.232621e-01  2

20     2     2  0.05314826 9.468517e-01  2

(3).构建混淆矩阵

tab<-table(group,g2)

tab

结果如下：

tab<-table(group,g2)

> tab

     g2

group 1 2

    1 9 1

    2 2 8

tab<-table(group,g2)

> tab

     g2

group 1 2

    1 9 1

    2 2 8

tab<-table(group,g2)

> tab

     g2

group 1 2

    1 9 1

    2 2 8

sum(diag(prop.table(tab)))

[1] 0.85

6

(4).带入数据进行预测即可，不再重复了

以上介绍的是两个总体的距离判别，还有一类是多总体的距离判别。

还是再次po个案例。某地的市场上销售的电视机有多种品牌，然后随机抽取了20种牌子的电视机进行调查，质量评分q,功能评分f,销售价格p,销售状态是g3 。1代表畅销，2代表平销，3.代表滞销

数据如下：

q<-c(8.3,9.5,8.0,7.4,8.8,9.0,7.0,9.2,8.0,7.6,7.2,6.4,7.3,6.0,6.4,6.8,5.2,5.8,5.5,6.0)

f<-c(4.0,7.0,5.0,7.0,6.5,7.5,6.0,8.0,7.0,9.0,8.5,7.0,5.0,2.0,4.0,5.0,3.0,3.5,4.0,4.5)                                                                                                                                        

p<-c(29,68,39,50,55,58,75,82,67,90,86,53,48,20,39,48,29,32,34,36)

g3<-c(1,1,1,1,1,2,2,2,2,2,2,2,2,3,3,3,3,3,3,3)

plot(q,f)

text(q,f,g3,adj=-0.8,cex=0.75)

plot(q,p)

text(q,p,g3,adj=-0.8,cex=0.75)

plot(f,p)

text(c,p,g3,adj=-1,cex=0.75)

结果如下：

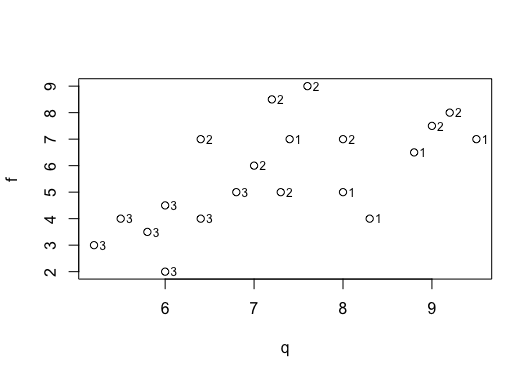
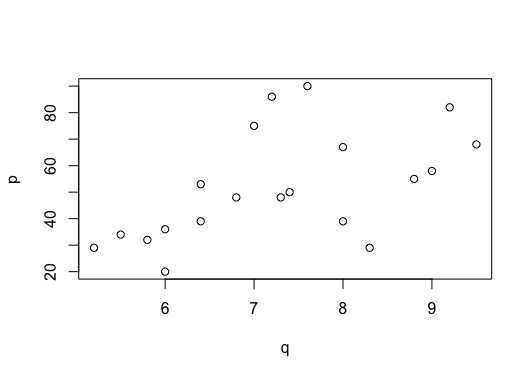    （2）线性判别（等方差 ）

ld3=lda(g3~q+f+p)

ld3

结果如下：

Call:

lda(g3 ~ q + f + p)

Prior probabilities of groups:

   1    2    3 

0.25 0.40 0.35 

Group means:

         q        f      p

1 8.400000 5.900000 48.200

2 7.712500 7.250000 69.875

3 5.957143 3.714286 34.000

Coefficients of linear discriminants:

          LD1         LD2

q -0.81173396  0.88406311

f -0.63090549  0.20134565

p  0.01579385 -0.08775636

Proportion of trace:

   LD1    LD2 

0.7403 0.2597 

进行分组判断和求解

代码如下：

lp3<-predict(ld3);lG3<-lp3$class

data.frame(g3,lG3)

ltab=table(g3,lG3)

ltab

diag(prop.table(ltab,1))

sum(diag(prop.table(ltab)))

结果如下：

> lp3<-predict(ld3);lG3<-lp3$class

> data.frame(g3,lG3)

   g3 lG3

1   1   1

2   1   1

3   1   1

4   1   1

5   1   1

6   2   1

7   2   2

8   2   2

9   2   2

10  2   2

11  2   2

12  2   2

13  2   3

14  3   3

15  3   3

16  3   3

17  3   3

18  3   3

19  3   3

20  3   3

> ltab=table(g3,lG3)

> ltab

   lG3

g3  1 2 3

  1 5 0 0

  2 1 6 1

  3 0 0 7

> diag(prop.table(ltab,1))

   1    2    3 

1.00 0.75 1.00 

> sum(diag(prop.table(ltab)))

[1] 0.9

（3）作图直观看一下：

plot(lp3$x);text(lp3$x[,1],lp3$x[,2],lG3,adj=-0.8,cex = 0.75)

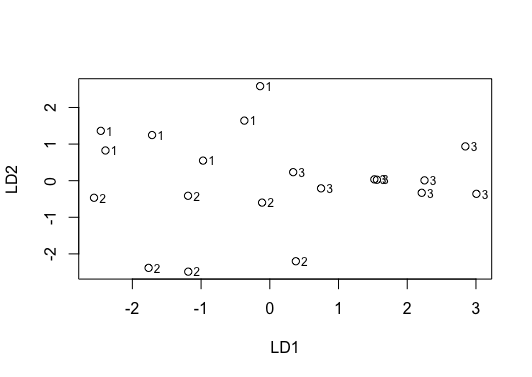
                                                                             随便写个数据进行待入，1畅销，2平销，3.滞销

predict(ld3,data.frame(q=7,f=9,p=70))

结果如下：

$class

[1] 2

Levels: 1 2 3

$posterior

           1         2            3

1 0.02668222 0.9725686 0.0007492256

$x

        LD1       LD2

1 -1.592724 -1.157613

说明该产品属于平销

我们在进行二次判别，当协方差阵不相同时，距离判别函数为非线性，方程较为复杂

qd3=qda(g3~q+f+p)

qd3

qp3=predict(qd3)

qG3=qp3$class

data.frame(g3,lG3,qG3)

qtab3=table(g3,qG3)

qtab3

sum(diag(prop.table(qtab3)))

predict(qd3,data.frame(q=7,f=9,p=70))

结果如下：

> qd3=qda(g3~q+f+p)

> qd3

Call:

qda(g3 ~ q + f + p)

Prior probabilities of groups:

   1    2    3 

0.25 0.40 0.35 

Group means:

         q        f      p

1 8.400000 5.900000 48.200

2 7.712500 7.250000 69.875

3 5.957143 3.714286 34.000

> qp3=predict(qd3)

> qG3=qp3$class

> data.frame(g3,lG3,qG3)

> qtab3=table(g3,qG3)

> qtab3

   qG3

g3  1 2 3

  1 5 0 0

  2 0 7 1

  3 0 0 7

> sum(diag(prop.table(qtab3)))

[1] 0.95

> predict(qd3,data.frame(q=7,f=9,p=70))

$class

[1] 2

Levels: 1 2 3

$posterior

            1         2            3

1 0.006317685 0.9936804 1.882737e-06

建立二次判别函数，带入预测数据，显示还是属于第二类

三.   Bayes判别准则

上面讲的几种判别方法，计算简单，结论明确，但是也是存在很多缺点：判别的方法与总体各自出现的概率大小完全无关；二是判别方法与错判后造成的损失无关，因此提出了一种新的判别方法。

Bayers 判别对多个总体的判别考虑的不只是建立判别式，而且还要计算新给样本属于各总体的条件概率p(j/x),j=1,2...k，比较这个k个概率的大小，然后将新样本判归为来自概率最大的总体。Bayers 判别准则是以个体归属于某类的概率（或某类判别函数值）最大或错判总体平均损失最小为标准。

(1)先验概率相等：q1=q2=q3=1/3,此时的判别函数类似于fisher线性判别函数

ld41<-lda(g3~q+f+p,prior=c(1,1,1)/3)

ld41

结果如下：

Call:

lda(g3 ~ q + f + p, prior = c(1, 1, 1)/3)

Prior probabilities of groups:

        1         2         3 

0.3333333 0.3333333 0.3333333 

Group means:

         q        f      p

1 8.400000 5.900000 48.200

2 7.712500 7.250000 69.875

3 5.957143 3.714286 34.000

Coefficients of linear discriminants:

          LD1         LD2

q -0.92307369  0.76708185

f -0.65222524  0.11482179

p  0.02743244 -0.08484154

Proportion of trace:

   LD1    LD2 

0.7259 0.2741 

（2）先验概率不等：取q1=5/20,q2=8/20,q3=7/20

ld42<-lda(g3~q+f+p,prior=c(5,8,7)/20)

ld42

z1<-predict(ld41)

z2<-predict(ld42)

data.frame(g3,ld41g<-z1$class,ld42g<-z2$class)

t1<-table(g3,z1$class)

sum(diag(t1))/sum(t1)

t2<-table(g3,z2$class)

sum(diag(t2))/sum(t2)

结果如下：

ld42<-lda(g3~q+f+p,prior=c(5,8,7)/20)

> ld42

Call:

lda(g3 ~ q + f + p, prior = c(5, 8, 7)/20)

Prior probabilities of groups:

   1    2    3 

0.25 0.40 0.35 

Group means:

         q        f      p

1 8.400000 5.900000 48.200

2 7.712500 7.250000 69.875

3 5.957143 3.714286 34.000

Coefficients of linear discriminants:

          LD1         LD2

q -0.81173396  0.88406311

f -0.63090549  0.20134565

p  0.01579385 -0.08775636

Proportion of trace:

   LD1    LD2 

0.7403 0.2597 

> z1<-predict(ld41)

> z2<-predict(ld42)

> data.frame(g3,ld41g<-z1$class,ld42g<-z2$class)

   g3 ld41g....z1.class ld42g....z2.class

1   1                 1                 1

2   1                 1                 1

3   1                 1                 1

4   1                 1                 1

5   1                 1                 1

6   2                 1                 1

7   2                 2                 2

8   2                 2                 2

9   2                 2                 2

10  2                 2                 2

11  2                 2                 2

12  2                 2                 2

13  2                 3                 3

14  3                 3                 3

15  3                 3                 3

16  3                 3                 3

17  3                 3                 3

18  3                 3                 3

19  3                 3                 3

20  3                 3                 3

> t1<-table(g3,z1$class)

> sum(diag(t1))/sum(t1)

[1] 0.9

> t2<-table(g3,z2$class)

> sum(diag(t2))/sum(t2)

[1] 0.9

（3）后验概率

round(z1$post*100,2)

round(z2$post*100,2)

predict(ld41,data.frame(q=7,f=9,p=70))

predict(ld42,data.frame(q=7,f=9,p=70))

结果如下：

 round(z1$post*100,2)

       1     2     3

1  98.26  0.56  1.19

2  79.42 20.57  0.01

3  93.72  4.31  1.97

4  65.37 33.71  0.91

5  90.52  9.44  0.05

6  92.78  7.21  0.00

7   0.33 86.32 13.34

8  17.75 82.25  0.01

9  18.47 81.05  0.48

10  0.28 99.70  0.02

11  0.22 99.69  0.09

12 11.12 77.98 10.90

13 29.18 32.50 38.32

14  0.08  0.02 99.90

15  1.21  2.27 96.52

16  7.94 24.27 67.79

17  0.01  0.04 99.95

18  0.14  0.28 99.58

19  0.10  0.43 99.47

20  1.38  2.52 96.10

> predict(ld41,data.frame(q=7,f=9,p=70))

$class

[1] 2

Levels: 1 2 3

$posterior

           1         2            3

1 0.04201444 0.9571429 0.0008426769

$x

        LD1       LD2

1 -1.344795 -1.523716

因此，这个预测数据代入预测的判别输入平销，并且概率为95.7%

predict(ld42,data.frame(q=7,f=9,p=70))

$class

[1] 2

Levels: 1 2 3

$posterior

           1         2            3

1 0.02668222 0.9725686 0.0007492256

$x

        LD1       LD2

1 -1.592724 -1.157613

同理，不想打字了。