之前分享过几篇关于电商多仓的派单流程-订单路由,其实里面还没有提及具体的派单算法实现,之前用的是贪心算法,把整单和拆单发货的场景都考虑进去了,相对比较智能一些,但也有缺点:如果像门店这样有几百家的数据时,效率就有点慢了。为此就有了今天的分享内容。
我们目前天猫的全渠道走的是天猫的前置派单功能,用的是天猫的逻辑,在订单下来的时候,订单里已经有门店的信息,然后把订单传到门店的收银系统里,目前用的是伯俊的云仓功能。提到伯俊系统,一言难尽。。。其他渠道计划用我们自己的派单功能,为订单寻仓,然后推送到伯俊系统。接下来就为大家介绍派单的核心逻辑。先介绍下处理的过程,把订单里需要发货的商品信息抽象成一个Map结构,Map<String,Integer>其中key为sku,value为qty,把所有门店的库存数据抽象为
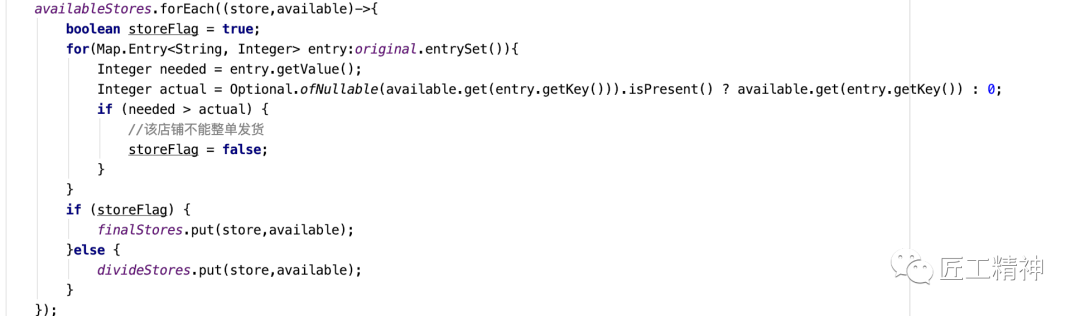
Map<String,Map<String,Integer>>其中key为门店的code,value为之前订单抽象的数据结构,有一点需要说明下,如果门店没有此款sku,qty设置为0,保证每家店的库存数据和订单数据是一致的。有了这样的数据结构,接下来分为两个步骤,其一是整单发货的情况,此种情况也很简单,伪代码如下:
availableStores.forEach((store,available)->{
boolean storeFlag = true;
for(Map.Entry<String, Integer> entry:original.entrySet()){
Integer needed = entry.getValue();
Integer actual = Optional.ofNullable(available.get(entry.getKey())).isPresent() ? available.get(entry.getKey()) : 0;
if (needed > actual) {
//该店铺不能整单发货
storeFlag = false;
}
}
if (storeFlag) {
finalStores.put(store,available);
}else {
divideStores.put(store,available);
}
});
其二就是拆单发货的情况,相对比较复杂些,这里主要介绍一种思想吧,有兴趣的可以尝试下,我们这样来思考问题,订单里需要的sku及其qty是固定的,门店及其相应的sku和qty是一个集合,我们抽象成这样一个问题:给定一个数组,求解数组里的任意组合数之和大于等于某个常量。这个数组就是我们门店对应的商品库存,形式为[qty1,qty2,qty3,...qtyn],常量就是订单里sku的数量。对于一单一件的已经结束了,多件的情况下,需要多次运用该算法,然后在集合里再求解。核心逻辑如下:
/**
* @author villiam.li
* @date 2021-10-02
*
* 回溯法求解最小组合
*
* 背景需求:当所有店铺不能满足整单发货时,需要考虑门店拆单发货的情况,
* 一个订单里的需要的sku及其数量是固定的,如何在所有门店可用的库存集合里找出最优解。抽象为这样一种算法实现:
* ************** 求解一个集合里用最少的组合来满足固定和的问题。************************
* 接下来就是算法的实现了:
* 开辟一个与original相同长度的数组(originalBin)。这个数组里面都是二进制。假设original的长度,originalBin长度为3
* 将original从 000 001 010 011 100 101 110 111 只要末尾不断加1并且不超过2
* 然后将original的相应位置与originalBin的相应位置的数据相乘
* 若original数据为[ 1, 2, 3 ];min = 2; max =4; count = 2
* originalBin 可能值为:[0,0,0] [0,0,1] [0,1,0] [0,1,1] [1,0,0] [1,0,1] [1,1,0] [1,1,1]
* sum 0 1*3 1*2 1*2+1*3 1*1 1*1+1*3 1*1+1*2 1*1+1*2+1*3
* 只要sum>=min&&sum<=max至于count只要在符合sum的前提下originalBin的1的个数<=count就行
*/
public class Backtracking {
/**
* 原始数组,此处为每个店铺相应sku的库存数
*/
private Integer[] original;
/**
* 二进制数组,数组长度大小和 original 一样
*/
private Integer[] originalBin;
/**
* 最小值,实际场景总min和max相等
*/
private Integer min = 1;
/**
* 最大值,实际场景总min和max相等
*/
private Integer max = 2;
/**
* 组合数量,默认值为2
*/
private Integer count = 2;
/**
* 构造函数,初始化数据
* @param original
* @param min
* @param max
* @param count
*/
public Backtracking(Integer[] original, Integer min, Integer max, Integer count){
this.original = original;
this.originalBin = new Integer[original.length];
this.min = min;
this.max = max;
this.count = count;
}
/**
* 获取总的集合
* @return
*/
public List<List<Integer>> buildResult(){
List<Integer> result;
List<List<Integer>> list = new ArrayList<>();
double b = (double)this.original.length;
int loopCount = (int)Math.pow(2.0, b)-1;
int index = 0;
while(index < loopCount){
index += 1;
result = get(index,this.min,this.max,this.count);
if(CollectionUtils.isNotEmpty(result)){
list.add(result);
}
}
return list;
}
/**
* 依此递增,计算满足的集合
* @param parseInt
* @param min
* @param max
* @param count
* @return
*/
private List<Integer> get(int parseInt,Integer min, Integer max,Integer count) {
List<Integer> result = new ArrayList<>();
int sum = 0;
int j = 0;
int y = 0;
int p;
Arrays.fill(originalBin, 0);
if(y > count){
return Collections.emptyList();
}
while(parseInt>0){
p = parseInt % 2;
parseInt = parseInt 2;
if(p == 1){
y++;
result.add(original.length-1-j);
}
originalBin[j++] = p;
}
for(int i = originalBin.length-1; i>=0; i--) {
sum += original[original.length-1-i] * originalBin[i];
}
if(sum >= min && sum <=max){
return result;
}
return Collections.emptyList();
}
}
以上是算法的一种实现方式,此处也抛一个问题给大家,此种算法也有瓶颈~可以尝试下。期待有更优的算法来实现。
总结
今天也抛砖引玉一下,期待有更好的实现。始终相信那句话:大道至简。任何事情都一样,越复杂的事情越可以分解成简单的可处理的步骤。也经常跟小伙伴们说,想法很重要,作为程序员的我们应该体会更深,在你实现一个需求功能时,我相信思考的时间远大于coding的时间。期待有缘人的高见~






