OpenGL绘制贝赛尔曲线

周末随心分享 2021-05-09

880

背景

贝塞尔曲线(Bézier curve)，又称贝兹曲线或贝济埃曲线，是应用于二维图形应用程序的数学曲线。一般的矢量图形软件通过它来精确画出曲线。

利用贝塞尔曲线，我们可以更平滑的画出手势操作的轨迹，然后实现像橡皮檫等功能，n阶贝兹曲线可如下推断。给定点P0、P1、…、Pn，其贝兹曲线即：

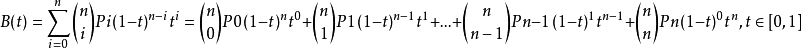
t 值的计算方式为：j/N，N代表要生成的贝塞尔点个数，n代表控制点的数量，通常我们可以取三个控制点，即n=2, 此时第j个贝塞尔点坐标为 B(t) = (1-t)^2*P0 + 2*(1-t)*t*P1 + t^2*P2 （j范围是[0, N)）

实现

知道了贝塞尔曲线的公式后我们如何绘制一条圆滑的曲线呢，这里又分成两种情况，如果一开始就知道所有的控制点，那么直接代入公式就能实现曲线绘制，但是像手势操作这种是随着手指移动而收集控制点的情况，只能绘制部分曲线，然后两条曲线之间取重叠区域点作为控制点来达到一定过渡，当然这种情况下的曲线衔接处会有点瑕疵，不过针对橡皮擦这种要求没那么严格的也足够了~

下面来看一下具体步骤：

1、 注册手势监听

@Override
public boolean onTouchEvent(final MotionEvent event) {
     if (event != null) {
         int action = event.getAction() & MotionEvent.ACTION_MASK;
         final float x, y;
         switch (action) {
             case MotionEvent.ACTION_DOWN:


                 handleActionDown(event);


                 break;
             case MotionEvent.ACTION_POINTER_DOWN:


                 break;
             case MotionEvent.ACTION_MOVE:
                   handleActionMove(event);
                 break;
            case MotionEvent.ACTION_POINTER_UP:
                 break;
            case MotionEvent.ACTION_UP:


                 break;
         }
         return true;
     }
     return false;
}

2、处理ACTION_DOWN和ACTION_MOVE传过来的手势点：

void handleActionDown(MotionEvent event) {
     scrawlDownX = event.getX();
     scrawlDownY = event.getY();


     points.clear();
     //转换成OpenGL坐标系中的坐标
     PointF point = translateToGL(event.getX(), event.getY());
     addBezierPoint(point);
}


void handleActionMove(MotionEvent event) {
    if (Math.abs(scrawlDownX - event.getX()) > VALID_SPACING
             || Math.abs(scrawlDownY - event.getY()) > VALID_SPACING) {
       PointF point = translateToGL(event.getX(), event.getY());
       if (bindFBO(mMaterialMaskTexture)) {
           addBezierPoint(point);
           unBindFBO();
       }
    } 
}

上面我们会根据每次传过来的点生成一个新的贝塞尔曲线点，然后将轨迹写入到蒙层里面，接下来看看怎样生成贝塞尔曲线点：

private void addBezierPoint(PointF point) {
    if (points.size() == 3) {
        points.remove(0);
    }
    points.add(point);


    if (points.size() == 2) {
        PointF from = points.get(0);
        PointF to = midPoint(points.get(0), points.get(1));
        PointF control = midPoint(from, to);


        calculateBezierCurve(from, to, control);
    } else if (points.size() > 2) {
        PointF from = midPoint(points.get(0), points.get(1));
        PointF to = midPoint(points.get(1), points.get(2));
        PointF control = points.get(1);


        calculateBezierCurve(from, to, control);
    }
}


private PointF midPoint(PointF p1, PointF p2) {
    return new PointF((p1.x + p2.x)  2, (p1.y + p2.y)  2);
}


/**
 * 涂抹贝塞尔曲线两点之间插入的点数量，影响涂抹程度值
 */
private static final int BEZIER_INSET_POINT = 5;
/**
 * 默认笔触大小
 */
private static final float DEFAULT_PEN_SIZE_RATIO = 20  750f;


/**
 * 羽化的涂抹笔触，会比实际看过去的笔触小，所以此处需要有一个比例，使看过去涂抹的范围与笔触圆圈接近
*/
private static final float MASK_SCALE = 5  4f;


/**
 * 笔触大小，比例值
 */
private float mPenSize = DEFAULT_PEN_SIZE_RATIO * 2 * MASK_SCALE;
/**
 * 涂抹正方形区域比例
 */
private float mEraserRatio = mPenSize;


private void calculateBezierCurve(PointF from, PointF to, PointF control) {
    int xNum = (int) ((to.x - from.x)  mEraserRatio * BEZIER_INSET_POINT);
    int yNum = (int) ((to.y - from.y)  mEraserRatio * mHeight  mWidth * BEZIER_INSET_POINT);


    // 坐标点的总数
    int N = Math.max(Math.abs(xNum), Math.abs(yNum));
    N = Math.max(N, 1);


    final float[] array = new float[8 * N * 2];


    float x, y, t;
    for (int i = 0; i < N; i++) {
        t = (float) i  N;


        // 根据贝塞尔曲线函数，获得此时的x,y坐标
        x = (1 - t) * (1 - t) * from.x + 2 * (1 - t) * t * control.x + t * t * to.x;
        y = (1 - t) * (1 - t) * from.y + 2 * (1 - t) * t * control.y + t * t * to.y;


        addVertex2Array(array, x, y, 16 * i);
    }


    // 一个点相当于一个矩形，一个矩形画两个三角形，使用6个索引
    final short[] indexArray = new short[N * 6];
    for (int i = 0; i < N; i++) {
        //leftBottom,rightBottom,leftTop
        indexArray[i * 6] = (short) (4 * i);
        indexArray[i * 6 + 1] = (short) (4 * i + 1);
        indexArray[i * 6 + 2] = (short) (4 * i + 2);


        //rightBottom,rightTop,leftTop
        indexArray[i * 6 + 3] = (short) (4 * i + 1);
        indexArray[i * 6 + 4] = (short) (4 * i + 3);
        indexArray[i * 6 + 5] = (short) (4 * i + 2);
    }


    mEraserFilter.initVertexData(array);
    mEraserFilter.setIndexData(indexArray);
    glViewport(0, 0, mWidth, mHeight);
    mEraserFilter.drawElements(mMaskTexture);
    unBindFBO();
}


 /**
 *这边点的坐标y值直接考虑了渲染翻转，所以会取相反数
 */
private void addVertex2Array(float[] vertexArray, float x, float y, int index) {
    //leftBottom顶点坐标
    vertexArray[index] = x - mEraserRatio;
    vertexArray[index + 1] = -(y - mEraserRatio * mWidth / mHeight);
    //leftBottom纹理坐标
    vertexArray[index + 2] = 0f;
    vertexArray[index + 3] = 1f;
    //rightBottom顶点坐标
    vertexArray[index + 4] = x + mEraserRatio;
    vertexArray[index + 5] = -(y - mEraserRatio * mWidth / mHeight);
    //rightBottom纹理坐标
    vertexArray[index + 6] = 1f;
    vertexArray[index + 7] = 1f;
    //leftTop顶点坐标
    vertexArray[index + 8] = x - mEraserRatio;
    vertexArray[index + 9] = -(y + mEraserRatio * mWidth / mHeight);
    //leftTop纹理坐标
    vertexArray[index + 10] = 0f;
    vertexArray[index + 11] = 0f;
    //rightTop顶点坐标
    vertexArray[index + 12] = x + mEraserRatio;
    vertexArray[index + 13] = -(y + mEraserRatio * mWidth / mHeight);
    //rightTop纹理坐标
    vertexArray[index + 14] = 1f;
    vertexArray[index + 15] = 0f;
}

过程大概是：

每次选取三个点作为贝塞尔曲线公式里面的控制点来画曲线段，即起点、中点、目标点，为了使轨迹更平滑，起点的选择有两种情况，如果只有两个点，那么就选前一个点，如果超过了两个点，会选择前两个点的中点；然后目标点就是当前点和前一个点的中点，最后中点就是起点和目标点间的中间点或者平均值
将选择的三个点作为三阶公式的控制点传给贝塞尔曲线公式，计算得出贝塞尔点
为了使点更密集（曲线边缘更圆滑），可以在起点和终点间插入一定量的贝塞尔点，即公式中N的定义
生成的贝塞尔点转换成openGL坐标，每个点位置处画矩形，因为点生成的速度和量都非常多，所以这边用到了drawElements这种快速绘制的函数，具体使用可以参考网上的样例
经过上面操作就能将当前手势操作的轨迹画到蒙层里面，相当于保存了轨迹，然后想恢复的话可以用同样的操作擦除蒙层的轨迹，最终将蒙层映射到原图里面就实现了擦除和恢复功能
注意写入FBO时是上下颠倒的，所以计算坐标时将y轴的值颠倒过来，实现绕x轴翻转的功能，当然也可以利用矩阵来实现翻转，上面代码就直接对坐标处理了

3、羽化

经过上面的处理可以看到手势的轨迹了，但是这还没结束，你会发现轨迹有严重的锯齿现象，原因是什么呢？就是因为我们用OpenGL画的是矩形，所以改善的方法就是要画圆形

那怎么画圆形呢，肯定不是用openGL渲染出来的，那样不仅效率低，而且不是我们要的效果，我们需要一张mask图，这张图从中心到四周，不透明度从大到小逐渐过渡，类似下面这张图：

有了遮罩，我们就可以把这张图的RGB里面的r值作为透明度，下面具体看一下实现：

1）修改橡皮檫对应的脚本：

precision highp float;
varying vec2 texcoordOut;
uniform sampler2D masktexture;
uniform float opacity;
 
void main() {
     vec4 maskColor = vec4(1.0, 0.0, 0.0, 1.0);
     vec4 textureColor = texture2D(masktexture,texcoordOut);
     gl_FragColor = maskColor * textureColor.r * opacity;
}

上面的masktexture就是我们需要的那张圆形图，opacity变量的作用是调整橡皮檫渐变擦除功能，即你要多少步内把擦除部分全部擦除，然后可以看到我们画上去的颜色选的是masktexture的r值

2）设置叠加方式，即选择擦除还是恢复：

if (mMode == MODE_ERASER) {
    glBlendEquation(GL_FUNC_ADD);
    glBlendFunc(GL_ONE, GL_ONE);
} else if (mMode == MODE_RECOVER) {
    glBlendEquation(GL_FUNC_REVERSE_SUBTRACT);
    glBlendFunc(GL_ONE, GL_ONE);
}

这边就用到了OpenGL提供的图像混合方式了，因为我们每次画上去的时候无法拿到当前FBO里面的数据（ios有扩展可以），所以我们需要用这种方式来将当前FBO里面的数据和我们即将画上去的数据做叠加（如果不考虑FBO里面数据，会导致画上去的颜色影响之前的轨迹），这边考虑了两种模式：

如果是橡皮檫模式，我们的公式会变成
resultColor = srcColor * 1 + dstColor * 1;
其中srcColor就是masktexture里面的r值，因为这个r值是由中心到四周过渡的，所以每次画上去的就相当于一个羽化过的圆
如果是恢复模式，我们的公式变成：
resultColor = dstColor *1 – srcColor * 1;
即把我们橡皮檫模式下画上去的颜色消除，这样轨迹就相当于被擦除了
利用上面两步操作后我们会生成一张橡皮檫轨迹的纹理，其中纹理上面的r值代表轨迹的透明度，然后我们将轨迹的纹理和素材原图的纹理做混合，混合结果中素材的透明度就取决于轨迹的r值。
如果要设置多少步内擦除，可以设置变量：
opacity = 1.0f / BEZIER_INSET_POINT / mScrawlCount;
其中mScrawlCount就代表完全擦除的步数，而之所以要除以BEZIER_INSERT_POINT是因为在每次滑动过程中为了边缘更加圆滑我们会插入一些贝塞尔点进行重叠绘制，类似下面这张图，橙色圆被多个蓝色圆重叠

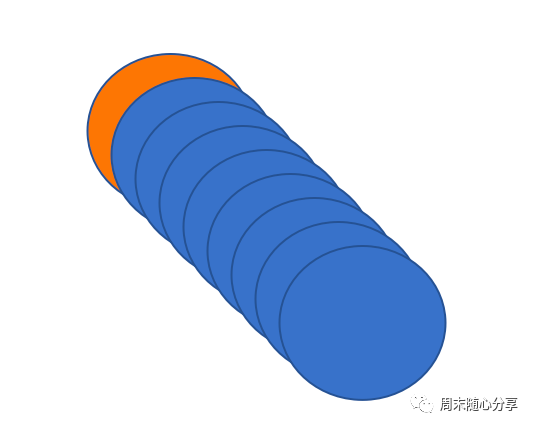
而这些蓝色圆每次绘制就会在橙色圆上执行一次masktexture的绘制，这样相当于橙色圆擦除了多次，所以需要消除这个影响

总结

OpenGL虽然只能绘制点、线、三角形，但是任何一种图形都可以由这三种基本形状组合而成，比如圆就可以分割成多个小三角形。因此OpenGL才能渲染出像游戏里那种丰富的场景，感兴趣的小伙伴也可以动手试试，绘制一条自己的曲线看看^_^

好了，今天周末君的分享就到这了，下周会继续介绍OpenGL相关特性，毕竟它的魅力可不止目前提到的这些！

数据库

文章转载自周末随心分享，如果涉嫌侵权，请发送邮件至：contact@modb.pro进行举报，并提供相关证据，一经查实，墨天轮将立刻删除相关内容。

OpenGL绘制贝赛尔曲线

评论