背景
上周周末君给大家初步介绍了OpenGL是如何绘制一个矩形的过程,但是我们生活中更常见的是游戏里的场景,比如和平精英里人物是怎么移动的,视角是怎么变换的,以及仿真的3D建模是怎样实现的,这一切的一切说到根源离不开今天要介绍的内容——坐标系&矩阵变换
坐标系
正如我们所存在的世界一样,要构建一个游戏场景,必须基于一定坐标系进行构建,现实生活目前发现的最高级别纬度就是三维坐标系了,当然还可能有四维(时间坐标系)、五维等等...好了,扯远了,我们先来看看OpenGL坐标系是怎样的吧
OpenGL总共有三种坐标系,分别是右手坐标系、NDC坐标系、屏幕坐标系,我们传入的顶点坐标会经过这三种坐标系的逐一转换,最终绘制到屏幕,分别介绍一下这三种坐标系:
OpenGL坐标系(右手坐标系)
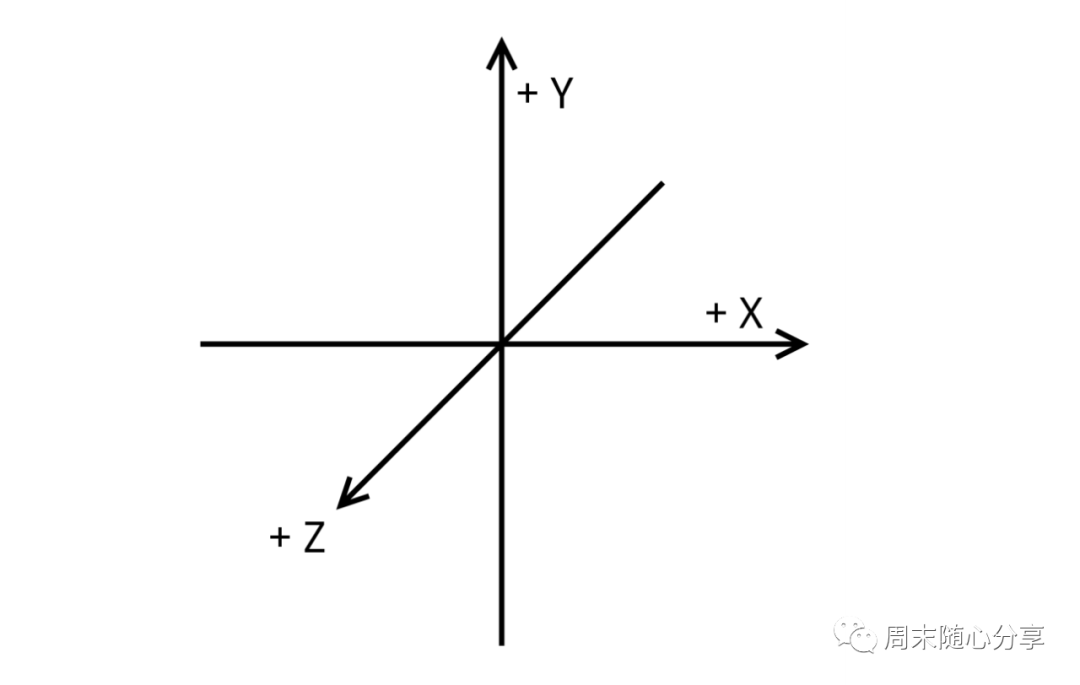
右手坐标系顾名思义,就是举起你的右手,掌心向上,食指水平向前,中指垂直向脸,拇指水平向右,这个坐标系就是我们代码面向的坐标系,还记得我们上周介绍的顶点坐标吗,就是根据这个坐标系来取点
坐标系中心点就是屏幕中心点,所以根据你在屏幕的位置可以取对应的值构建物体的顶点坐标
NDC坐标系(左手坐标系)
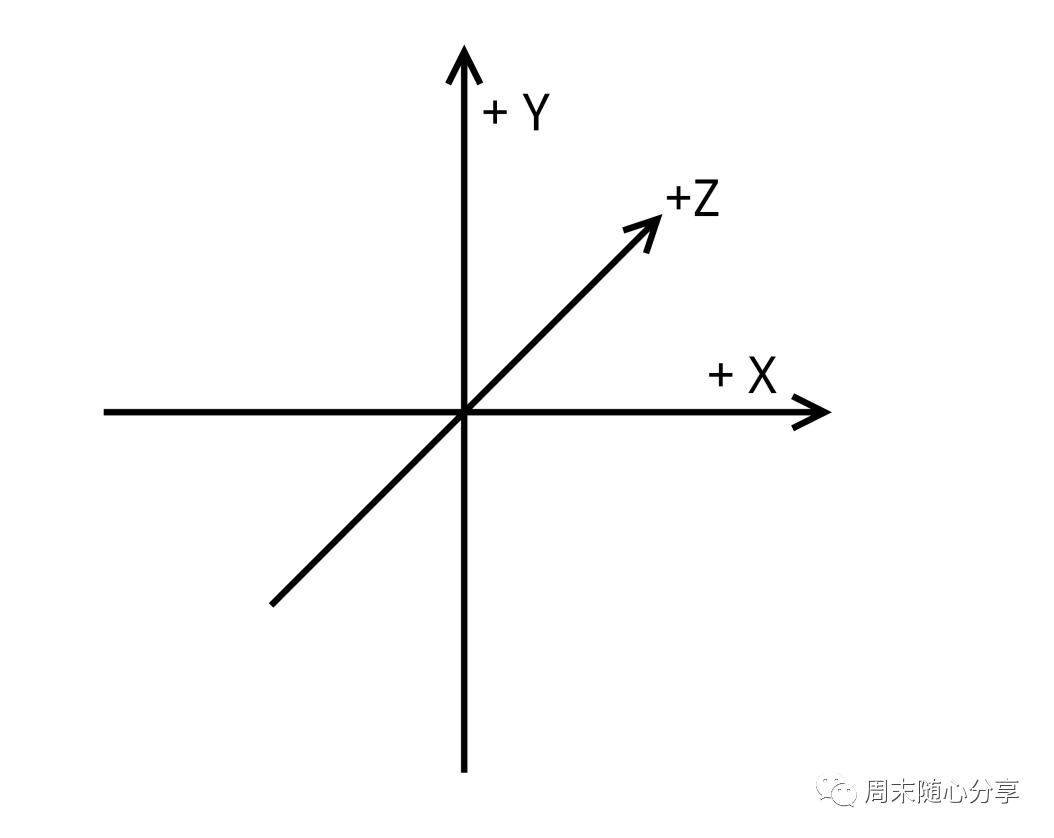
和右手坐标系类似,左手坐标系换成举起你的左手而已,但是掌心向下,所以区别就是z轴方向相反,除了z轴不一样,NDC坐标系也叫裁剪坐标系,会把范围在【-1,1】之外的视野全部裁掉,所以当你发现看不到你要渲染的物体时可以看看是不是顶点坐标在这范围之外了
当我们把定义后的顶点坐标传到OpenGL进行渲染时,坐标会经历下面变换:[x, y, z, w] = [x/w, y/w, z/w, 1],所以这里w变量作用就是进行范围约束,下面我们还会提到
屏幕坐标系

屏幕坐标系比较好理解,就是以手机屏幕左上角为准,向右向下扩展,和我们肉眼见到的比较贴合,这里就不多介绍了
矩阵变换
有了坐标系我们就可以确定物体的位置,但是一个生动活泼的物体是会平移旋转缩放,同时为了更符合人眼视角,还会有一定的投影变换,这就涉及接下来要介绍的矩阵变换了
OpenGL矩阵变换主要有三种,分别是Model、View、Projection,一个二维平面坐标经过这三种矩阵处理后就能变成肉眼熟悉的场景了,下面分别介绍一下这三种变换:
Projection
正交投影(Orthographic),也叫平行投影,如下图,平行投影看到场景不会根据视野范围进行变换,即看到完整的立方体内容
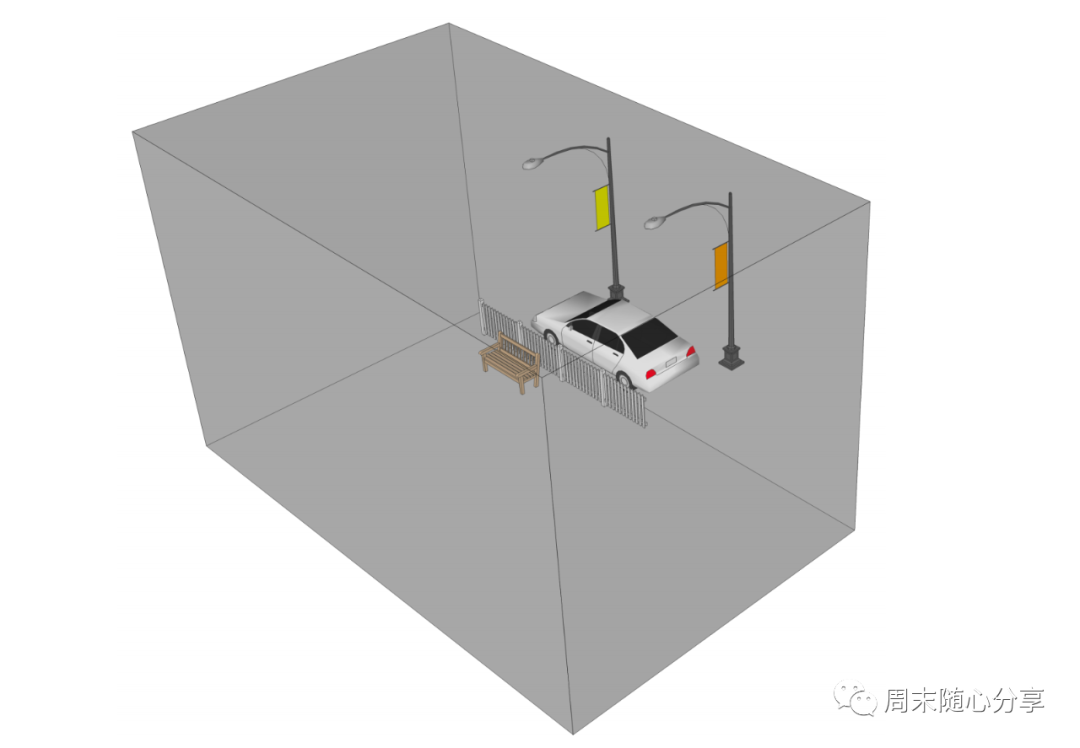
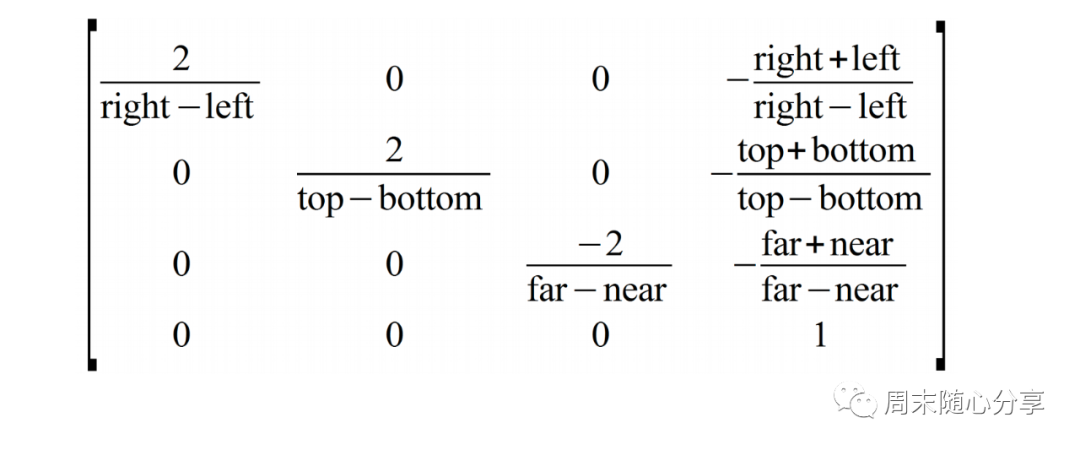
透视投影(Perspective),也叫中心投影,同样来看一下图,如下,我们看到的范围会模拟人的视野范围,越远的物体看起来越小,越近的看起来越大,视野呈现三角锥范围
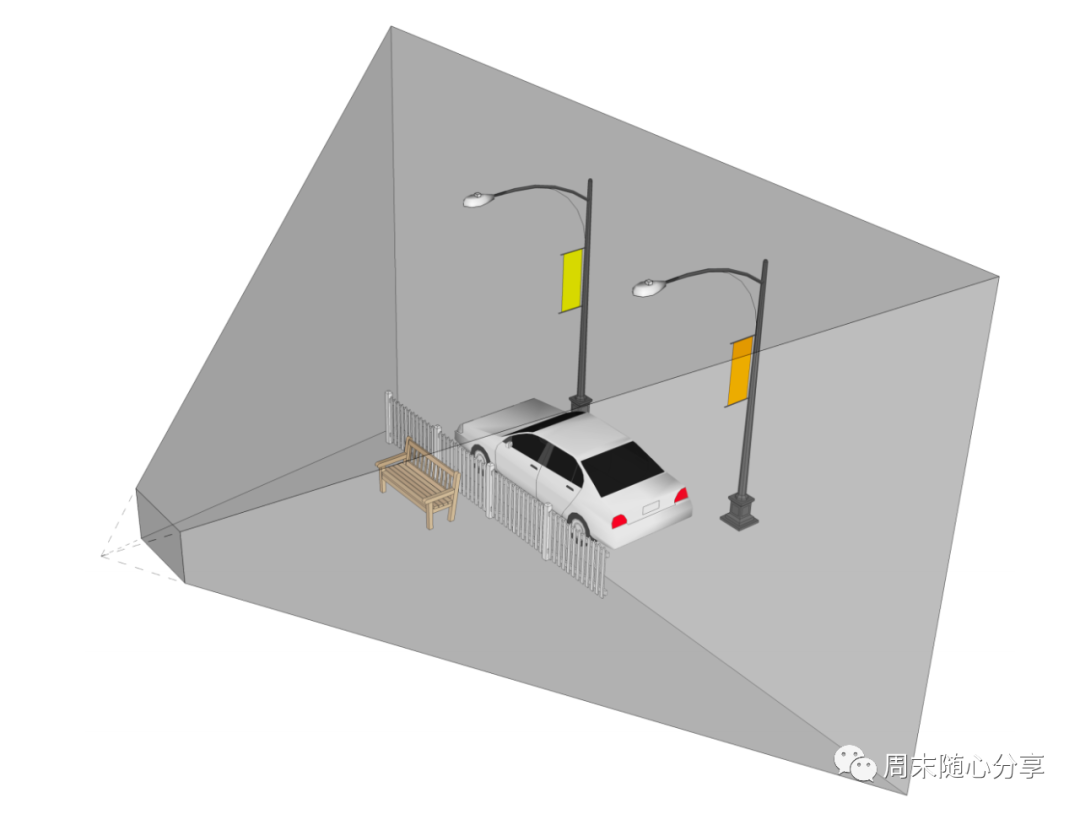
同样先来看一下它的矩阵变换:

根据公式可以看出,透视投影根据z轴大小作为w分量,而w又会影响x、y的大小,从而达到了根据由近到远调整物体位置大小的幅度不一样,形成透视效果
View
上面提到的投影变换影响的是大小,但是观察的点不会变,即你看到的角度是一定的,所以我们还需要一个角度的变换,角度变换可以理解为眼睛的位置以及目光的方向
视角变换会影响全部对象,当然可以给每个对象添加一样的Model矩阵也能达到同样效果,但是把这种全局操作放在一个单独矩阵会更加简洁,下面的图就比较形象的表达出这种变换原理:
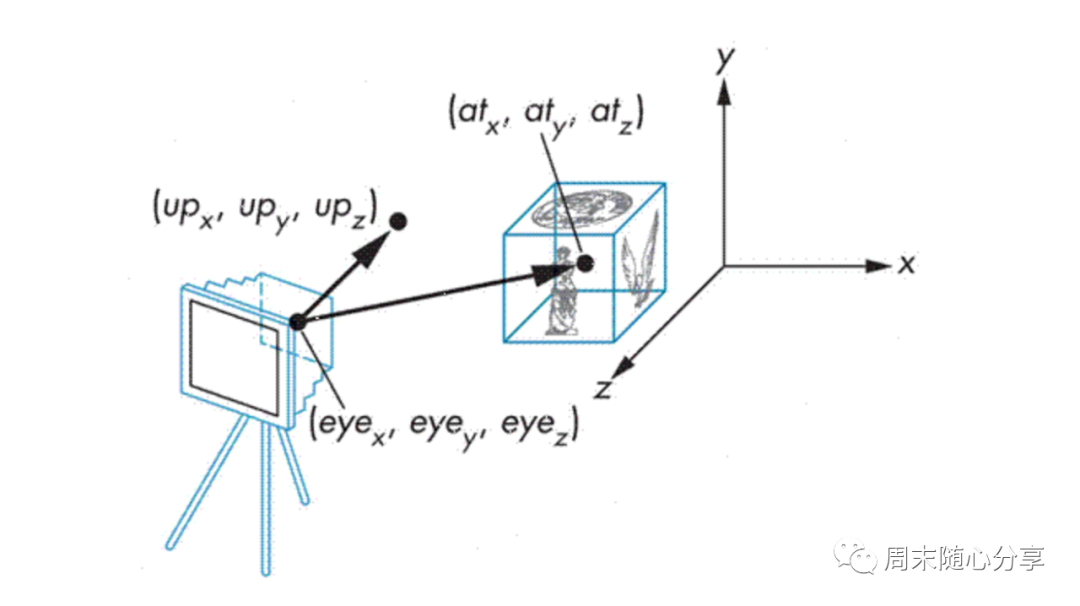

Model
经过上面两种变换,我们看到的物体已经接近现实生活中看到的真实物体了,但是正如一开始提到的,物体是要动的,总不能让我们一直盯着它不动吧,那样多无聊,因此来到了我们最后一个变换——模型变换

模型变换主要包括以下三种
旋转:OpenGL中旋转是围绕坐标系中心点旋转,所以旋转前需要先把物体挪到中心位置
平移:平移可以朝着x、y、z三个方向移动,只是大小要安装坐标系大小来计算
缩放:缩放同样可以进行三维方向缩放,大小也是按照坐标系大小
总结
经过上面介绍,小伙伴们应该对OpenGL如何绘制一个物体有了更深的了解吧,可以想想和平精英里看到的场景再结合这边说的,是不是对游戏里的场景没那么神秘了,下次大家也可以自己动手写个小游戏试试O(∩_∩)O哈哈~
好了,今天周末君的分享就到这了,下周我们继续介绍更多OpenGL特性~






