最优二叉树的基础知识是软件评测师考试的重要考点，经常出现在上午场的客观选择题当中。1951年，哈夫曼在麻省理工学院攻读博士学位，他和修读信息论课程的同学的选择是完成学期报告还是期末考试。导师出的学期报告题目是：查找最有效的二进制编码。由于无法证明哪个已有编码是最有效的，哈夫曼放弃对已有编码的研究，转向新的探索，最终发现了基于有序频率二叉树编码的想法，并很快证明了这个方法是最有效的，也就是后来以他名字命名的哈夫曼编码。下面就该知识点并结合例题进行总结学习。
一、最优二叉树概述
最优二叉树又称为哈夫曼树或霍夫曼树，是一类带权路径长度最短的树。路径是从树中一个结点到另一个结点之间的通路，该通路上分支数目称为路径长度。树的路径长度是从树根到每一个叶子之间的路径长度之和。结点的带权路径长度为从该结点到树根之间的路径长度与该结点权值的乘积。
树的带权路径长度WPL为树中所有叶子结点的带权路径长度之和，记为：
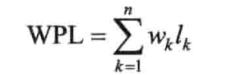
其中，n为带权叶子结点数目，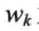
为叶子结点的权值，
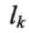为叶子结点到根的路径长度。
最优二叉树是指权值为w1，w2, ...，wn的n个叶子结点的二叉树中带权路径长度最小的二叉树。例如，在下图所示的具有4个叶子结点的二叉树中，图(b)所示二叉树的带权路径长度最小。
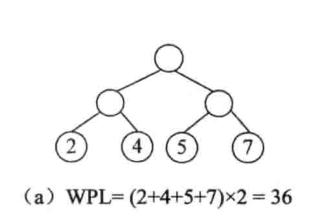
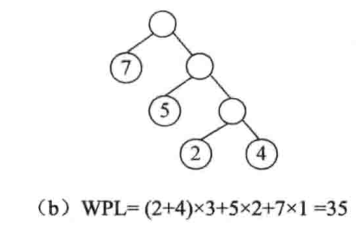
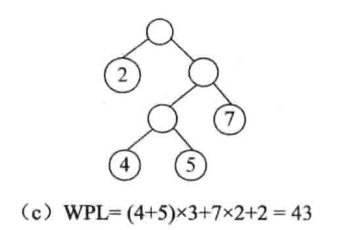
二、构造最优二叉树的过程
（1）根据给定的n个权值{w1, w2, …，wn}， 构成n棵二叉树的集合F= {T1, T2, …Tn}，其中，每棵树Ti中只有一个带权为wi的根结点，其左、右子树均空。
（2）在F中选取两棵权值最小的树作为左、右子树构造一棵新的二叉树，新构造二叉树的根结点的权值为其左、右子树根结点的权值之和。
（3）从F中删除这两棵树，同时将新得到的二叉树加入到F中。
（4）重复（2）、（3）步，直到F中只含一棵树时为止，这棵树便是最优二叉树(哈夫曼树)。
三、哈夫曼编码
若对每个字符编制相同长度的二进制码，则称为等长编码。例如，英文字符集中的26个字符可采用5位二进制位串表示，（很多学员可能会问为什么要用5位二进制表示？因为4位二进制的话，只能表示2的4次方，也就是16个字符，而2的5次方可以表示32个字符），按等长编码格式构造一个字符编码表。发送方按照编码表对信息原文进行编码后送出电文，接收方对接收到的二进制代码按每5位一组进行分割，通过查字符的编码表即可得到对应字符，实现译码。
如果要设计长度不等的编码，必须满足下面的条件：
任一字符的编码都不是另一个字符的编码的前缀，这种编码也称为前缀码。对给定的字符集D={d1，d2，…，dn}及字符的使用频率W={w1，w2，…，wn}，构造其最优前缀码的方法为：以d1，d2，…，dn作为叶子结点，w1，w2，…，wn作为叶子结点的权值，构造出一棵最优二叉树，然后将树中每个结点的左分支标上0，右分支标上1，考试的时候目前默认权值小的作为左孩子，权值稍大的作为右孩子。则每个叶子结点代表的字符的编码就是从根到叶子的路径上的0、1组成的串。
下面是近几年对该知识点考察过的真题，以后仍是考试出题的重点，大家要重视起来。
【2019年第45-46题】己知某文档仅包含6种不同的字符，其每个字符出现的频率如下表所示，采用霍夫曼编码对该文档压缩存储，则单词“face”的编码为(1)，该文档的压缩比为(2)。
（1）
A、110001001101
B、101000010100
C、001101001100
D、110101001100
（2）
A、20%
B、25%
C、30%
D、40%
解析：本题考查程序设计语言中二叉树数据结构的基础知识。
按照上面知识点所讲的构造方法：
（1）先找到权值最小的节点f、e，构造成一个权值为14的新节点，放到原来的表中，删除f、e这两个用过的节点。
（2）然后继续寻找剩下节点中权值最小的两个，发现是c和b，继续构造成权值为25的新节点，放到原来的表中，删除c、b这两个用过的节点。
（3）然后继续寻找剩下节点中权值最小的两个，发现是14和d，继续构造成权值为30的新节点，放到原来的表中，删除14、d这两个用过的节点。
（4）然后继续寻找剩下节点中权值最小的两个，发现是25和30，继续构造成权值为55的新节点，放到原来的表中，删除25、30这两个用过的节点。
（5）然后继续寻找剩下节点中权值最小的两个，发现就剩下了a和55，继续构造成权值为100的新节点至此构造完毕。构造霍夫曼树如下图所示：
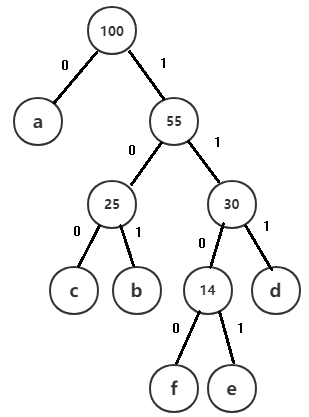
由图可得各个字符的编码如下：
a：0；
b：101；
c：100；
d：111；
e：1101 ；
f：1100；
所以face的编码为：1100 0100 1101。
压缩前，属于等长编码，每个字符用3位编码足够表示，因为2位二进制只能表示2的2次方，也就是4个字符，3位二进制能表示8个字符，所以浪费了，所以采用霍夫曼编码可以压缩编码长度。压缩后编码长度为：1*45%+3*13%+3*12%+3*16%+4*9%+4*5%=2.24；
压缩率为：（3-2.24）/3≈25%；
故正确答案为：（1）A （2）B
作者唯一官方个人微信公众号（昊洋与你一起成长）：HYJY20180101
写于2021年10月15日
作者：昊洋讲师
版权所有，侵权必究
