• 参考

• 正文

• cbc

• Padding Oracle Attack

参考

http://blog.zhaojie.me/2010/10/padding-oracle-attack-in-detail.html
https://skysec.top/2017/12/13/padding-oracle和cbc翻转攻击/
https://www.freebuf.com/articles/database/151167.html

正文

今天团队里的师傅分享了一道题目涉及到了
cbc中的padding Oracle attack
简单的cbc原先研究过 也做过类似的题目
像实验吧中的简单的登陆题
http://ctf5.shiyanbar.com/web/jiandan/index.php
这里不做过多叙述

cbc

先放两张图
一图胜万字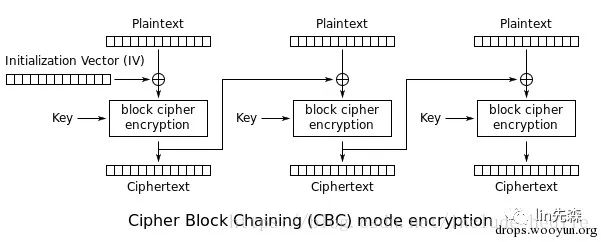


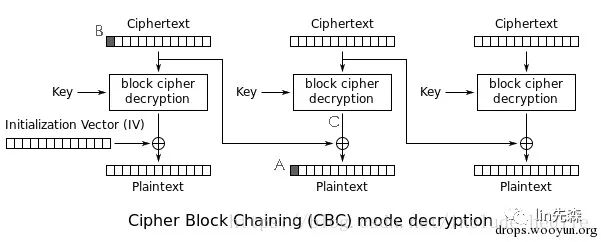
分别描述了cbc模式的加密 和 解密 两个过程

CBC是一种加密的模式，经常把DES或者AES算法（两种分组密码算法）作为加密使用的算法。
对于采用DES算法进行加密的内容，填充规则遵循的是PKCS #5，而AES则是PKCS #7，实际上两者的要求基本一样，区别在于PKCS #5填充是八字节分组而PKCS #7是十六字节

Padding Oracle Attack

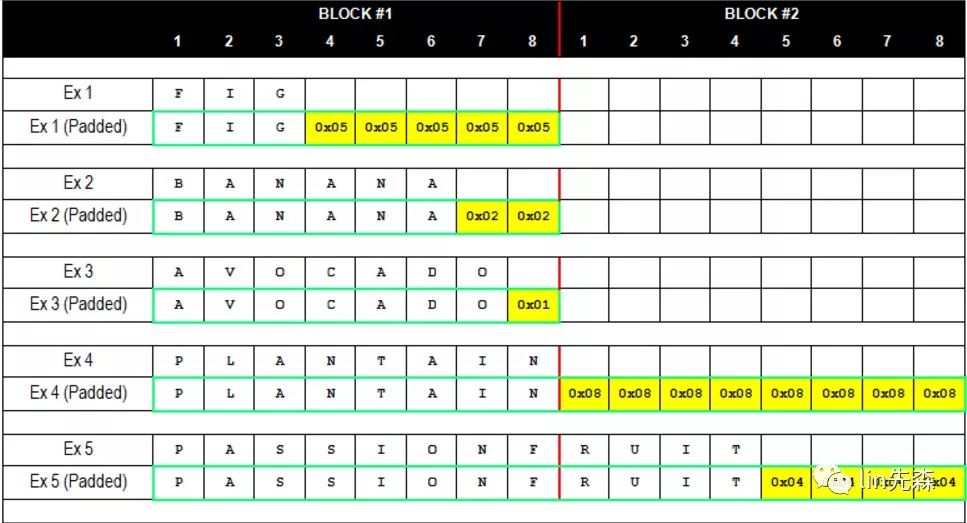
PKCS #7
比如我们的明文为admin
则需要被填充为 admin\x0b\x0b\x0b\x0b\x0b\x0b\x0b\x0b\x0b\x0b\x0b

一共11个\x0b

Padding Oracle Attack是针对CBC链接模式的攻击，和具体的加密算法无关，换句话说，这种攻击方式不是对加密算法的攻击，而是针对算法的使用不当进行的攻击。
首先我们了解一下使用CBC模式加密敏感信息的服务器是怎么处理我们提交的内容的。假设我们向服务器提交了正确的密码，我们的密码在经过CBC模式加密后传给了服务器，这时服务器会对我们传来的信息尝试解密，如果可以正常解密会返回一个值表示正确，如果不能正常解密则会返回一个值表示错误。
而事实上，判断提交的密文能不能正常解密，第一步就是判断密文最后一组的填充值是否正确，
 也就是观察最后一组解密得到的结果的最后几位，
 如果错误将直接返回错误
，如果正确，再将解密后的结果与服务器存储的结果比对
，判断是不是正确的用户。也就是说服务器一共可能有三种判断结果
：
1.密文不能正常解密；
2.密文可以正常解密但解密结果不对；
3.密文可以正常解密并且解密结果比对正确；
其中第一种情况与第二 三种情况的返回值一定不一样
这就给了我们可乘之机——我们可以利用服务器的返回值判断我们提交的内容能不能正常解密，
 进一步讲，我们可以知道最后一组密文的填充位符不符合填充标准。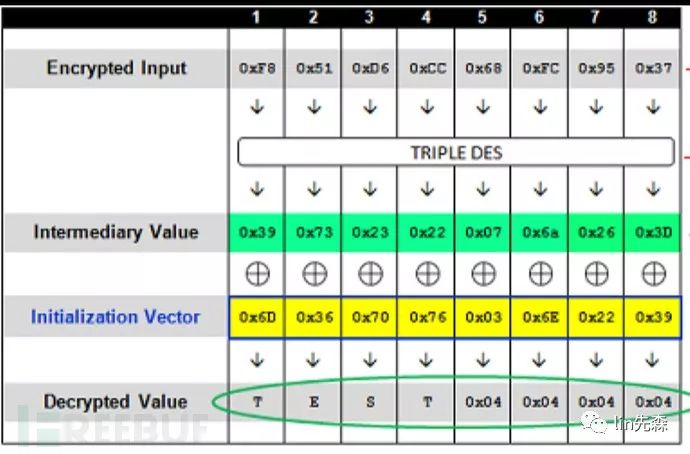


如上图所示，明文填充了四位时，如果最后一组密文解密后的结果（Intermediary Value也就是中间值）与前一组密文（Initialization Vector也就是IV值）异或得到的最后四位是0×04，那么服务器就会返回可以正常解密。

回忆一下前面我们说过的CBC模式的解密过程，第n组密文解密后的中间值与前一组的密文异或便可得到明文，
现在我们不知道解密的密钥key
但我们知道所有的密文
因此只要我们能够得到中间值便可以得到正确的密文（进行一次异或运算便可），而中间值是由服务器解密得到的
，因此我们虽然不知道怎么解密但我们可以利用服务器帮我们解密
 ，我们所要做的是能确定我们得到的中间值是正确的
，这也是padding oracle attack的核心——找出正确的中间值。

那么我们该如何利用服务器帮我们找到中间值呢？我们刚刚说过，服务器会根据我们提交的密文能否正确解密给我们返回不同的值
这里就有一个可以利用的逻辑判断，判断的标准是最后几位的填充值是否符合标准，
再回忆一下前面说的PKCS #5填充和CBC模式的解密过程，我们不难理解下面的攻击过程：
1.假设我们捕获到了传输的密文并且我们知道是CBC模式采用的什么加密算法，我们把密文按照加密算法的要求分好组，然后对倒数第二组密文进行构造；

2.先假定明文只填充了一字节，对倒数第二组密文的最后一字节从0×00到0xff逐个赋值并逐个向服务器提交，直到服务返回值表示构造后的密文可以正常解密，这意味着构造后的密文作为中间值（图中黄色的那一行）解密最后一组明文，明文的最后一位是0×01（如图所示），也就是说构造的倒数第二组密文的最后一字节与最后一组密文对应中间值（绿色的那一行）的最后一位相异或的结果是0×01；

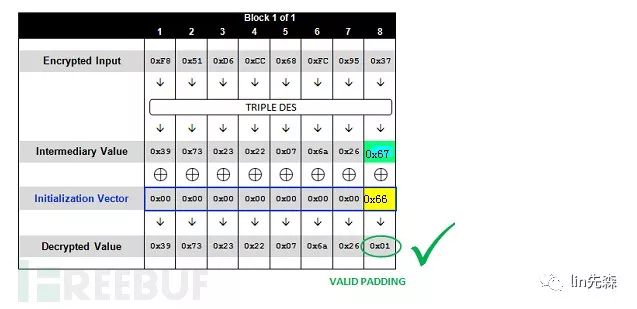
3.利用异或运算的性质，我们把我们构造的密文的最后一字节与0×01异或便可得到最后一位密文解密后的中间值是什么，这里我们设为M1，这一过程其实就是对应下图CBC解密过程中红圈圈出来的地方，1就是我们想要得到的中间值，二就是我们构造的密文也就是最后一组密文的IV值，我们已经知道了plaintext的最后一字节是0×01，从图中可以看到它是由我们构造的IV值与中间值的最后一字节异或得到的；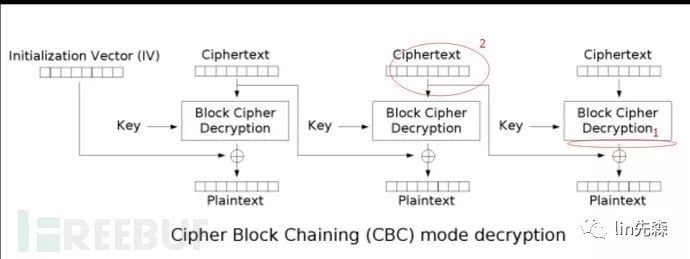

4.再假定明文填充了两字节也就是明文最后两字节是0×02，接着构造倒数第二组密文，我们把M1与0×02异或可以得到填充两字节时密文的最后一位应该是什么，这时候我们只需要对倒数第二位进行不断地赋值尝试（也是从0×00到0xff），当服务器返回值表示可以正常解密时，我们把此时的倒数第二位密文的取值与0×02异或便可得到最后一组密文倒数第二字节对应的中间值；

5.后再构造出倒数第三倒数第四直到得到最后一组密文的中间值，把这个中间值与截获的密文的倒数第二位异或便可得到最后一组分组的明文；

6.舍弃掉最后一组密文，只提交第一组到倒数第二组密文，通过构造倒数第三组密文得到倒数第二组密文的明文，最后我们便可以得到全部的明文

Padding oracle attack的关键思路就在于通过构造IV值（也就是前一组密文）利用服务器的返回值结合PKCS #5来找到正确的中间值，从而绕过加密算法，直接得到解密后的内容。
其实就是通过服务器的返回值判断自己构建的IV值对不对，进而猜测出正确的中间值Intermediary Value，中间值再和获取到的原本的IV值异或便可得到明文，因此攻击成立的两个重要假设前提:

攻击者能够获得密文（Ciphertext），以及附带在密文前面的IV（初始化向量）
攻击者能够触发密文的解密过程，且能够知道密文的解密结果

能够获得密文我们才能得到正确的明文，
而密文的第一组分组需要有正确的初始化向量才能解密。
能触发密文的解密过程才能在不知道密钥的情况下绕过加密算法直接得到我们需要的结果，
而知道密文的解密结果是通过服务器返回值来判断结果是不是符合填充标准来实现的，例如符合填充一位的话解密结果就是0×01，而我们正是通过把自己构造的IV值与解密结果异或才得到正确的中间值进而得到明文的。

如果我们输入一个错误的iv，依旧是可以解密的，但是middle和我们输入的iv经过异或后得到的填充值可能出现错误
比如本来应该是admin\x0b\x0b\x0b\x0b\x0b\x0b\x0b\x0b\x0b\x0b\x0b

而我们错误的得到admin\x0b\x0b\x0b\x0b\x0b\x0b\x0b\x0b\x0b\x3b\x2c

这样解密程序往往会抛出异常(Padding Error)

应用在web里的时候，往往是302或是500报错
而正常解密的时候是200
所以这时，我们可以根据服务器的反应来判断我们输入的iv
我们假设middle中间值为(为了方便，这里按8位分组来阐述)
0x39 0x73 0x23 0x22 0x07 0x6a 0x26 0x3d

正确的解密iv应该为
0x6d 0x36 0x70 0x76 0x03 0x6e 0x22 0x39

解密后正确的明文为：
T E S T 0x04 0x04 0x04 0x04

a=[0x6d,0x36,0x70,0x76,0x03,0x6e,0x22,0x39]
b=[0x39,0x73,0x23,0x22,0x07,0x6a,0x26,0x3d]
for i in range(8):
	print chr(a[i]^b[i])
T
E
S
T
<0x04>
<0x04>
<0x04>
<0x04>

但是关键点在于，我们可以知道iv的值，却不能得到中间值和解密后明文的值
而我们的目标是只根据我们输入的iv值和服务器的状态去判断出解密后明文的值
这里的攻击即叫做Padding Oracle Attack攻击

这时候我们选择进行爆破攻击
首先输入iv
0x00 0x00 0x00 0x00 0x00 0x00 0x00 0x00

这时候和中间值middle进行异或得到：
0x39 0x73 0x23 0x22 0x07 0x6a 0x26 0x3d

而此时程序会校验最后一位padding字节是否正确
我们知道正确的padding的值应该只有0x01~0x08，这里是0x3d，显然是错误的
所以程序会抛出500
知道这一点后，我们可以通过遍历最后一位iv，从而使这个iv和middle值异或后的最后一位是我们需要0x01
这时候有256种可能，不难遍历出
Iv:
0x00 0x00 0x00 0x00 0x00 0x00 0x00 0x3c

Middle:
0x39 0x73 0x23 0x22 0x07 0x6a 0x26 0x3d

两者异或后得到的是：
0x39 0x73 0x23 0x22 0x07 0x6a 0x26 0x01

这时候程序校验最后一位，发现是0x01，即可通过校验，服务器返回200
middle是不变的
我们根据这个200就可以判断出，这个iv正确了
然后我们有公式：

Middle[8]^原来的iv[8] = plain[8]
Middle[8]^现在的iv[8] = 0x01

故此，我们可以算出middle[8] = 0x01^现在的iv[8]

然后带入式1：
Plain[8] = 0x01^现在的iv[8]^原来的iv

即可获取明文plain[8]= 0x01^0x3c^0x39=0x04

和我们之前解密成功的明文一致（最后4位为填充）
下面我们需要获取plain[7]
方法还是如出一辙
但是这里需要将iv更新，因为这次我们需要的是2个0x02，而非之前的一个0x01
所以
又因为middle是不变的 最后一位变为0x02
所以iv的最后一位改变
所以我们需要将现在的iv[8] = middle[8]^0x02

因为现在的iv[8]^middle[8]=服务器校验的值

而我们遍历倒数第二位，应该是2个0x02，所以服务器希望得到的是0x02，所以

现在的iv[8]^middle[8]=0x02
故此iv[8] = middle[8]^0x02

然后再继续遍历现在的iv[7]
从0x00到0xff fuzz根据网页的响应
得到 iv[7]为0x24 ^ 0x02 得到 不变的 middle[7]
plain[7] 等于 不变的middle[7] ^ 截获的已有的原先的最开始的iv[7]
最后遍历循环，即可得到完整的plain