作者 | 谭军一
虽然过去不能改变,“未来” 可以 !
网页数据或者图像数据往往比较大,对于传输和存储都不太友好,我们在请求静态资源时能看到 Request Headers的accept-encoding 通常会包含 gzip, deflate, br 三种格式,其中 deflate 也是 PNG 图片的核心压缩算法,它主要是由 LZ77 算法与哈夫曼编码(Huffman Coding)组成的一个无损数据压缩算法,下面分别介绍它们的基础原理与 JS 部分算法实现。
1. LZ77 算法
1.1 算法简介
LZ77 算法是由 Lempel-Ziv 在 1977 发明的,其核心思想是比对相邻区域内的数据,获取数据中尽可能多的连续重复数据。然后使用坐标加长度的方式进行替换。LZ77 本身是较为简单却非常高效的压缩算法,为了获得更大的压缩比例,它与 Base64 进行配合使用。我们在学习 LZ77 时必须了解三个关键词:
滑动窗口: 指固定长度范围(窗口大小)的地址区间,窗口内存放输入流前的多个数据,每次循环窗口向右移动。
缓冲区: 预先读取一定长度的数据内容到缓冲区,用作与窗口数据进行对比。每次循环时与滑动窗口一起向右移动
字典: 滑动窗口内的字符可以组成多个字符串,这些字符串的组合称为字典。在滑动窗口跟随指针滑动过程中,字典跟随滑动窗口不断的改变。当缓冲区内的字符串能与窗口的字符串相匹配时则进行标记,被标记的字符串通过起始坐标,距离及下一个字符替换,所以通常我们将长度大于 3 个匹配的字符串才放入字典。例如 ABCD 中包含 ABC,BCD,ABCD 这三个。
1.2 LZ77 压缩
1.2.1 压缩原理
假如现在有一串字符 ABABCBABABCAD,设置缓冲区大小为 4,滑动窗口大小为 8 个字节。在初始时前四个字符 ABAB 进入缓冲区,滑动窗口为空,此时记录下一个字符 A

当窗口向右移动两个字符时,窗口内的AB和缓冲区的 AB 匹配,则进行标记替换,其中 6 表示 AB 在滑动窗口中的位置,2 表示匹配到的字符长度,C 为下一个字符。此时指针增加匹配长度 2

继续移动一个字符,发现匹配到 BAB,则继续添加匹配标识:

以此类推,直到匹配结束:

1.2.2 数据预处理
我们通常存储或者传输过程中为 16 进制数据或者字符,在编码时需要转换成对应的 ASICII码:
const str = 'ababcbababcadababcbababcadababcbababcadababcbababcadababcbababcadababcbababcadababcbababcadababcbababcadababcbababcadababcbababcadababcbababcadababcbababcad'
const arr = str.split('').map(char => char.charCodeAt())
得到结果:
[ 97, 98, 97, 98, 99, 98, 97, 98, 97, 98, 99, 97, 100, 97, 98, 97, 98, 99, 98, 97, 98, 97, 98, 99 ...]
1.2.3 滑动窗口压缩
压缩的比例,压缩的速度与滑动窗口和缓冲区的大小密切相关,通常被压缩的文件比较大,所以需要进行分片压缩,通常单片的大小为 64K,片与片之间不会进行窗口比较。扫描字符串开始编码, 移动编码原理见 1.1.2
var X = 1<<15 /* 距离用15位二进制表示*/
for(var i=0;i<str.length;i++)
{
var max_len=0, max_off=0;// 最长匹配和位置
if( i< str.length-3) {
var d1 = String.fromCharCode(str[i],str[i+1],str[i+2]); //三字节字符串加入索引
if(dic[d1]) {
dic[d1].push(i);
}else{
dic[d1] = [i];
}
for(var k=dic[d1].length-2; k>=0; k--) {
var j = dic[d1][k];
if(j <= i - X) {
break;
}
var len = strcmp(str, i, j); //在索引位置处查找最长匹配
if(len > max_len) {
max_len = len;
max_off = i - j;
}
}
}
...
}
实现 在字符串 str 中 比较 a,b 位置处的最长匹配:
var L = 32 /* 匹配长度用5位二进制*/;
function strcmp(str, a, b) {
var i = 0, sl = str.length;
for(;i< L && a+i<sl && b+i<sl;i++)
if(str[a+i] != str[b+i])
return i;
return i<L?i:L;
}
上面代码中,是否匹配的标识受分片大小 X 和 计算 max_len 得出。在整个计算过程中,需要存储的数据有三种:
匹配标志:用于表示是否为匹配成功
下一位字符:无论匹配成功或者失败都会存储下一位数据
起始位置:表示匹配数据在滑动窗口的地址索引
匹配长度:表示在进行压缩时替换的内容长度
由于一个字符的存储通常需要 2 个字符,这里使用 base64 进行编码压缩,具体的原理在前文已经讲过。所以这里采用 3 个字节存储 4 位 base64 编码。
if(max_off < X && max_len > 3) { // 找到最长匹配
write_bits(r, 1,1); // 写入标识
write_bits(r, max_off, 15); // 写入位置
write_bits(r, max_len-3, 5); // 写入长度
i+= max_len-1;
}else{
write_bits(r, 0,1); // 没找到 写入标识和原字符
write_bits(r, str[i], 8);
}
滑动窗口移动过程中,当未匹配到数据时:数据在内存中存储时采用 9 位二进制表示一位,第一位是标识位,用于表示是否匹配到可以替换的数据,未匹配到时为 0,后面的 8 位二进制表示一个字符。
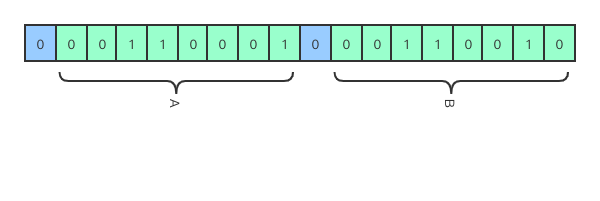
当匹配到数据时:数据标识位第一位改成 1,紧接着 15 位二进制用来表示滑动窗口中替换字符的偏移地址,5 位二进制表示替换数据的长度。
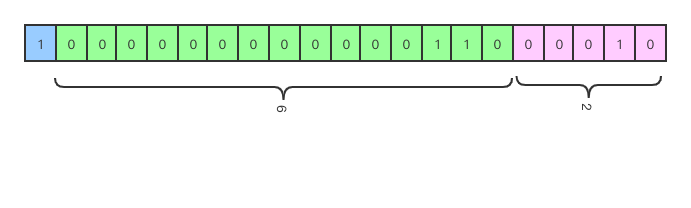
当超过 3 个字节时(24 位二进制)时,自动开辟 3 个字节的空间进行连续存储。
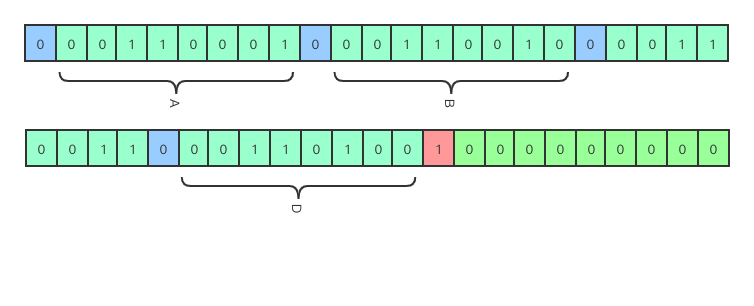
1.2.4 base64 压缩
将得到的压缩数据继续进行 base64 压缩
const base64Encode = (r)=>{
var z = "ABCDEFGHIJKLMNOPQRSTUVWXYZabcdefghijklmnopqrstuvwxyz0123456789+/=".split("");
var rs = [];
for(var i=0;i<r.length;i++) {
rs[rs.length] = z[(r[i]>>18) & 0x3f];
rs[rs.length] = z[(r[i]>>12) & 0x3f];
rs[rs.length] = z[(r[i]>> 6) & 0x3f];
rs[rs.length] = z[(r[i] ) & 0x3f];
}
return rs.join("");
}
得到的最终数据即 LZ77 压缩结果:AAASMJiMJiMZigAYRhMkAG9gCfsAg9gGjsBBMAAA。原字符串长度为 156,压缩后长度为 40,重复字符串越多,连续重复内容越长,压缩比越高。
1.3 数据解压
LZ77 算法解压是压缩的逆向过程,大概分为 base64 解密,滑动窗口数据还原,字符还原等过程。
1.3.1 base64 解码
const base64Decode = (s) => {
var i,j, ch, z ={}, w = 'ABCDEFGHIJKLMNOPQRSTUVWXYZabcdefghijklmnopqrstuvwxyz0123456789+/='.split('');
for(i=0;i<64;i++) // base64解码
z[w[i]] = i;
var r = [], x=1, y=0; // 将BASE64转为整型数组
for(i=0,j=0;i<s.length;i+=4,j++)
r[j] = (z[s.charAt(i)]<<18) | (z[s.charAt(i+1)]<<12) | (z[s.charAt(i+2)]<<6) | (z[s.charAt(i+3)]);
}
1.3.2 滑动窗口数据还原
读取压缩后的二进制数据,如果遇到标志为 0 则作为普通字符解析,如果为 1,则连续解析 2 位,分别为滑动窗口偏移位置和对应的数据长度。
for(;;) {
var c = read_bits(r, 1); // 读取一位标志位
if(c<0)break;
if(c==0){
s[s.length] = read_bits(r, 8);//读取一个字节
j++;
}else{
var off = read_bits(r, 15);// 位置
var len = read_bits(r, 5)+3; // 长度
for(var k=0;k<len;k++) { // copy
s[s.length]= s[j-off];
j++;
}
}
}
1.3.3 还原成字符串
通过上面的操作,我们已经得到了长度为 156 的数组,每位数据可以还原成一个字符。通过 String.fromCharCode 转换成原始字符串
function utf8_to_str(s) {
var r = [], fc = String.fromCharCode;
for(var i=0;i<s.length;i++) {
var ch = s[i];
if(ch< 0x80)
r[r.length] = fc(s[i]);
else if(ch < 0xE0) {
r[r.length] = fc( ((s[i]&0x1f) << 6) | (s[i+1] & 0x3f));
i++;
}else if(ch < 0xF0) {
r[r.length] = fc( ((s[i] & 0xF) << 12) | ((s[i+1] & 0x3f)<<6) | (s[i+2] & 0x3f));
i+=2;
}
}
return r.join('');
}
解压得到的字符串为:ababcbababcadababcbababcadababcbababcadababcbababcadababcbababcadababcbababcadababcbababcadababcbababcadababcbababcadababcbababcadababcbababcadababcbababcad,与压缩前数据一致。
2. 哈夫曼编码
2.1 算法简介
哈夫曼树(Huffman Tree),又称最优二叉树,是一类带权路径长度最短的树。假设有 n 个权值 {w1,w2,...,wn},如果构造一棵有 n 个叶子节点的二叉树,而这 n 个叶子节点的权值是 {w1,w2,...,wn},则所构造出的带权路径长度最小的二叉树就被称为哈夫曼树。
2.2 算法实现
我们现在有一串字符串 "hello world"。计算机中存储这段字符是通过 ASCII 码进行存储。
const str = "hello world";
const arr = str.split('').map(char => String.charAt(char))
得到该字符串在内存中存储内容为:
104, 101, 108, 108, 111, 32, 119, 111, 114, 108, 100
每一个字符在内存中占用两个字节,"hello world" 这个字符串则一共占用了 22 个字节。下面我们开始进行数据压缩
哈夫曼编码的思想是提取内容中频率最高的字符,使用最短的编码来替代。我们称每个元素出现的频率为权重,计算上面字符的权重并且排序。
// 获取权重
const getWeight = (arr) => {
const obj = {};
arr.forEach(char => {
obj[char] = obj[char] ? obj[char] + 1 : 1
})
console.log("wight:", obj)
return obj;
}
// 按权重排序
const sort = (wightObj) => {
let arr = Object.keys(wightObj).map(key => ({
data: key,
wight: wightObj[key]
}))
let sortArr = arr.sort((a, b) => a.wight > b.wight ? 1 : -1)
console.log(sortArr)
}
// 排序计算结果:
[
{ data: '119', wight: 1 },
{ data: '114', wight: 1 },
{ data: '104', wight: 1 },
{ data: '101', wight: 1 },
{ data: '100', wight: 1 },
{ data: '32', wight: 1 },
{ data: '111', wight: 2 },
{ data: '108', wight: 3 }
]
2.1.1 构建哈夫曼树
上面的字符 l 使用二进制的 1 来替代,则内存占用仅仅为原来的 1/16 。但是其他字符不能再用二进制的 1 来表示,而且在解码的时候如果二进制 11 表示了另一个字符,则无法区分 1 和 11 的情况。为了解决上述问题,我们构造哈夫曼树。
哈夫曼树也叫做最优二叉树,构建哈夫曼树的两大原则:
权重越高的点离根节点越近,权重越低的点离根结点越远
同一父节点对应的两个字节点,左边节点的权重低于右边节点。
在上面这组权重数据:1,1,1,1,1,1,2,3。拼装的结果如图
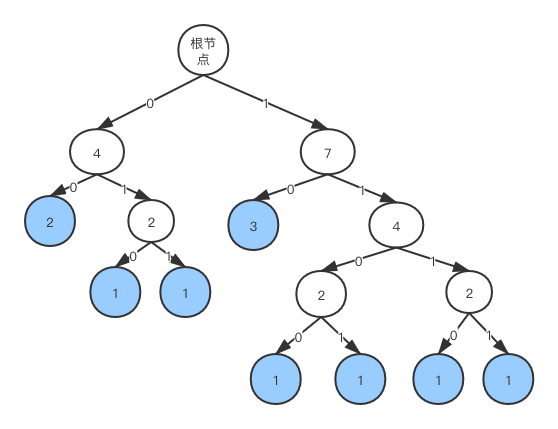
代码实现哈夫曼树构建:
// 制造hafuman树
const makeTree = (arr) => {
while (arr.length > 1) {
// 取数组中最小的两个
let [node1, node2] = arr.splice(0, 2);
let node = {
wight: 0 + node1.wight + node2.wight,
children: [node1, node2]
}
arr.push(node);
arr = arr.sort((a, b) => a.wight > b.wight ? 1 : -1)
console.log(arr.length)
}
return arr[0];
}
2.1.2 哈夫曼对照表
通过哈夫曼树进行递归遍历,找到对应节点时所经过的所有路径即最优编码,最终将所有元素与路径的一一关系组成哈夫曼对照表。
const map = {};
const makeMap = (node, path) => {
if (node.children) {
node.children.forEach((child, index) => makeMap(child, path + index))
} else {
map[node.code] = path
}
}
得到结果:
{
"32": "1100",
"100": "1101",
"101": "001",
"104": "000",
"108": "10",
"111": "111",
"114": "011",
"119": "010"
}
通过哈夫曼对照表即可进行数据加密:
const encode = (charList) => {
const wightObj = getWeight(charList)// 计算权重
const nodeList = sort(wightObj)// 获取节点列表
const tree = makeTree(nodeList);//获取哈夫曼树
makeMap(tree, '');//获取对照表
let str = '';
charList.forEach(char => str += map[char])
return str;
}
得到加密后的结果为:00000110101111100010111011101101。共 32 位二进制,占用 4 个字节。实际文件压缩或者网络传输过程中,除了被压缩的内容还包含哈夫曼对照表等其他数据,一般情况当文件小于 200 字节时压缩的结果反而会比源文件更大。
2.3 哈夫曼解码
获取到哈夫曼对照表及编码数据之后进行解码是非常容易的,设置临时变量 temp 作为移动窗口,与哈夫曼对照表的值进行一一对比,如果对比失败则 temp 添加一位继续对比。如果其中某一位数据出错,则直接会对比失败,一般都会对数据进行校验。通常会用较为简单的循环冗余校验 CRC。
// 哈夫曼对照表 键值对互换位置
const traversal = (map) => {
let obj = {}
Object.keys(map).forEach(key => {
obj[map[key]] = key;
})
return obj;
}
// 解码
const decode = (code) => {
let str = '', temp = '';
let decodeMap = traversal(map);
for (var i = 0; i < code.length; i++) {
temp += code[i];
if (decodeMap[temp]) {
str += String.fromCodePoint(decodeMap[temp]);
temp = ''
}
}
return str;
}
最终得到的解码结果:hello world,与原字符一致。
defleate 算法先通过 LZ77 算法压缩,然后在用哈夫曼算法进行压缩。两种算法都有很多变体版本,但是整体思路大同小异,值得我们学习。
全文完
以下文章您可能也会感兴趣:
我们正在招聘 Java 工程师,欢迎有兴趣的同学投递简历到 rd-hr@xingren.com 。







