






算法本质。没人敢说强化学习不行,但很多人却觉得群智能很水,东西很牛逼,但是由于门槛低,几乎不需要啥计算机编程基础,不懂的水货多了,拉低整个档次。
算法局限。相比于传统算法,如果只靠进化算法计算,求解效率是真的低,需要针对问题设计特定的启发式因子用以改进算法(难点)。
算法应用。随机性算法,可以求解任何问题,应用领域极其广泛。
算法改进。种群初始化、全局搜索策略、局部搜索策略、不同算法缝合(其实也是全局与局部搜索的变化)。
算法创新。应用的背景(是否落地)决定了群智能算法的上限,针对特定问题设计特定算法才是核心中的核心,难点中的难点。取悦测试集不如有效解决一个应用
暂时就想到了这些 ,后面再接着补充吧,后面会将群智能开源系列一直更新下去,所提供的思路、代码仅作参考。
,后面再接着补充吧,后面会将群智能开源系列一直更新下去,所提供的思路、代码仅作参考。
1
麻雀搜索算法简介
发现者通常拥有较高的能源储备并且在整个种群中负责搜索到具有丰富食物的区域,为所有的加入者提供觅食的区域和方向。在模型建立中能量储备的高低取决于麻雀个体所对应的适应度值(Fitness Value)的好坏。
发现了捕食者,个体开始发出鸣叫作为报警信号。当报警值大于安全值时,发现者会将加入者带到其它安全区域进行觅食。
发现者和加入者的身份是动态变化的。
加入者的能量越低,它们在整个种群中所处的觅食位置就越差。
在觅食过程中,加入者总是能够搜索到提供最好食物的发现者,然后从最好的食物中获取食物或者在该发现者周围觅食。
当意识到危险时,群体边缘的麻雀会迅速向安全区域移动,以获得更好的位置,位于种群中间的麻雀则会随机走动,以靠近其它麻雀。
1.2算法设计(更新)
(1)n只麻雀组成的种群公式如下
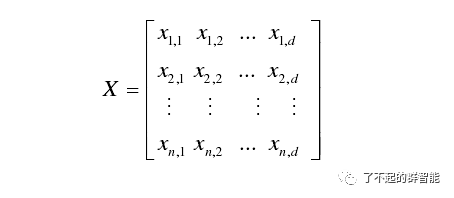
(2)麻雀适应度值f(d维)
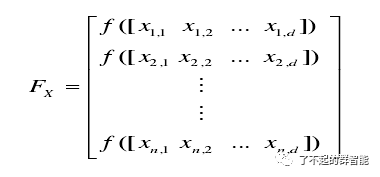
(3)发现者位置更新(占比20%)

(4)加入者位置更新

式中,A表示一个1Xd的矩阵,每个元素随机赋值1或-1,且
(5)预警麻雀(10%-20%)位置更新公式

1.3 算法伪代码(流程)

2
麻雀搜索算法源代码(中文注释)
ssa_main.m
% -----------------------------------------------------------------------------------------------------------% Sparrow Search algorithm (SSA) (demo)% Programmed by Jian-kai Xue% Updated 21 Mar, 2020.%% This is a simple demo version only implemented the basic% idea of the SSA for solving the unconstrained problem.% The details about SSA are illustratred in the following paper.% (To cite this article):% Jiankai Xue & Bo Shen (2020) A novel swarm intelligence optimization% approach: sparrow search algorithm, Systems Science & Control Engineering, 8:1, 22-34, DOI:% 10.1080/21642583.2019.1708830clear allclcSearchAgents_no=100; % 代数Function_name='F1'; % Name of the test function that can be from F1 to F23 (Table 1,2,3 in the paper)Max_iteration=1000; % Maximum numbef of iterations% Load details of the selected benchmark function[lb,ub,dim,fobj]=Get_Functions_details(Function_name);[fMin,bestX,SSA_curve]=SSA(SearchAgents_no,Max_iteration,lb,ub,dim,fobj);%Draw objective spacefigure('Position',[500 500 600 300])subplot(1,2,1);func_plot(Function_name);title('基准函数三维图')xlabel('x_1');ylabel('x_2');zlabel([Function_name,'( x_1 , x_2 )'])grid onbox onsubplot(1,2,2);semilogy(SSA_curve,'Color','g')axis ([0 1000 0 1 ])title('Objective space')xlabel('Iteration');ylabel('Best score obtained so far');%axis tightgrid onbox onlegend('SSA')display(['The best solution obtained by SSA is : ', num2str(bestX)]);display(['The best optimal value of the objective funciton found by SSA is : ', num2str(fMin)]);
SSA.m
%pop是种群,M是迭代次数,fobj是用来计算适应度的函数%pNum是生产者function [fMin , bestX,Convergence_curve ] = SSA(pop, M,c,d,dim,fobj )P_percent = 0.2; % The population size of producers accounts for "P_percent" percent of the total population size%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%pNum = round( pop * P_percent ); % The population size of the producerslb= c.*ones( 1,dim ); % Lower limit/bounds/ a vectorub= d.*ones( 1,dim ); % Upper limit/bounds/ a vector%Initializationfor i = 1 : popx( i, : ) = lb + (ub - lb) .* rand( 1, dim );fit( i ) = fobj( x( i, : ) ) ;endpFit = fit;pX = x; % The individual's best position corresponding to the pFit[ fMin, bestI ] = min( fit ); % fMin denotes the global optimum fitness valuebestX = x( bestI, : ); % bestX denotes the global optimum position corresponding to fMin% Start updating the solutions.%for t = 1 : M[ ans, sortIndex ] = sort( pFit );% Sort.[fmax,B]=max( pFit );worse= x(B,:);r2=rand(1);%%%%%%%%%%%%%5%%%%%%这一部位为发现者(探索者)的位置更新%%%%%%%%%%%%%%%%%%%%%%%%%if(r2<0.8)%预警值较小,说明没有捕食者出现for i = 1 : pNum %r2小于0.8的发现者的改变(1-20) % Equation (3)r1=rand(1);x( sortIndex( i ), : ) = pX( sortIndex( i ), : )*exp(-(i)/(r1*M));%对自变量做一个随机变换x( sortIndex( i ), : ) = Bounds( x( sortIndex( i ), : ), lb, ub );%对超过边界的变量进行去除fit( sortIndex( i ) ) = fobj( x( sortIndex( i ), : ) ); %计算新的适应度值endelse %预警值较大,说明有捕食者出现威胁到了种群的安全,需要去其它地方觅食for i = 1 : pNum %r2大于0.8的发现者的改变x( sortIndex( i ), : ) = pX( sortIndex( i ), : )+randn(1)*ones(1,dim);x( sortIndex( i ), : ) = Bounds( x( sortIndex( i ), : ), lb, ub );fit( sortIndex( i ) ) = fobj( x( sortIndex( i ), : ) );endend[ fMMin, bestII ] = min( fit );bestXX = x( bestII, : );%%%%%%%%%%%%%5%%%%%%这一部位为加入者(追随者)的位置更新%%%%%%%%%%%%%%%%%%%%%%%%%for i = ( pNum + 1 ) : pop %剩下20-100的个体的变换 % Equation (4)A=floor(rand(1,dim)*2)*2-1;if( i>(pop/2))%这个代表这部分麻雀处于十分饥饿的状态(因为它们的能量很低,也是是适应度值很差),需要到其它地方觅食x( sortIndex(i ), : )=randn(1)*exp((worse-pX( sortIndex( i ), : ))/(i)^2);else%这一部分追随者是围绕最好的发现者周围进行觅食,其间也有可能发生食物的争夺,使其自己变成生产者x( sortIndex( i ), : )=bestXX+(abs(( pX( sortIndex( i ), : )-bestXX)))*(A'*(A*A')^(-1))*ones(1,dim);endx( sortIndex( i ), : ) = Bounds( x( sortIndex( i ), : ), lb, ub );%判断边界是否超出fit( sortIndex( i ) ) = fobj( x( sortIndex( i ), : ) );%计算适应度值end%%%%%%%%%%%%%5%%%%%%这一部位为意识到危险(注意这里只是意识到了危险,不代表出现了真正的捕食者)的麻雀的位置更新%%%%%%%%%%%%%%%%%%%%%%%%%c=randperm(numel(sortIndex));%%%%%%%%%这个的作用是在种群中随机产生其位置(也就是这部分的麻雀位置一开始是随机的,意识到危险了要进行位置移动,%处于种群外围的麻雀向安全区域靠拢,处在种群中心的麻雀则随机行走以靠近别的麻雀)b=sortIndex(c(1:20));for j = 1 : length(b) % Equation (5)if( pFit( sortIndex( b(j) ) )>(fMin) ) %处于种群外围的麻雀的位置改变x( sortIndex( b(j) ), : )=bestX+(randn(1,dim)).*(abs(( pX( sortIndex( b(j) ), : ) -bestX)));else %处于种群中心的麻雀的位置改变x( sortIndex( b(j) ), : ) =pX( sortIndex( b(j) ), : )+(2*rand(1)-1)*(abs(pX( sortIndex( b(j) ), : )-worse))/ ( pFit( sortIndex( b(j) ) )-fmax+1e-50);endx( sortIndex(b(j) ), : ) = Bounds( x( sortIndex(b(j) ), : ), lb, ub );fit( sortIndex( b(j) ) ) = fobj( x( sortIndex( b(j) ), : ) );endfor i = 1 : popif ( fit( i ) < pFit( i ) )pFit( i ) = fit( i );pX( i, : ) = x( i, : );endif( pFit( i ) < fMin )fMin= pFit( i );bestX = pX( i, : );endendConvergence_curve(t)=fMin;end% Application of simple limits/boundsfunction s = Bounds( s, Lb, Ub)% Apply the lower bound vectortemp = s;I = temp < Lb;temp(I) = Lb(I);% Apply the upper bound vectorJ = temp > Ub;temp(J) = Ub(J);% Update this new moves = temp;%---------------------------------------------------------------------------------------------------------------------------
Get_Functions_details(PRO)
% lb is the lower bound: lb=[lb_1,lb_2,...,lb_d]% up is the uppper bound: ub=[ub_1,ub_2,...,ub_d]% dim is the number of variables (dimension of the problem)function [lb,ub,dim,fobj] = Get_Functions_details(F)switch Fcase 'F1'fobj = @F1;lb=-100;ub=100;dim=30;case 'F2'fobj = @F2;lb=-10;ub=10;dim=30;case 'F3'fobj = @F3;lb=-100;ub=100;dim=30;case 'F4'fobj = @F4;lb=-100;ub=100;dim=30;case 'F5'fobj = @F5;lb=-30;ub=30;dim=30;case 'F6'fobj = @F6;lb=-100;ub=100;dim=30;case 'F7'fobj = @F7;lb=-1.28;ub=1.28;dim=30;case 'F8'fobj = @F8;lb=-500;ub=500;dim=30;case 'F9'fobj = @F9;lb=-5.12;ub=5.12;dim=30;case 'F10'fobj = @F10;lb=-32;ub=32;dim=30;case 'F11'fobj = @F11;lb=-600;ub=600;dim=30;case 'F12'fobj = @F12;lb=-50;ub=50;dim=30;case 'F13'fobj = @F13;lb=-50;ub=50;dim=30;case 'F14'fobj = @F14;lb=-65.536;ub=65.536;dim=2;case 'F15'fobj = @F15;lb=-5;ub=5;dim=4;case 'F16'fobj = @F16;lb=-5;ub=5;dim=2;case 'F17'fobj = @F17;lb=[-5,0];ub=[10,15];dim=2;case 'F18'fobj = @F18;lb=-2;ub=2;dim=2;case 'F19'fobj = @F19;lb=0;ub=1;dim=3;case 'F20'fobj = @F20;lb=0;ub=1;dim=6;case 'F21'fobj = @F21;lb=0;ub=10;dim=4;case 'F22'fobj = @F22;lb=0;ub=10;dim=4;case 'F23'fobj = @F23;lb=0;ub=10;dim=4;endend% F1function o = F1(x)o=sum(x.^2);end% F2function o = F2(x)o=sum(abs(x))+prod(abs(x));end% F3function o = F3(x)dim=size(x,2);o=0;for i=1:dimo=o+sum(x(1:i))^2;endend% F4function o = F4(x)o=max(abs(x));end% F5function o = F5(x)dim=size(x,2);o=sum(100*(x(2:dim)-(x(1:dim-1).^2)).^2+(x(1:dim-1)-1).^2);end% F6function o = F6(x)o=sum(abs((x+.5)).^2);end% F7function o = F7(x)dim=size(x,2);o=sum([1:dim].*(x.^4))+rand;end% F8function o = F8(x)o=sum(-x.*sin(sqrt(abs(x))));end% F9function o = F9(x)dim=size(x,2);o=sum(x.^2-10*cos(2*pi.*x))+10*dim;end% F10function o = F10(x)dim=size(x,2);o=-20*exp(-.2*sqrt(sum(x.^2)/dim))-exp(sum(cos(2*pi.*x))/dim)+20+exp(1);end% F11function o = F11(x)dim=size(x,2);o=sum(x.^2)/4000-prod(cos(x./sqrt([1:dim])))+1;end% F12function o = F12(x)dim=size(x,2);o=(pi/dim)*(10*((sin(pi*(1+(x(1)+1)/4)))^2)+sum((((x(1:dim-1)+1)./4).^2).*...(1+10.*((sin(pi.*(1+(x(2:dim)+1)./4)))).^2))+((x(dim)+1)/4)^2)+sum(Ufun(x,10,100,4));end% F13function o = F13(x)dim=size(x,2);o=.1*((sin(3*pi*x(1)))^2+sum((x(1:dim-1)-1).^2.*(1+(sin(3.*pi.*x(2:dim))).^2))+...((x(dim)-1)^2)*(1+(sin(2*pi*x(dim)))^2))+sum(Ufun(x,5,100,4));end% F14function o = F14(x)aS=[-32 -16 0 16 32 -32 -16 0 16 32 -32 -16 0 16 32 -32 -16 0 16 32 -32 -16 0 16 32;,...-32 -32 -32 -32 -32 -16 -16 -16 -16 -16 0 0 0 0 0 16 16 16 16 16 32 32 32 32 32];for j=1:25bS(j)=sum((x'-aS(:,j)).^6);endo=(1/500+sum(1./([1:25]+bS))).^(-1);end% F15function o = F15(x)aK=[.1957 .1947 .1735 .16 .0844 .0627 .0456 .0342 .0323 .0235 .0246];bK=[.25 .5 1 2 4 6 8 10 12 14 16];bK=1./bK;o=sum((aK-((x(1).*(bK.^2+x(2).*bK))./(bK.^2+x(3).*bK+x(4)))).^2);end% F16function o = F16(x)o=4*(x(1)^2)-2.1*(x(1)^4)+(x(1)^6)/3+x(1)*x(2)-4*(x(2)^2)+4*(x(2)^4);end% F17function o = F17(x)o=(x(2)-(x(1)^2)*5.1/(4*(pi^2))+5/pi*x(1)-6)^2+10*(1-1/(8*pi))*cos(x(1))+10;end% F18function o = F18(x)o=(1+(x(1)+x(2)+1)^2*(19-14*x(1)+3*(x(1)^2)-14*x(2)+6*x(1)*x(2)+3*x(2)^2))*...(30+(2*x(1)-3*x(2))^2*(18-32*x(1)+12*(x(1)^2)+48*x(2)-36*x(1)*x(2)+27*(x(2)^2)));end% F19function o = F19(x)aH=[3 10 30;.1 10 35;3 10 30;.1 10 35];cH=[1 1.2 3 3.2];pH=[.3689 .117 .2673;.4699 .4387 .747;.1091 .8732 .5547;.03815 .5743 .8828];o=0;for i=1:4o=o-cH(i)*exp(-(sum(aH(i,:).*((x-pH(i,:)).^2))));endend% F20function o = F20(x)aH=[10 3 17 3.5 1.7 8;.05 10 17 .1 8 14;3 3.5 1.7 10 17 8;17 8 .05 10 .1 14];cH=[1 1.2 3 3.2];pH=[.1312 .1696 .5569 .0124 .8283 .5886;.2329 .4135 .8307 .3736 .1004 .9991;....2348 .1415 .3522 .2883 .3047 .6650;.4047 .8828 .8732 .5743 .1091 .0381];o=0;for i=1:4o=o-cH(i)*exp(-(sum(aH(i,:).*((x-pH(i,:)).^2))));endend% F21function o = F21(x)aSH=[4 4 4 4;1 1 1 1;8 8 8 8;6 6 6 6;3 7 3 7;2 9 2 9;5 5 3 3;8 1 8 1;6 2 6 2;7 3.6 7 3.6];cSH=[.1 .2 .2 .4 .4 .6 .3 .7 .5 .5];o=0;for i=1:5o=o-((x-aSH(i,:))*(x-aSH(i,:))'+cSH(i))^(-1);endend% F22function o = F22(x)aSH=[4 4 4 4;1 1 1 1;8 8 8 8;6 6 6 6;3 7 3 7;2 9 2 9;5 5 3 3;8 1 8 1;6 2 6 2;7 3.6 7 3.6];cSH=[.1 .2 .2 .4 .4 .6 .3 .7 .5 .5];o=0;for i=1:7o=o-((x-aSH(i,:))*(x-aSH(i,:))'+cSH(i))^(-1);endend% F23function o = F23(x)aSH=[4 4 4 4;1 1 1 1;8 8 8 8;6 6 6 6;3 7 3 7;2 9 2 9;5 5 3 3;8 1 8 1;6 2 6 2;7 3.6 7 3.6];cSH=[.1 .2 .2 .4 .4 .6 .3 .7 .5 .5];o=0;for i=1:10o=o-((x-aSH(i,:))*(x-aSH(i,:))'+cSH(i))^(-1);endendfunction o=Ufun(x,a,k,m)o=k.*((x-a).^m).*(x>a)+k.*((-x-a).^m).*(x<(-a));end
3
麻雀搜索算法在基准函数上测试仿真
简单测试了几个函数(详细的测试可参考原作者的硕士论文以及已发表的sci),相关文献均在后面给出。
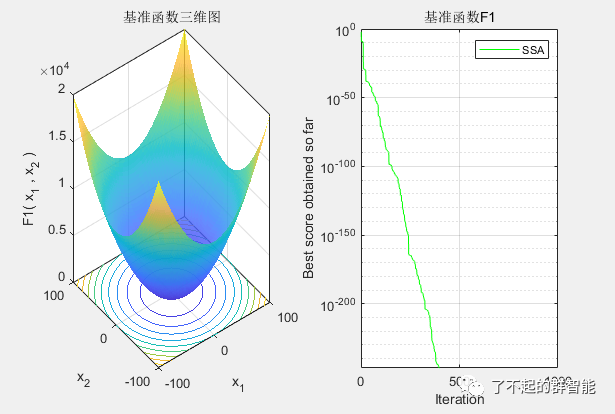
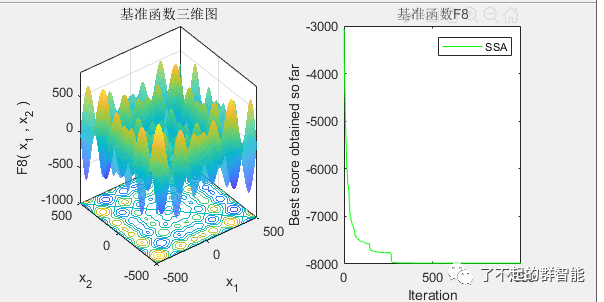
4
参考文献(含知网见刊,英文未统计)
[1]Xue J, Shen B . A novel swarm intelligence optimization approach: sparrow search algorithm[J]. Systems Science & Control Engineering An Open Access Journal, 2020, 8(1):22-34.
[1]吴新忠,韩正化,魏连江,左玉晓,许嘉琳,李昂.矿井风流智能按需调控算法与关键技术[J].中国矿业大学学报,2021,50(04):725-734.
[2]陈颖,刘峥莹,肖春艳,赵学亮,李康,庞丽丽,史彦新,李少华.基于麻雀搜索算法的土壤重金属X射线荧光光谱重叠峰解析[J].光谱学与光谱分析,2021,41(07):2175-2180.
[3]吴丁杰,周庆兴,温立书.基于Logistic混沌映射的改进麻雀算法[J].高师理科学刊,2021,41(06):10-15.
[4]刘栋,魏霞,王维庆,叶家豪,任俊.基于SSA-ELM的短期风电功率预测[J].智慧电力,2021,49(06):53-59+123.
[5]刘电霆,吴丹玲,黄康政.协作设计众包任务优化分配建模与求解[J].机械设计,2021,38(06):124-132.
[6]谷小兵,李建强,孟智超,王勐,陶君.基于改进FCM的脱硫系统优化运行策略[J/OL].华北电力大学学报(自然科学版),{3},{4}{5}:1-7[2021-07-19].http://kns.cnki.net/kcms/detail/13.1212.TM.20210616.1628.002.html.
[7]江妍,马瑜,梁远哲,王原,李光昊,马鼎.基于分数阶麻雀搜索优化OTSU肺组织分割算法[J].计算机科学,2021,48(S1):28-32.
[8]韩统,汤安迪,周欢,徐登武,谢磊.基于LASSA算法的多无人机协同航迹规划方法[J/OL].系统工程与电子技术,{3},{4}{5}:1-12[2021-07-19].http://kns.cnki.net/kcms/detail/11.2422.TN.20210601.0932.004.html.
[9]段玉先,刘昌云.基于Sobol序列和纵横交叉策略的麻雀搜索算法[J/OL].计算机应用,{3},{4}{5}:1-9[2021-07-19].http://kns.cnki.net/kcms/detail/51.1307.TP.20210525.1453.002.html.
[10]王海瑞,鲜于建川.改进麻雀搜索算法在分布式电源配置中的应用[J/OL].计算机工程与应用,{3},{4}{5}:1-9[2021-07-19].http://kns.cnki.net/kcms/detail/11.2127.TP.20210520.1039.004.html.
[11]李怡,李焕锋,刘自然.基于CEEMDAN多尺度熵和SSA-SVM的滚动轴承故障诊断研究[J].机电工程,2021,38(05):599-604.
[12]柳长安,冯雪菱,孙长浩,赵丽娟.基于改进麻雀算法的最大二维熵分割方法[J/OL].激光技术,{3},{4}{5}:1-15[2021-07-19].http://kns.cnki.net/kcms/detail/51.1125.tn.20210423.1018.004.html.
[13]马梦珂,倪静.基于度值和聚类系数的跨单元调度问题优化[J/OL].计算机应用研究,{3},{4}{5}:1-7[2021-07-19].https://doi.org/10.19734/j.issn.1001-3695.2021.01.0024.
[14]王禹,韩爽,王其乐,刘永前.以变桨轴承延寿为目标的风电机组变桨策略优化研究[J].分布式能源,2021,6(02):32-39.
[15]马晨佩,李明辉,巩强令,杨白月.基于麻雀搜索算法优化支持向量机的滚动轴承故障诊断[J].科学技术与工程,2021,21(10):4025-4029.
[16]毛清华,张强,毛承成,柏嘉旋.混合正弦余弦算法和Lévy飞行的麻雀算法[J/OL].山西大学学报(自然科学版),{3},{4}{5}:1-6[2021-07-19].https://doi.org/10.13451/j.sxu.ns.2020135.
[17]杨玮,杨白月,王晓雅,马晨佩,吴莹莹.低碳环境下冷链物流企业库存-配送优化[J].包装工程,2021,42(11):45-52.
[18]李黄曼,张勇,张瑶.基于ISSA优化SVM的变压器故障诊断研究[J].电子测量与仪器学报,2021,35(03):123-129.
[19]温泽宇,谢珺,谢刚,续欣莹.基于新型拥挤度距离的多目标麻雀搜索算法[J/OL].计算机工程与应用,{3},{4}{5}:1-10[2021-07-19].http://kns.cnki.net/kcms/detail/11.2127.TP.20210311.1136.008.html.
[20]李敦桥.一种混合麻雀搜索算法[J].电脑知识与技术,2021,17(05):232-234.
[21]聂晓明,高鹏翔.基于用户偏好和麻雀搜索聚类的协同过滤算法[J].青岛大学学报(自然科学版),2021,34(01):70-76.
[22]杜晔,王子萌,黎妹红.基于优化核极限学习机的工控入侵检测方法[J].信息网络安全,2021,21(02):1-9.
[23]欧阳城添,朱东林.融合K-means的多策略改进麻雀搜索算法研究[J/OL].电光与控制,{3},{4}{5}:1-9[2021-07-19].http://kns.cnki.net/kcms/detail/41.1227.tn.20210127.0910.004.html.
[24]史春天,曾艳阳,侯守明.群体智能算法在图像分割中的应用综述[J].计算机工程与应用,2021,57(08):36-47.
[25]毛清华,张强.融合柯西变异和反向学习的改进麻雀算法[J].计算机科学与探索,2021,15(06):1155-1164.
[26]汤安迪,韩统,徐登武,谢磊.基于混沌麻雀搜索算法的无人机航迹规划方法[J/OL].计算机应用,{3},{4}{5}:1-11[2021-07-19].http://kns.cnki.net/kcms/detail/51.1307.TP.20201124.1519.002.html.
[27]赵普凡,王伟.基于动态路径规划的车载自组织网络贪婪路由协议[J].国外电子测量技术,2020,39(11):46-51.
[28]吕鑫,慕晓冬,张钧.基于改进麻雀搜索算法的多阈值图像分割[J].系统工程与电子技术,2021,43(02):318-327.
[29]李雅丽,王淑琴,陈倩茹,王小钢.若干新型群智能优化算法的对比研究[J].计算机工程与应用,2020,56(22):1-12.
[30]吕鑫,慕晓冬,张钧,王震.混沌麻雀搜索优化算法[J/OL].北京航空航天大学学报,{3},{4}{5}:1-10[2021-07-19].https://doi.org/10.13700/j.bh.1001-5965.2020.0298.
[31]薛建凯. 一种新型的群智能优化技术的研究与应用[D].东华大学,2020.
5
代码获取方式
后台回复“SSA”
改进思路以及推荐阅读的文献可以后台留言
下期更新相关应用以及“海洋捕食者算法”







