数组相对其它结构比较简单,甚至很多人要跳槽时,不会专门去复习数组,这里只列出时间复杂度,然后给出几个leetcode关于数组的例子。
数组操作
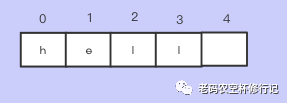
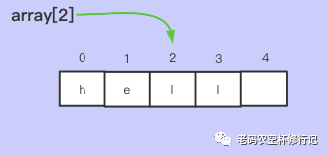
查询:通过下标索引直接定位,所以复杂度为 O(1)
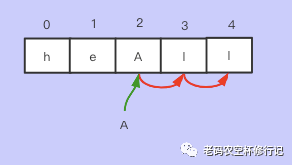
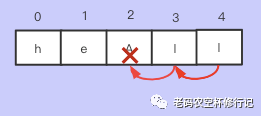
删除:删除元素后面几个就得移动几个,所以复杂度 O(n)
leetcode
你可以假设每种输入只会对应一个答案。但是,数组中同一个元素在答案里不能重复出现。
你可以按任意顺序返回答案。
数组是整数数组 数组里可能有两个数的和为目标 target 结果返回的是下标,不是哪两个加数 每个输入target值对应一个答案 两个加数在数组中的索引不能一样
func twoSum(nums []int, target int) []int {数组的长度, 一般底层通过专门的变量来存储长度所以其时间复杂度为 O(1)lens := len(nums)for i:=0; i<lens-1; i++ {求另外一个加数tmp := target - nums[i]从当前元素的后面开始找该加数寻找的时间复杂度为 O(n)当然这里如果数组特别长,可以二分查找等加速,但是这里考察的是数组,因此暂时不用考虑for j:=i+1; j<lens; j++ {if nums[j] == tmp {题目中讲到每种输入只对应一个答案因此只要符合条件,返回即可return []int{i, j}}}}return nil}
题目2:15. 三数之和
注意:答案中不可以包含重复的三元组。
这道题是两数之和的晋级,难度提升了不少,看看题目要点
a + b + c = 0, 数组中找出3个不同位置元素的和为0, 就是说 target=0 结果集不能相互重复
若第一个数大于0,后面的就无需计算 第一个数为三元组第一个元素,那么三元组的第二个和第三个可以通过“两端夹逼法” 计算,若是和大于0,说明第三个数太大,夹逼法的右边指针左移,若是和小于0,说明第二个数太小,夹逼法的左指针右移
func threeSum(nums []int) [][]int {size := len(nums)if size < 3 {return nil}// 预分配一定的空间,保证不频繁开空间导致的额外开销res := make([][]int, 0, 5)// 排好序,从小到大排序sort.Ints(nums)// size-2,三数之和, 保证当前元素后面流出2个元素for i:=0; i<size-2; i++ {// nums[i] > 0: 已经排好序,第一个数都大于0,那么后面加起来肯定大于0,直接跳过// i>0 && nums[i]==nums[i-1]: 说明当前这个数已经在上次循环中计算过了if nums[i] > 0 || (i>0 && nums[i] == nums[i-1]) {continue}// 另外两个数采用 “两端夹逼法"j, k := i+1, size-1for j < k {// 求和sum := nums[i] + nums[j] + nums[k]if sum == 0 {// 添加结果res = append(res, []int{nums[i], nums[j], nums[k]})// 向中间逼近,nums[j-1] == nums[j] 还是要排除重复的,否则// 重复计算会导致超时j++for j<k && nums[j-1] == nums[j] {j++}// 向中间逼近, nums[k] == nums[k+1] 还是要排除重复的,否则// 重复计算会导致超时k--for j<k && nums[k] == nums[k+1] {k--}} else if sum > 0 {// sum > 0 表示右边的数太大,应当缩小,所以索引 k 向// 左边移动,同时移动过程中应当过滤掉已经计算过的数,也就// 是 num[k] == num[k-1]k--for j<k && nums[k] == nums[k+1] {k--}} else {// sum < 0 表示左边的数太小,应当增大,所以索引 j 向// 右边移动,同时移动过程中应当过滤掉已经计算过的数,也就// 是 num[j] == num[j+1]j++for j<k && nums[j-1] == nums[j] {j++}}}}return res}
题目3:283.移动零
给定一个数组 nums
,编写一个函数将所有 0
移动到数组的末尾,同时保持非零元素的相对顺序。
题目本身不难,重要的是思路,遇到这种问题优先考虑双指针法或快慢指针法,本题通过快慢指针法解决
func moveZeroes(nums []int) {// 双指针法,slow <= fast// fast 指向扫描指针slow, fast := 0, 0for ; fast<len(nums); i++ {// 扫描遇到的元素是否为 0if nums[fast] != 0 {// 遇到元素不为0,两种情况// fast = slow, 表示slow 追得上 fast,原因是当前还没有扫描到 0,此时不用做任何操作,// 只需要 slow 跟着fast移动就好// fast > slow, 表示由于出现了0导致slow落后fast,而且slow此时指向fast之前为0的位置,// 此时需要 slow 处的 0 和 fast 处的非 0 交换if fast != slow {nums[slow], nums[fast] = nums[fast], nums[slow]}// 只要出现非0的元素,慢指针 slow 都需要移动slow++}}}
题目4:11.盛最多水的容器
给你 n 个
func climbStairs(n int) int {// 1 -> [(1)] -> 1// 2 -> [(1, 1), (2)] -> 2// 3 -> [(1, 1, 1), (1, 2), (2, 1)] -> climb[1] = climb[2] + climb[1] = 3if n <= 2 {return n}// 存储两阶台阶的结果arr := []int{1, 2}for i:=3; i<=n; i++ {steps := arr[1] + arr[0]arr[0] = arr[1]arr[1] = steps}return arr[1]}
题目4:11.盛最多水的容器
给你 n 个非负整数 a1,a2,...,an,每个数代表坐标中的一个点 (i, ai) 。在坐标内画 n 条垂直线,垂直线 i 的两个端点分别为 (i, ai) 和 (i, 0) 。找出其中的两条线,使得它们与 x 轴共同构成的容器可以容纳最多的水。
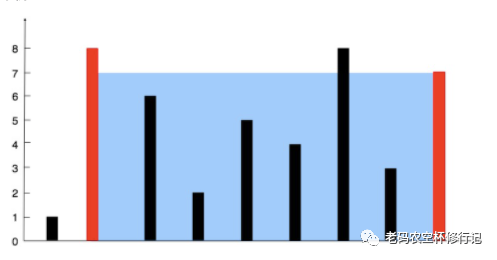
要点分析
柱子高度(也就是数组元素的值,有高有低)不一样 不能倾斜,说明盛水多少有低的柱子决定
func maxArea(height []int) int {size := len(height)// max 保存最大容量// left 容器的做边沿坐标// right 容器的右边沿坐标max, left, right := 0, 0, size - 1// 终止条件,左边沿和有边沿不能重合for left < right{// 计算容器的宽度 和 长度width := right - lefthight := minInt(height[right], height[left])// 面积 tmp = 宽度 * 高度if tmp := width * hight; tmp > max {// 存储最大max = tmp}// 移动边沿低的那一边, 通过两段低的一段// 逐渐逼近,最终得到最优的解if height[left] > height[right] {right--} else {left++}}return max}func minInt(x, y int) int {if x < y {return x}return y}
文章转载自老码农空杯修行记,如果涉嫌侵权,请发送邮件至:contact@modb.pro进行举报,并提供相关证据,一经查实,墨天轮将立刻删除相关内容。






