Fast unfolding of communities in large networks
Journal of Statistical Mechanics Theory and Experiment 2008(10) · April 2008
vincent.blondel@uclouvain.be jean-loup.guillaume@lip6.fr r.lambiotte@imperial.ac.uk
摘要 Abstract
我们提出了一种简单的方法来检测/提取大型网络的社区结构。我们的方法是一种基于模块度优化的启发式方法。在计算时间方面,它表现出优于所有其它已知的社区检测方法。此外,通过所谓的模块度来衡量,检测到的社区的质量非常好。首先通过识别260万客户的比利时移动电话网络中的语言社区以及分析1.18亿个节点和超过10亿个链接的网络图来显示这一点。我们的算法的准确性也在ad-hoc模块化网络上得到验证。 Our method is a heuristic method that is based on modularity optimization. It is shown to outperform all other known community detection method in terms of computation time. Moreover, the quality of the communities detected is very good, as measured by the so-called modularity.
1. 介绍 Introduction
社会,技术和信息系统通常可以用复杂的网络来描述,这些复杂的网络具有结合组织和随机性的互连顶点的拓扑结构。当社交网络服务,移动电话网络或web网络等大型网络的典型规模在数百万/十亿节点,这些规模要求新方法从其结构中检索综合信息。一种有前途的方法在于将网络分解为子单元或社区,这些子单元或社区是高度互连的节点集。识别这些社区至关重要,因为它们可能有助于发现先验未知的功能模块,例如信息网络中的主题或社交网络中的网络社区。此外,所得到的元网络(其节点是社区)可以用于可视化原始网络结构。
社区检测的问题需要将网络划分为密集连接的节点的社区,属于不同社区的节点仅稀疏地连接。已知该优化问题的精确公式在计算上是难以处理的。因此,已经提出了几种算法以合理快速的方式找到相当好的分区。近年来,由于大型网络数据集的可用性增加以及网络对日常生活的影响,这种对快速算法的搜索引起了人们的极大兴趣。可以区分几种类型的社区检测算法:分裂算法检测社区间链接并将其从网络中删除[4,5,6],凝聚算法递归地合并类似的节点/社区[7],优化方法基于最大化目标函数[8,9,10]。
由这些方法产生的分区的质量,通常通过所谓的分区模块度/模块性/模块化(modularity)来测量。分区的模块度是-1和1之间的标量值,它测量社区内链接的密度,与社区之间的链接相比[4,11]。在有权重的网络中,可以定义如下:
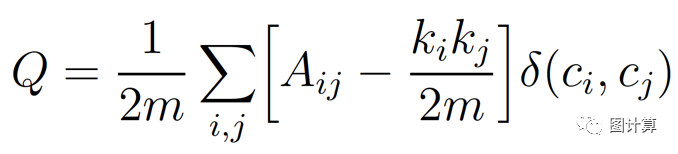
其中:
Aij 表示顶点i和顶点j之间相连的边的权重值(represents the weight of the edge between i and j)。即顶点i指向顶点j的边的权重值,当网络不带权时,此权重可以看做是1;
ki=Sigma(j)Aij 表示附加到顶点i的边的权重之和(is the sum of the weights of the edges attached to vertex i)。即所有指向顶点 i 的边的权重之和,kj同理,当图不带权时,即为顶点i的入度数;
ci 表示顶点i所在的社区编号(is the community to which vertex i is assigned);
Func d(u,v) 函数 表示当u等于v时为1,否则为0(is 1 if u = v and 0 otherwise)。即若顶点i 和顶点j 在同一个社区内,则返回1,否则返回0;
m=1/2 Sigma Aij 表示所有边的权重之和。当图不带权时表示边的总数,充当归一化的作用。
注意:模块度的概念不是Louvain算法/本文首次提出发表,Louvain算法是以优化图模块度Q为目标的一种策略优化实现。
modularity Q的计算公式背后体现了这种思想:社区内部边的边权重总和,减去所有与社区顶点相连的边的权重和;对无向图更好理解,即社区内部边的度数之和,减去社区内节点的总度数。

模块度已被用于比较通过不同方法获得的社区的质量,但也作为优化的目标函数。不幸的是,精确的模块度优化的计算很难,因此在处理大规模图时需要近似算法。
(1)Clauset等人提出了用于优化大型网络模块化的最快近似算法。该方法包括反复合并优化模块度生产的社区。不幸的是,这种贪婪算法可能产生的模块度值明显低于使用例如模拟退火所能找到的值(虽然快速但是可能不够准确)。
(2)此外,[8]中提出的方法倾向于产生包含大部分节点的超级社区,即使在没有重要社区结构的合成网络上也是如此。这种假象还具有显着减慢算法速度并使其不适用于超过一百万个节点的网络的缺点。通过引入技巧来平衡合并社区的大小,从而加快了运行时间,并且可以处理具有几百万个节点的网络,从而避免了这种不希望的影响[16]。
到目前为止,文献中处理的最大图是30739个顶点的蛋白质间相互作用网络[17];一个大型在线零售商网站上出售的约40万个物品的网络[8];日本的一个社交网络系统约有550万用户[16]。这些规模仍然留有相当大的改进空间[18],考虑到截至今日,社交网络服务Facebook拥有约6400万活跃用户,移动网络运营商Vodaphone拥有约2亿客户,谷歌索引数十亿网页。让我们也注意到,在上面列出的大多数大型网络中,有几个自然组织层次 - 社区将自己划分为子社区- 因此需要获得揭示这种层次结构的社区检测方法[19]。
2. 方法 Method
现在介绍我们的Louvain算法,该算法在短时间内找到大型网络的高模块读分区,并为网络展开完整的分层社区结构,从而提供对社区检测的不同分辨率的访问。与所有其他社区检测算法相反,我们的算法所面临的网络大小限制是由于存储容量有限而不是有限的计算时间:在1.18亿个顶点网络中识别社区只需要152分钟[20]。我们的算法被分为两阶段的重复迭代过程。假设我们从N个节点的带权网络/图开始。
(1)首先,我们为网络的每个顶点分配一个不同的社区编号。因此,在这个初始分区中,存在与顶点数一样多的社区。
(2)然后,对于每个顶点i,我们考虑i的邻居顶点j(0或多个),并且我们通过将i从其社区中移除并将其放置在j的社区中来评估将发生的模块度的增益。
(3)接着,仅当该增益为正时,将顶点i放置在增益最大的顶点j所在的社区中(如果有多个j的社区的增益都相等,我们使用破坏规则);如果没有可能获得正收益,顶点i会留在原来的社区。
(4)对所有节点重复并顺序地应用该过程(2)和(3),直到不能实现进一步改进,然后完成第一阶段。
让我们聚焦到一个顶点可能并且经常被多次考虑(评估模块度)的事实。当达到模块度的局部最大值时,即当没有单独的移动可以改善模块度时,该第一阶段停止。还应注意,算法的输出取决于顶点被处理(评估计算模块度)的顺序。几个测试用例的初步结果似乎表明顶点的排序对获得的模块度没有显着影响。但是,处理的顺序会影响计算时间。因此选择适当的顺序值得研究,因为它可以提供良好的启发式以提升计算性能。
算法效率的一部分源于这样的事实:通过将孤立顶点i移动到社区C中获得的模块度增益?DQ可以通过以下方式轻松计算:
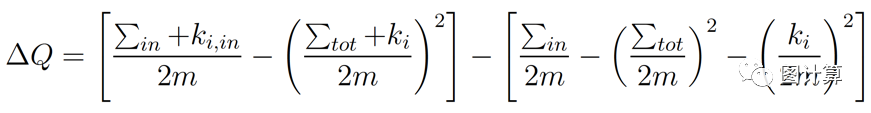
Sigma(in) 表示社区C内部的边的权重之和。 (is the sum of the weights of the links inside C)
Sigma(tot) 表示与社区C内的顶点相连的边的权重之和。(is the sum of the weights of the links incident to nodes in C)
ki=Sigma(j)Aij 表示附加到顶点i的边的权重之和(is the sum of the weights of the links incident to node i)。即所有指向顶点i 的边的权重之和,当图不带权时,即为顶点i的入度数;
ki,in 表示社区C内顶点与顶点i的边的权重之和(is the sum of the weights of the links from i to nodes in C);
m 表示图中所有边的权重之和(is the sum of the weights of all the links in the network);
当我从社区中移除顶点i时,使用类似的表达式来评估模块度的变化。因此,在实践中,算法通过将i从其社区中移除,然后将其移动到邻近社区来评估模块度的变化。
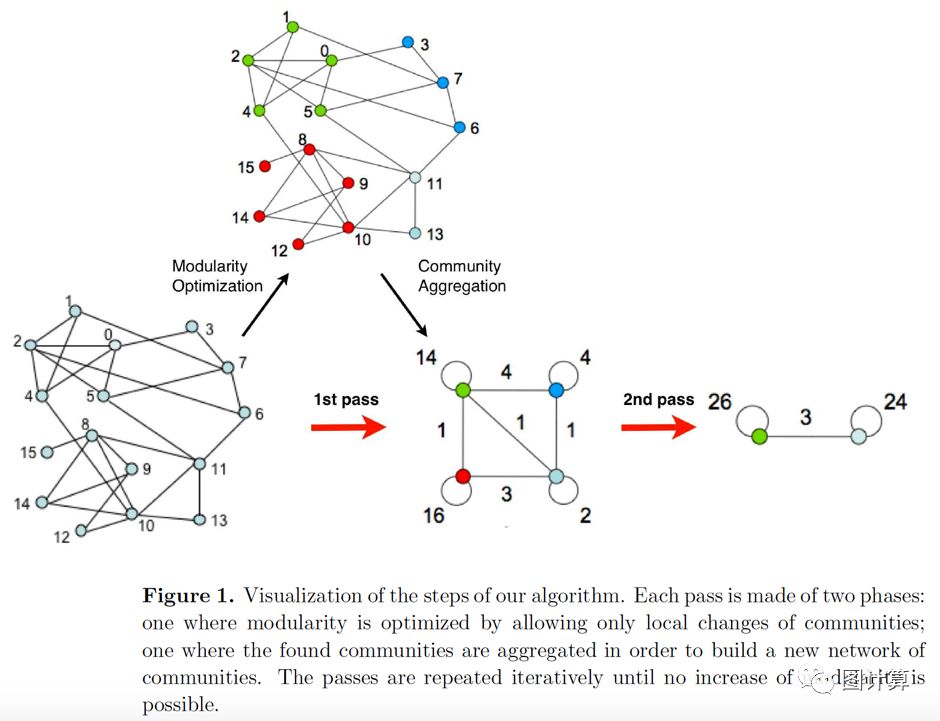
该算法的第二阶段在于构建一个新网络,其新顶点是第一阶段中找到的社区。为此,新顶点(社区)之间边的权重由相应两个社区中顶点之间边权重的总和给出[21]。同一社区内顶点之间的链接导致新网络中此社区的自我循环。一旦完成第二阶段,就可以将算法第一阶段重新应用于,新得到的加权网络并进行迭代。让我们通过“pass”表示这两个阶段的组合。通过构造,元社区的数量在每次pass时减少,因此大部分计算时间花在第一次的pass。迭代过程(参见Figure1),直到没有更多变化并获得最大的模块度。该算法让人想起复杂网络的自相似性[22],并且自然地结合了层次结构的概念,因为社区的社区是在过程中建立的。构造的层次结构的高度由pass次数确定,并且通常是一个小数字,如下面的一些示例所示。
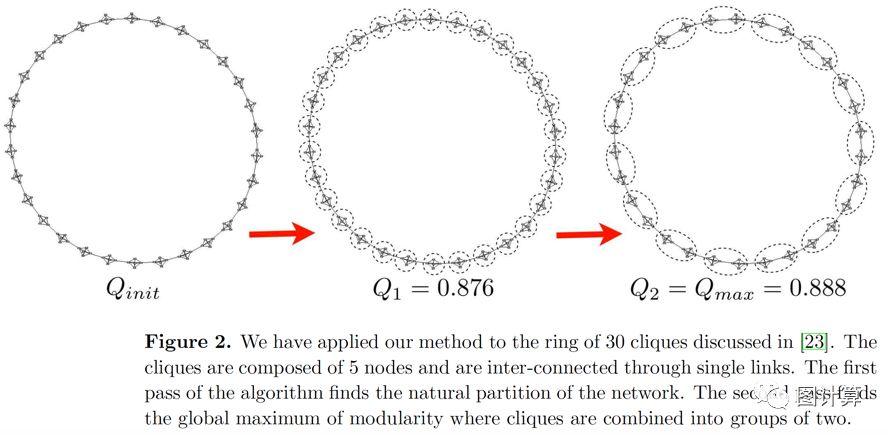
这种简单的算法有几个优点。首先,它的步骤直观且易于实现,是无监督的结果。此外,该算法非常快,即,在大型ad-hoc模块化网络上的计算机模拟表明其复杂性在典型和稀疏数据上是线性的。这是因为使用上述公式可以很容易地计算模块化的潜在增益,并且在几次pass之后社区的数量急剧减少,因此大部分运行时间集中在第一次迭代上。由于我们的算法具有固有的多层次特性,所以模块度的分辨率限制问题似乎也被规避了。实际上,众所周知[23]模块度优化无法识别小于特定规模的社区,从而导致通过纯模块度优化方法检测到的社区的分辨率受到限制。这种观察在我们的案例中只是部分相关,因为我们算法的第一阶段涉及将单个节点从一个社区转移到另一个社区。因此,通过逐个移动顶点合并两个不同社区的概率非常低。在聚合了顶点块之后,这些社区可能在后来的通道中合并。但是,我们的算法将网络分解为不同组织级别的社区。例如,当应用于[23]中提出的clique网络时,派系确实在最终分区中合并,但在第一遍之后它们是不同的(见Figure2)。该结果表明,由我们的算法找到的中间解决方案也可能是有意义的,并且未覆盖的分层结构可以允许最终用户放大网络并以期望的分辨率观察其结构。
3 应用于大规模网络 Applicationto large networks
由下表的结果显示Louvain算法的模块度值明显高于其它算法,而运行时间远低于其它算法,并且可以处理billion级别的超大规模网络。
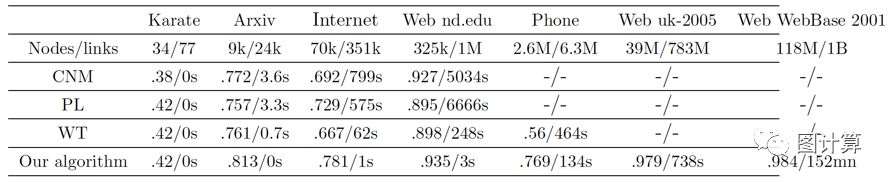
数值结果摘要: 该表给出了Clauset,Newman和Moore [8]的(CNM)算法,Pons和Latapy [7]的(PL)算法,Wakita和Tsurumi [16]的(WT)算法以及我们的Louvain算法在各种大小的网络中进行社区检测的算法性能。对于每个方法/网络,该表显示实现的模块度和计算时间。空单元格对应超过24小时内的计算时间。我们的方法在计算时间和模块度方面表现得更好。值得注意的是,WT为移动电话网络发现的Q值很小。这种糟糕的模块化结果可能源于他们的启发式创建平衡的社区,而我们的方法在这个特定的网络中提供不平衡的社区。
In order to verify the validity of our algorithm, we have applied it on a number of test case networks that are commonly used for efficiency comparison and we have compared it with three other community detection algorithms (see Table 1).
We have also tested the sensitivity of our algorithm by applying it on ad-hoc networks that have a known community structure.
To validate the communities obtained we have also applied our algorithm to a large network constructed from the records of a Belgian mobile phone company.
4. 总结与讨论 Conclusionand discussion
我们引入了一种优化模块度的算法,可以研究前所未有的大规模网络。我们进行的实验方法的局限性是网络在主存储器中的存储而不是计算时间。这种尺度的变化,即从先前方法的大约5百万个顶点到我们的情况下的超过1亿个顶点,开启了激动人心的视角,因为现在可以解开诸如整个国家或互联网的大部分的复杂系统的模块化结构。我们的方法的准确性也已经在ad-hoc模块化网络上进行了测试,并且与其他(慢得多)社区检测方法相比显示出优势。值得注意的是,通过使用一些简单的启发式方法,我们的算法的速度仍然可以大大提高,例如当模块度的增益低于给定阈值时停止算法的第一阶段或者通过移除1度节点(离开)来自原始网络并在社区计算后添加回来。应进一步研究这些启发式算法对网络最终划分的影响,以及算法第一阶段节点排序所起的作用。
参考:
https://arxiv.org/abs/0803.0476v2
https://www.cnblogs.com/fengfenggirl/p/louvain.html
本文内容仅个人观点,如有错误和不足之处还望大家雅正,如果对您有所帮助则是我的荣幸,如需本文相关资料请发邮件到zhangguoqingas@gmail.com或留言!






