看了这么多图计算的文献,好像没有哪篇文章不提PageRank算法的,可见它在图计算研究领域的重要性,下面我们具体了解它。
PageRank算法[1]首次于1998年由斯坦福大学的Sergey Brin和Lawrence Page公开发表于在Computer Networks and ISDN Systems(计算机网络和综合业务数据网系统, 荷兰) 第七届International World Wide Web Conference (WWW)。没错,Sergey Brin和Lawrence Page就是谷歌的创始人,并且PageRank现在依然是Google搜索的核心支撑算法,后台具体应该是运行在谷歌内部的Pregel [2]系统上。Pregel也算是业内首个公认的图计算系统了,属于Distributed In-Memory 类别。此外,我们应该知道谷歌发布研究成果有个特点,那就是所发表的成果一般都是已经在其内部稳定使用多年的,即可靠性很高也颇被各类顶级期刊认可。网络方面一个典型的例子就是Google的TCP拥塞控制算法BBR:Congestion-Based Congestion Control [3],实际上它早已在谷歌B4网络中使用多年了。存储方面一个典型的例子是谷歌文件系统”The Google file system” GFS[4]。

所以PageRank算法出现已经快30年了,网上也有很多关于它的各类资料,而我们不妨先换个角度,从论文上去学习它?原因如下:(1)毕竟那些比较新的知识都是从论文上首先传播的,做为研究生应该改变获取知识的途径,不能再像本科或中学那样了。(2)并且计算机相关的基础课程教材内容很多也都是从无数paper中提炼出来的。后面也会有讨论如何快速阅读计算机相关书籍的文章。(3)往往原文的描述更朴素且容易理解。而如何克服英文阅读障碍后面也会有文章介绍,敬请期待!(4)可以作为后期论文写作的积累。那么今天就跟着我从PageRank做个尝试吧,关于PageRank算法的原文是[1]和[5]。
在[1]中System features有下面这句话
The Google search engine has two important features that help it produce high precision(精度) results. First, it makes use of the link structure of the Web to calculate a quality ranking for each Web page.This ranking is called PageRank and is described in detail in [7]. (文中的[7]就是本文的[5])
在[1]中PageRank: bringing order to the Web
These maps allow rapid(迅速的) calculation of a Webpage’s “PageRank”, an objective measure(度量) of its citation(引用) importance that corresponds(符合,一致) well with people’s subjective(主观) idea of importance. Because of this correspondence(通信,一致,相当), PageRank is an excellent(卓越的,极好的,杰出的) way to prioritize(把事情按优先顺序排好) the results of Web keyword searches.
在[1]中Description of PageRank calculation
Academic(学术的) citation literature(文学,文献,著作) has been applied to the Web, largely by counting citations or backlinks to a given page. This gives some approximation(近似,接近) of a page’s importance or quality. PageRank extendsthis idea by not counting links from all pages equally, and by normalizing by the number of links on a page. PageRank is defined as follows:
We assume page A has pages TI...Tn which point to it (i.e., are citations). The parameter d is a damping(抑制,阻尼,衰减) factor which can be set between 0 and 1. We usually set d to 0.85. There are more details about d in the next section. Also C(A) is defined as the number of links going out of page A. The PageRank of a page A is given as follows:
PR(A) = (1 - d) + d * ( PR(T1)/C(T1) + …. +PR(Tn)/C(Tn) )
Note that the PageRanks form a probability distribution(概率分布) over Web pages, so the sum of all Web pages’ PageRanks will be one.
PageRank or PR(A) can be calculated using a simple iterative(迭代) algorithm, and corresponds to the principal eigenvector(主特征向量) of the normalized(标准化,正规化) link matrix of the Web. Also a PageRank for 26 million Web pages can be computed in a few hours on a medium size workstation.
在[5]中Abstract有下面这句话
This paper describes PageRank, a method for rating Web pages objectively and mechanically(机械地,呆板地,物理上的), effectively measuring the human interest and attention devoted to them.
在[5]中关于PageRank的描述
In order to measure the relative importance of web pages, we propose PageRank, a method for computing a ranking for every web page based on the graph of the web. PageRank has applications in search, browsing, and traffic estimation.
Link Structure of the Web
Every page has some number of forward links(outedges) and backlinks (inedges) (see Figure 1). We can never know whether we have found all the backlinks of a particular page but if we have downloaded it, we know all of its forward links at that time.
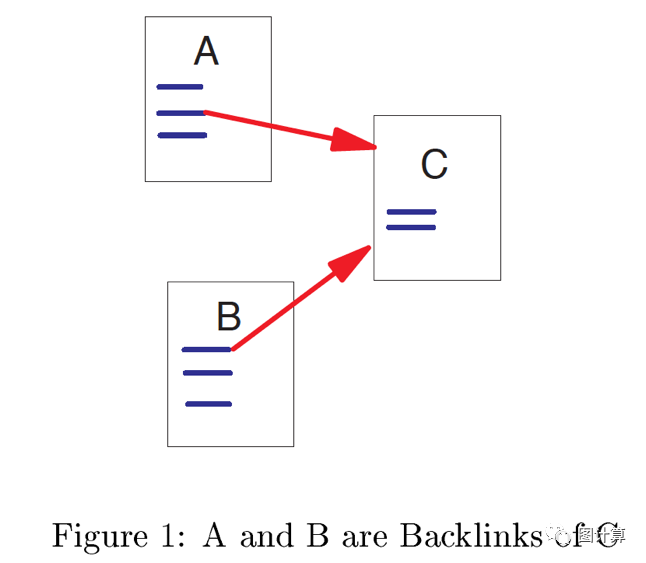
Generally, highly linked pages are more “important” than pages with few links. PageRank provides a more sophisticated(复杂的,精致的,富有经验的) method fordoing citation counting. PageRank is an attempt to see how good an approximation(近似法,近似值) to “importance" can be obtained(获得) just from the link structure.
下面则是PageRank比较核心的描述了
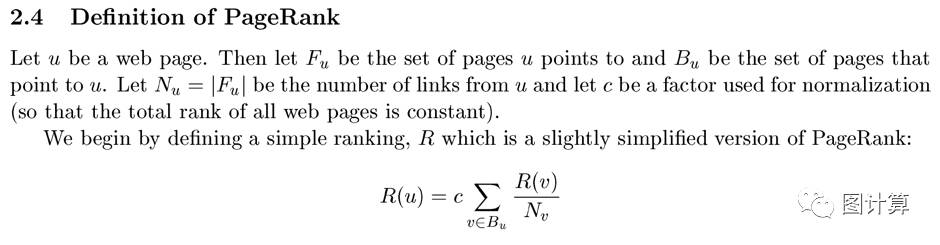
Based on the discussion above, we give the following intuitive(直觉的,凭直觉获知的) description of PageRank: a page has high rank if the sum of the ranks of its backlinks is high. This covers both the case when a page has many backlinks and when a page has a few highly ranked backlinks.
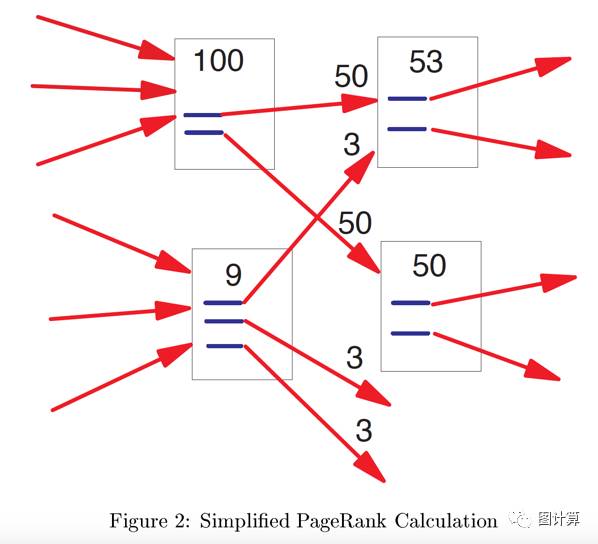
Note that the rank of a page is divided among its forward links evenly to contribute to the ranks of the pages they point to. Note that c < 1 because there are a number of pages with no forward links and their weight is lost from the system. The equation is recursive(递归) but it maybe computed by starting with any set of ranks and iterating(迭代) the computation until it converges(收敛).
后面是使用rank source解决简化版PageRank中rank sink问题的描述。


在GridGraph中是这么描述PageRank算法的
PageRank is a link analysis algorithm that calculates a numerical(数值的) weighting to each vertex in the graph to measure its relative importance among the vertices. The PR value of each vertex is initialized(初始化) to 1. In each iteration, each vertex sends out their contributions to neighbors(邻居), which is the current PR value divided by its out degree. Each vertex sums upthe contributions collected from neighbors and sets it as the new PR value. It converges when the mean difference reaches some threshold1 (阈值,门槛,极限,临界值).
1 Sometimes we run PageRank for certain number ofiterations to analyze performance.
请尽量尝试反复去阅读上面的文献内容来了解PageRank算法,可能的陌生词汇已经给出了中文标注。后面我会写如何用Hadoop运行PageRank算法的文章,届时我会再对PageRank算法用中文做个总结。
[1] Sergey Brin and LawrencePage, The Anatomy of a Large-Scale Hypertextual Web Search Engine. in Proc. 7thIntl. Conf. on the World Wide Web, 1998, 107-117.
[2] MALEWICZ, G., AUSTERN, M. H., BIK, A. J., DEHNERT, J. C., HORN, I., LEISER, N., AND CZAJKOWSKI, G.Pregel: a system for large-scale graph processing. In Proc. SIGMOD (2010).
[3] https://dl.acm.org/citation.cfm?id=3022184&CFID=1001173236&CFTOKEN=34062195 (如果您下载不了,请发邮件到474751729@qq.com)
[4] S. Ghemawat, H. Gobioff,and S.-T. Leung. The Google file system. In Proceedings of the 19th ACMSymposium on Operating Systems Principles (SOSP ’03), Bolton Landing, NY, Oct.2003. ACM.
[5] L. Page, S. Brin, R. Motwani, and T. Winograd. ThePageRank citation ranking: Bringing order to the web. Technical report,Stanford University, 1998.






