key-value数据库bbolt深入分析：B+树

前一篇文章简要介绍了bbolt的背景以及文件头格式。本文继续介绍bbolt的存储格式，主要介绍了bbolt如何利用B+树来组织数据并进行快速查询。本文是此系列的第二篇文章。

B+树存储结构

bbolt内部采用了B+树来构建其索引结构。以前只知道内存中的B+树是什么样子的，这次将直观的看到存储在硬盘文件中的B+树是什么样子的。

众所周知，内存中B+树的节点分为内部节点和叶子节点，只有叶子节点包含数据。bbolt实现的存储在文件中的B+树思路大体相同，但细节处理上与内存中的B+树有诸多不同。

bbolt实现的B+树，每一个节点其实就是一个页面，大小通常就是4K。同样，bbolt实现的B+树只有叶子节点包含数据，内部节点只包含对下一级节点的引用。

叶子节点

首先来看叶子节点长什么样子：

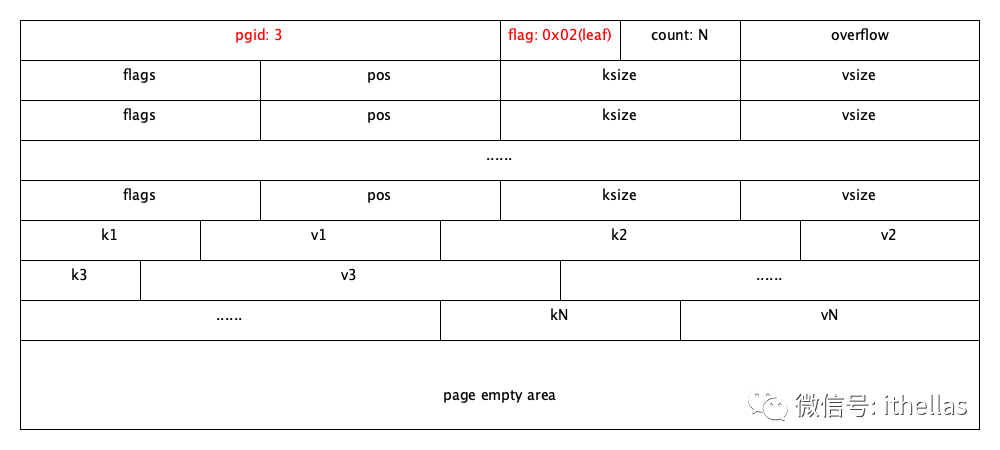
因为一个节点其实就是一个页面，所以每个节点前16个字节就是页面header信息。pgid就是该节点对应的页面ID；flag的值必须是0x02，表示这是一个叶子节点。count的值表示该节点中包含多少个key-value对；如果一个页面无法容纳所有的key-value数据，那么就会分配多个连续的page，这时第一个page header中的overflow就表示后面还有几个page来保存当前节点的数据。

在实际使用中，当为每个页面设置了适当的填充率(例如80%)，一般不会出现一个节点对应多个页面的情况。换句话说，通常情况下，一个节点只对应一个页面。

page header之后，就是page element信息。bbolt为每一个key-value对分配一个leafPageElement结构体，会保存在文件中。注意，leafPageElement并不包含真实的数key-value数据，它只是一些辅助信息，其中flags是标志信息，通常为0，后面会讲到不为0的场景。ksize和vsize分别是key和value的长度，单位是字节。pos是key-value数据的真实存储位置相对于该leafPageElement的偏移。

type leafPageElement struct {
  flags uint32
  pos   uint32
  ksize uint32
  vsize uint32
}

当前节点的所有leafPageElement会保存在连续的空间内。紧接其后的就是真实的key-value数据了。如果页面后面还有剩余空间，那就只能浪费了，别的节点无法利用。

这里要注意一点，一个节点内的所有key-value数据是按key升序排列的。因为对于bbolt来说，所有的key、value都是[]byte，所以是用bytes.Compare来比较key的大小。

内部节点

内部节点的存储结构与叶子节点稍有不同。首先是page header中的flag值不同，对于内部节点，flag的值是0x01。

const branchPageFlag   = 0x01

其次，内部节点只包含有key数据集合，没有value。每一个key是其指向的下一级节点的第一个key值(这就意味着其所指向的下一级节点中的所有key值都大于或等于该key)。内部节点为每一个key分配一个branchPageElement结构体，也会保存在文件中。

type branchPageElement struct {
  pos   uint32
  ksize uint32
  pgid  pgid
}

ksize是其对应的key的长度，单位为字节。pgid是其所指向的下一级节点所在的页面ID。pos是key的真实存储位置相对于该branchPageElement结构体的偏移。

当前节点的所有branchPageElement会保存在连续的空间内。紧接其后的就是真实的key数据了。同样，如果页面后面还有剩余空间，那就只能浪费了，别的节点无法利用。

对于每一个内部节点，其包含的所有key也是按升序排列的，与叶子节点相同。

利用B+树查询

因为不管叶子节点还是内部节点，包含的key都是按升序排列的，所以查询某个key就非常方便。

查询某个key时，会从根节点一路查询到某个叶子节点。在某个节点内(不管是内部节点还是叶子节点)查询时，采用的算法是二分搜索。其实使用的就是golang自带的sort.Search来查询（如下），该算法一目了然，就不啰嗦了。

func Search(n int, f func(int) bool) int {
  // Define f(-1) == false and f(n) == true.
  // Invariant: f(i-1) == false, f(j) == true.
  i, j := 0, n
  for i < j {
    h := int(uint(i+j) >> 1) // avoid overflow when computing h
    // i ≤ h < j
    if !f(h) {
      i = h + 1 // preserves f(i-1) == false
    } else {
      j = h // preserves f(j) == true
    }
  }
  // i == j, f(i-1) == false, and f(j) (= f(i)) == true  =>  answer is i.
  return i
}

对于内部节点n，找到满足下列条件的索引i，然后继续搜索n[i]所指向的下一级节点。

n[i] <= key < n[i+1]

不断重复这个搜索过程，直到到达叶子节点，最终找到目标key为止。

--END--

相关文章

key-value数据库bbolt深入分析：简介、文件头格式