在上篇《二叉树》中已经详细讲解了二叉树及二叉树的一个例子。今天我们来讲二叉树的另一个重要的应用场景,就是在查找中的使用。
假设树中的每个节点存储一项数据。在我们的例子中,虽然任意复杂的项在Java中都容易处理,但为简单起见还是假设他们是整数。假设所有的项都是互异的。
使二叉树称为二叉查找树的性质是,对于树中的每个节点 X,它的左子树中所有项的值小于X中的项,而它的右子树中所有项的值大于X中的项。注意,这意味着该树所有的元素可以用某种一致的方式排序。
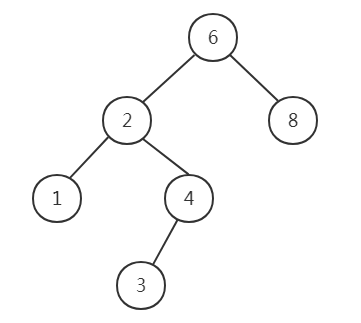
二叉查找树要求所有的项都能排序。要实现这样一个的类,我们需要提供一个interface(接口)来表示这个性质。这个接口就是Comparable,该接口告诉我们,树中的两项总可以使用compareTo方法进行比较。由此,我们能够确定所有其他可能的关系。特别是我们不适用equals方法,而是根据两项相等当且仅当compareTo方法返回0来判断相等。二叉树节点实现如下:
private static class BinaryNode<AnyType>{BinaryNode(AnyType element){this(element, null, null);}BinaryNode(AnyType element, BinaryNode<AnyType> lt, BinaryNode<AnyType> rt){this.element = element;left = lt;right = rt;}AnyType element; //节点数据BinaryNode<AnyType> left; //左节点BinaryNode<AnyType> right; //右节点}
接下来,我们来写一下BinarySearchTree类架构,其中唯一的数据域是对根节点的引用,这个引用对于空树来说是null。对于一个二叉查找树,我们需要有以下几个功能:
查询二叉树中是否包含某个指定节点
查询最小节点
查询最大节点
插入新的节点,生成新的树
删除指定节点,生成新的树
打印树
public class BinarySearchTree<AnyType extends Comparable<? super AnyType>> {private static class BinaryNode<AnyType> {//此处代码和上面代码一致}private BinaryNode<AnyType> root;public BinarySearchTree() {this. root = null;}public void makeEmpty() {this. root = null;}public boolean isEmpty() {return this.root == null;}public boolean contains(AnyType x) {return contains(x, root);}public AnyType findMin() {if(isEmpty())throw new UnderflowException();return findMin(root).element;}public AnyType findMax() {if(isEmpty())throw new UnderflowException();return findMax(root).element;}public void insert(AnyType x) {root = insert(x, root);}public void remove(AnyType x) {root = remove(x, root);}public void printTree() {printTree(this.root);}private boolean contains(AnyType x, BinaryNode<AnyType> t) {//具体实现后面讲解}private BinaryNode<AnyType> findMin(BinaryNode<AnyType> t) {//具体实现后面讲解}private BinaryNode<AnyType> findMax(BinaryNode<AnyType> t) {//具体实现后面讲解}private BinaryNode<AnyType> insert(AnyType x, BinaryNode<AnyType> t) {//具体实现后面讲解}private BinaryNode<AnyType> remove(AnyType x, BinaryNode<AnyType> t) {//具体实现后面讲解}private void printTree(BinaryNode<AnyType> t) {//具体实现后面讲解}}
contains方法
如果在树T中含有项X的接口,name这个操作需要返回true;如果这样的节点不存在,则返回false。
如果T是空集,则返回false,否则,如果存储在T处的项是X,那么可以返回true。否则,我们对树下的左子树或右子树进行一次递归调用,这依赖于X与存储在T中的项的关系。
private boolean contains(AnyType x, BinaryNode<AnyType> t) {if(t == null)return false;int compareResult = x.compareTo(t.element)'if(compareResult < 0) {return contains(x, t.left);} else if (compareResult > 0) {return contains(x, t.right);}return true;}
findMin 方法和findMax 方法
这两个方法分别返回树中包含最小元和最大元的节点的引用。为执行findMin,从根开始并且只要有左儿子就向左进行。终止点就是最小的元素。findMax方法,除分支朝向向右儿子外,其余过程与findMin一致。
public BinaryNode<AnyType> findMin(BinaryNode<AnyType> t) {if(t == null) {reuturn null;} else if (t.left == null) {return t;}return find(t.left);}public BinaryNode<AnyType> findMax(BinaryNode<AnyType> t) {if(t != null) {while(t.right != null) {t = t.right;}return t;}}
insert 方法
为了将X插入到树T中,我们可以沿着树查找,如果找到X,就什么都不做或者执行一些更新。否则将X插入到遍历的路径上的最后一点上。
private BinaryNode<AnyType> insert(AnyType x, BinaryNode<AnyType> t){if(t == null)return new BinaryNode<>(x, null, null);int compareResult = x.compareTo(t.element);if(compareResult < 0){t.left = insert(x, t.left);} else if () {t.right = insert(x. t.right);} else {//重复,做一些更新操作}return t;}
remove 方法
正如许多数据结构一样,最困难的操作是remove(删除)。一旦我们发现要被删除的节点,就需要考虑以下几种可能的情况:
如果节点是一个叶子节点,那么它可以被立即删除。
如果节点有一个儿子,则该节点的子节点需要在父节点删除后调整自己的链。
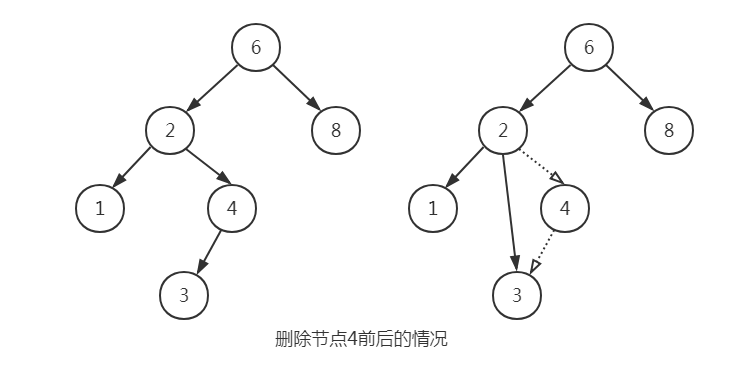
如果节点有两个儿子,一般的删除策略是用其右子树的最小的数据代替该节点的数据并递归的删除那个节点。因为右子树中的最小的节点不可能有左儿子,所以第二次remove要容易。
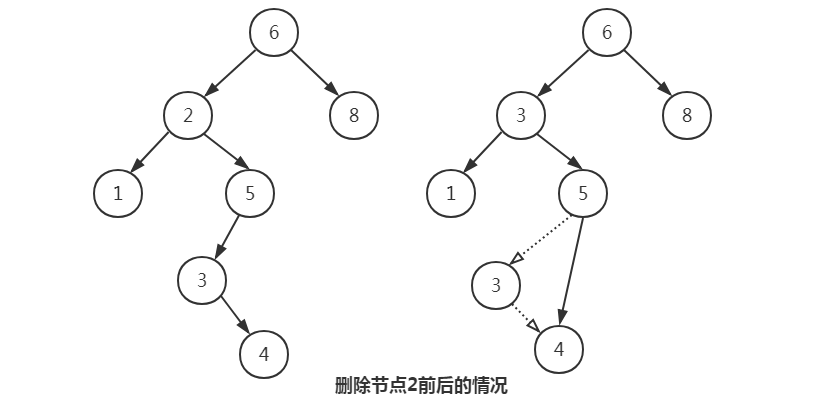
private BinaryNode<AnyType> remove(AnyType x, BinaryNode<AnyType> t) {if(t == null)return t;int compareResult = x.compareTo(t.element);if(compareResult < 0) {t.left = remove(x, t.left);} else if (compareResult > 0) {t.right = remove(x, t.right);} else if (t.left != null && t.right != null) {t.element = findMin(t.right).element;t.right = remove(t.element, t.right);} else {t = ( t.left != null) ? t.left : t.right;}return t;}
print 方法
public void printTree() {if(isEmpty()) {System.out.println("Empty tree");} else {printTree(root);}}private void printTree(BinaryNode<AnyType> t) {if(t != null) {print(t.left);System.out.println(t.element);print(t.right);}}
从上面我们写的代码,我们可以发现删除的效率并不高,因为它沿着该树进行两趟搜索以查找和删除右子树中最小的节点。通过写一个特殊的removeMin方法可以提高删除效率。
如果删除次数不多,通常使用的策略是懒惰删除,就是说当一个元素要被删除时,它仍然留在树中,而只是被标记为删除。这特别是在有重复项时很常用,因为此时记录出现频率数的域可以减1.如果树中的实际节点数和“被删除”的节点数相同,那么树的深度预计只上升一个小的常数,因此,存在一个与懒惰删除相关的非常小的时间损耗。还有一点就是,如果被删除的项是重新插入的,那么分配一个新单元的开销就避免了。
点个“好看”支持一下鸭
点鸭点鸭点鸭
↓↓↓






