模拟退火算法原理
模拟退火算法来源于固体退火原理,在数学建模中经常用到,其基本原理将固体加温至充分高,再让其徐徐冷却,加温时,固体内部粒子随温升变为无序状,内能增大,而徐徐冷却时粒子渐趋有序,在每个温度都达到平衡态,最后在常温时达到基态,内能减为最小。根据Metropolis准则,粒子在温度T时趋于平衡的概率为e(-ΔE/(kT)),其中E为温度T时的内能,ΔE为其改变量,k为Boltzmann常数。用固体退火模拟组合优化问题,将内能E模拟为目标函数值f,温度T演化成控制参数t,即得到解组合优化问题的模拟退火算法:由初始解i和控制参数初值t开始,对当前解重复“产生新解→计算目标函数差→接受或舍弃”的迭代,并逐步衰减t值,算法终止时的当前解即为所得近似最优解,这是基于蒙特卡罗迭代求解法的一种启发式随机搜索过程。退火过程由冷却进度表(Cooling Schedule)控制,包括控制参数的初值t及其衰减因子Δt、每个t值时的迭代次数L和停止条件S。
模拟退火算法的模型
1.模拟退火算法可以分解为解空间、目标函数和初始解三部分。
2.模拟退火的基本思想:
(1) 初始化:初始温度T(充分大),初始解状态S(是算法迭代的起点),每个T值的迭代次数L
(2) 对k=1, …, L做第(3)至第6步:
(3) 产生新解S′
(4) 计算增量ΔT=C(S′)-C(S),其中C(S)为评价函数
(5) 若ΔT<0则接受S′作为新的当前解,否则以概率exp(-ΔT/T)接受S′作为新的当前解.
(6) 如果满足终止条件则输出当前解作为最优解,结束程序。
终止条件通常取为连续若干个新解都没有被接受时终止算法。
(7) T逐渐减少,且T->0,然后转第2步。
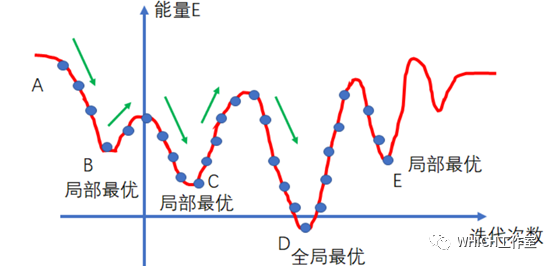
模拟退火算法的步骤
模拟退火算法新解的产生和接受可分为如下四个步骤:
第一步是由一个产生函数从当前解产生一个位于解空间的新解;为便于后续的计算和接受,减少算法耗时,通常选择由当前新解经过简单地变换即可产生新解的方法,如对构成新解的全部或部分元素进行置换、互换等,注意到产生新解的变换方法决定了当前新解的邻域结构,因而对冷却进度表的选取有一定的影响。
第二步是计算与新解所对应的目标函数差。因为目标函数差仅由变换部分产生,所以目标函数差的计算最好按增量计算。事实表明,对大多数应用而言,这是计算目标函数差的最快方法。
第三步是判断新解是否被接受,判断的依据是一个接受准则,最常用的接受准则是Metropolis准则: 若ΔT<0则接受S′作为新的当前解S,否则以概率exp(-ΔT/T)接受S′作为新的当前解S。
第四步是当新解被确定接受时,用新解代替当前解,这只需将当前解中对应于产生新解时的变换部分予以实现,同时修正目标函数值即可。此时,当前解实现了一次迭代。可在此基础上开始下一轮试验。而当新解被判定为舍弃时,则在原当前解的基础上继续下一轮试验。
模拟退火算法与初始值无关,算法求得的解与初始解状态S(是算法迭代的起点)无关;模拟退火算法具有渐近收敛性,已在理论上被证明是一种以概率l 收敛于全局最优解的全局优化算法;模拟退火算法具有并行性。
代码
导入需要的库
from random import*
import numpy as np
from math import*
from matplotlib import pyplot as plt
import sys
初始化城市的坐标并构建距离矩阵
file_name = sys.argv[1] if len(sys.argv) > 1 else 'data/data1.csv'
citys = np.loadtxt(file_name, delimiter=',')
number_of_citys = citys.shape[0]
print(number_of_citys)
citys = np.array(citys)
#由城市坐标计算距离矩阵
distance = np.zeros((number_of_citys,number_of_citys))
for i in range(number_of_citys):
for j in range(number_of_citys):
distance[i][j] = sqrt((citys[i][0]-citys[j][0])**2+(citys[i][1]-citys[j][1])**2)
初始化参数
#初始化参数
iteration1 = 2000 #外循环迭代次数
T0 = 100000 #初始温度,取大些
Tf = 1 #截止温度,可以不用
alpha = 0.95 #温度更新因子
iteration2 = 10 #内循环迭代次数
fbest = 0 #最佳距离
初始化解
#初始化初解
x = []
for i in range(number_of_citys):
x.append(i)
np.random.shuffle(x)
x = np.array(x)
for j in range(len(x) - 1):
fbest = fbest + distance[x[j]][x[j + 1]]
fbest = fbest + distance[x[-1]][x[0]]
xbest = x.copy()
f_now = fbest
x_now = xbest.copy()
这里的x_now和f_now是SA在运行过程中的当前解,但这个解不一定就是历史最优解,因此我们还设置了f_best和x_best用于记录历史最优解。
主循环和内部循环
主循环就是降温过程,内部循环就是在每一个温度下让算法达到平衡点。
for i in range(iteration1):
for k in range(iteration2):
#生成新解
x1 = [0 for q in range(number_of_citys)]
n1,n2 = randint(0,number_of_citys-1),randint(0,number_of_citys-1)
n = [n1,n2]
n.sort()
n1,n2 = n
#n1为0单独写
if n1 > 0:
x1[0:n1] = x_now[0:n1]
x1[n1:n2+1] = x_now[n2:n1-1:-1]
x1[n2+1:number_of_citys] = x_now[n2+1:number_of_citys]
else:
x1[0:n1] = x_now[0:n1]
x1[n1:n2+1] = x_now[n2::-1]
x1[n2+1:number_of_citys] = x_now[n2+1:number_of_citys]
s = 0;
for j in range(len(x1) - 1):
s = s + distance[x1[j]][x1[j + 1]]
s = s + distance[x1[-1]][x1[0]]
#判断是否更新解
if s <= f_now:
f_now = s
x_now = x1.copy()
if s > f_now:
deltaf = s - f_now
if random() < exp(-deltaf/T0):
f_now = s
x_now = x1.copy()
if s < fbest:
fbest = s
xbest = x1.copy()
温度更新
T0 = alpha * T0 #更新温度
打印最佳路线和最佳距离
#打印最佳路线和最佳距离
print(xbest)
print(fbest)
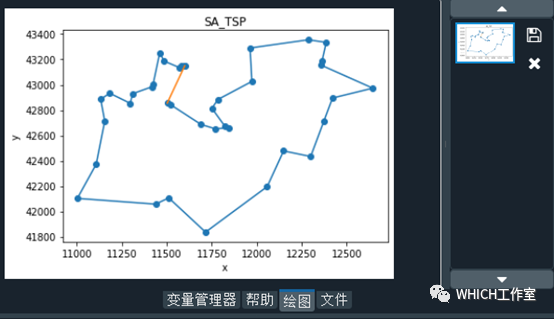
得到可视化结果
代码和数据均已上传到百度网盘
链接:https://pan.baidu.com/s/1eLQ3N0u_TUKfx3yyO6aBYQ
提取码:usix






