遗传算法Python实战 005.图着色问题

写在前面的话

着色图算法是GIS制图学里面的一个经典算法，它可以让你用尽量少的颜色使所有（相邻）的图斑的颜色都是唯一的，最经典的研究就是号称“世界近代三大数学难题之一”的四色定理

四色定理

——以下内容，部分来自百度。

四色问题又称四色猜想、四色定理，是世界近代三大数学难题之一。地图四色定理（Four color theorem）最先是由一位叫古德里（Francis Guthrie）的英国大学生提出来的。。

四色问题的内容是“任何一张地图只用四种颜色就能使具有共同边界的国家着上不同的颜色。”也就是说在不引起混淆的情况下一张地图只需四种颜色来标记就行。比如下面这个中国行政区划图，我们可以看见，任意两个相邻的区域，颜色都完全不一样，而且整个区域仅用四种颜色就足够了。

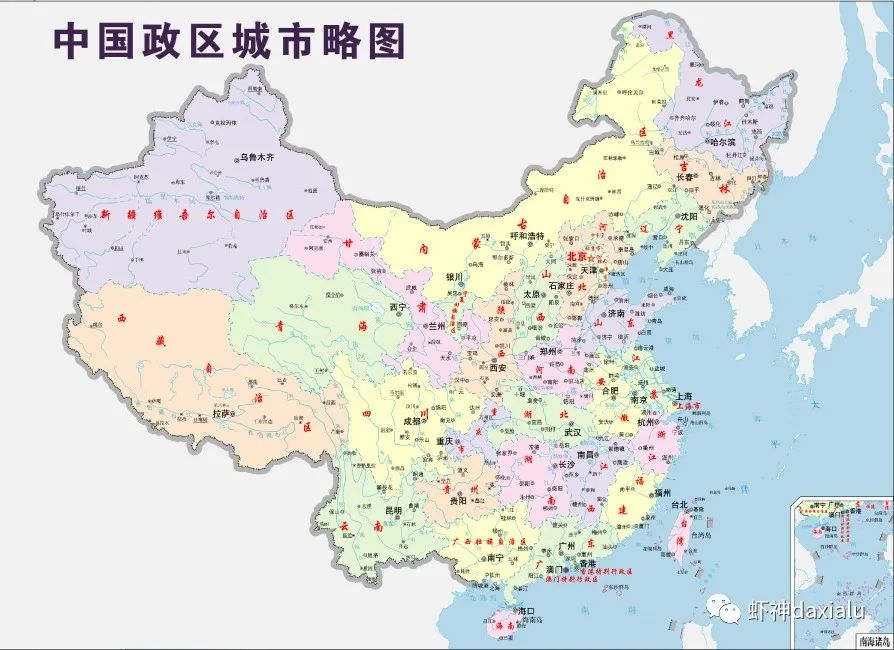
用数学语言表示即“将平面任意地细分为不相重叠的区域，每一个区域总可以用1234这四个数字之一来标记而不会使相邻的两个区域得到相同的数字。”这里所指的相邻区域是指有一整段边界是公共的。如果两个区域只相遇于一点或有限多点就不叫相邻的。因为用相同的颜色给它们着色不会引起混淆。

关于四色问题的各种内容，大家请自行阅读相关材料，我这里就不做农夫山泉了（我们不生产水，我们只是大自然的搬运工……）

进入算法部分

比如我们需要给一份地图上色——就拿美国地图来吧（后面会有中国地图的例子，稍安勿躁）。如果仅仅是考虑物理问题（也就是不考虑视觉上是否合理（好看？），只考虑每个相邻的州的颜色都不一样）那么我们就可以不考虑颜色配比，仅考虑是否符合规则就行。

从逻辑上看，算法实际上很简单：

• 用四种状态来表示四种颜色。

• 从任何一个点开始，先随机给予一种状态。

• 然后在与它相邻的部分，给予一种其他的状态。

• 类推，直到所有的部分都被赋予了一个与自身完全不同的状态为止。

那么，最关键的，就是要定义两个图斑是否相邻——这就是我们做GIS最擅长空间权重矩阵了，推荐大家使用geoda来制作空间权重矩阵——这是另外一个问题了，本系列仅说明算法问题，所以大家可以用我提供好的空间权重矩阵，这里提供CSV格式的。

格式如下（以逗号分隔）：

AL,FL;GA;MS;TN
AR,LA;MO;MS;OK;TN;TX
AZ,CA;NM;NV;UT
……

第一列是当前州的唯一值(英文简写)，第二列是与这个州相邻的所有州（每个州之间用分号分隔开），比如第一行

AL,FL;GA;MS;TN

就表示：阿拉巴马州（AL），临近州（接壤的州）有：佛罗里达州（FL）、佐治亚州（GA）、密西西比州（MS）和田纳西州（TN）。

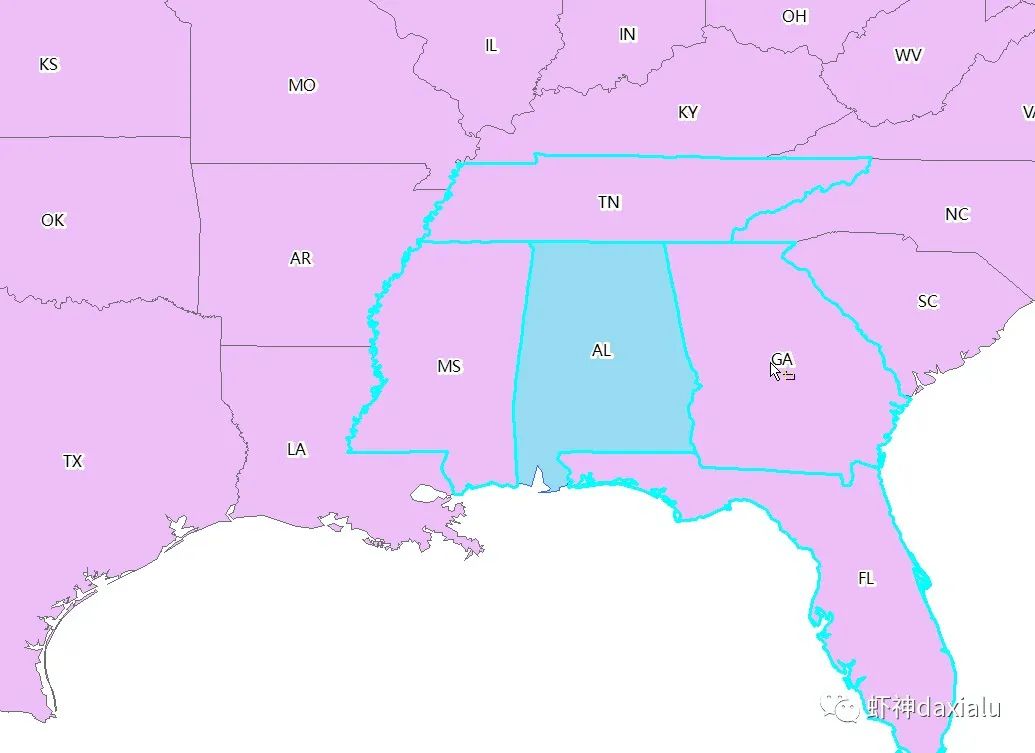
首先，定义一个类，用来承载规则，类的定义如下：

class Rule:
    def __init__(self, node, adjacent):
        if node < adjacent:
            node, adjacent = adjacent, node
        self.Node = node
        self.Adjacent = adjacent

    def __eq__(self, other):
        return self.Node == other.Node and self.Adjacent == other.Adjacent

    def __hash__(self):
        return hash(self.Node) * 397 ^ hash(self.Adjacent)

    def __str__(self):
        return self.Node + " -> " + self.Adjacent

    def IsValid(self, genes, nodeIndexLookup):
        index = nodeIndexLookup[self.Node]
        adjacentNodeIndex = nodeIndexLookup[self.Adjacent]
        return genes[index] != genes[adjacentNodeIndex]

规则类，里面有两个成员变量，分别是当前州和相邻州，注意，在构造函数里面，有个比较的过程，保证了所有的州的顺序都是一样的，比如AL:GA，下一轮输入GA：AL的时候，前后顺序会自动调换过来，依然是AL:GA，保证不会出现重复倚赖的关系。

里面除去四个内置方法里面，就一个功能函数IsValid，这个功能函数的唯一作用就是在选择基因进行进化的时候，判断这个基因是否符合规则——唯一的规则就是你选定的基因（颜色）是不是与相邻的要素是一样的，如果不一样，则有效。

当然，出了构造函数以外，还重构设计了三个内置内，其中：

#函数的作用是判断两个规则是否相等
#相等的规则是是当前的图斑和相邻图斑都相等的时候，认为两个对象就是相等的。
__eq__

#函数主要是用于构造对象的hash值，hash值可以看成是一种数字签名，代表唯一的对象
#如果需要把这个对象当成dict里面的key来用的话，就需要有一个hash值
#这里自己构建一个__hash__方法，用来构建hash值
#（学过数据结构的同学就不用解释了，自己回去看hashmap的原理）。
__hash__

#该函数类似于Java里面的toString
# 当你对这个对象调用print方法的时候，会默认调用这个方法进行输出。
__str__

然后下面出场的就是我们遗传算法的的经典类和经典方法了，这次就不解释了，看以往的文章去：(我都觉得贴代码出来算是水篇幅了)

class Chromosome:
    def __init__(self, genes, fitness):
        self.Genes = genes
        self.Fitness = fitness
        
def mutate(parent,geneSet,size):
    childGenes = parent.Genes[:]
    index = random.randrange(0, len(parent.Genes))
    newGene, alternate = random.sample(geneSet, 2)
    childGenes[index] = alternate if newGene == childGenes[index] else newGene
    fitness = get_fitness(childGenes,rules,size)
    return Chromosome(childGenes, fitness)

然后是一个显示函数，主要用来显示由基因组成的个体信息，当然你也可以直接把整个list直接打印出来也行：

def display(candidate, startTime):
    timeDiff = datetime.datetime.now() - startTime
    print("{0}\t{1}\t{2}".format(
        ''.join(map(str, candidate.Genes)),
            candidate.Fitness,
            str(timeDiff)))

下面是遗传算法里面最重要的方法了——健壮性验证函数：方法非常简单，直接对所有规则进行验证，有效（相邻的没有相同颜色的），就累加1，否则就不进行累加。

def get_fitness(genes, rules, stateIndexLookup):
    rulesThatPass = sum(1 for rule in rules if rule.IsValid(genes, stateIndexLookup))
    return rulesThatPass

下面进入计算环节：首先，因为我们需要读取保存在文本里面的空间关系，所以开始要读取文件，以及构造空间关系：读取csv就不用说了，第二个构建规则的方法，主要是展开空间关系，变成1对1的规则比如：

AL,FL;GA;MS;TN

这一行，就会变成

AL -> FL
AL -> GA
AL -> MS
AL -> TN

四个规则。使用dict的目的，是不会出现重复的结果，然后后面用了个验证，保证所有的规则都最少出现了两次（只算一次有效：比如阿拉巴马州记录了一条和佛罗里达州相邻的记录，那么对应的肯定佛罗里达州也会记录一条和阿拉巴马州一样的规则。

def load_data(localFileName):
    with open(localFileName, mode='r') as infile:
        reader = csv.reader(infile)
        lookup = {row[0]: row[1].split(';') for row in reader if row}
    return lookup
def build_rules(items):
    rulesAdded = {}
    for state, adjacent in items.items():
        for adjacentState in adjacent:
            if adjacentState == '':
                continue
            rule = Rule(state, adjacentState)
            if rule in rulesAdded:
                rulesAdded[rule] += 1
            else:
                rulesAdded[rule] = 1
    for k, v in rulesAdded.items():
        if v != 2:
            print("rule {0} is not bidirectional".format(k))
    return rulesAdded.keys()

然后下面就是运算过程了：先初始化所有的变量，包括读取空间关系文件，初始化构建规则，设置四种颜色：

states = load_data("./adjacent_states.csv")
rules = build_rules(states)
optimalValue = len(rules)
stateIndexLookup = {key: index
        for index, key in enumerate(sorted(states))}
# 下面这两句是定义四种颜色，然后取颜色第一个字母为规则进行赋值
colors = ["Orange", "Yellow", "Green", "Red"]
colorLookup = {color[0]: color for color in colors}
geneset = list(colorLookup.keys())

老规矩的计算方法：

def get_best():
    random.seed()
    startTime = datetime.datetime.now()
    x = [random.choice(geneset) for i in range(len(stateIndexLookup))]
    bestParent = Chromosome(x,get_fitness(x,rules,stateIndexLookup))
    if bestParent.Fitness >= optimalValue:
        return bestParent
    num = 0
    while True:
        num +=1
        child = mutate(bestParent,geneset,stateIndexLookup)
        if bestParent.Fitness > child.Fitness:
            continue
        else:
            display(child,startTime)
            if child.Fitness  >= optimalValue:
                return child
            bestParent = child

执行结果如下：

GGRYRRYOYOGORGGYORRYRYRGYOROOGGGYYGOORGYRGGGOOGGROR	80	0:00:00
GGRYRRYOYOGORGGYORRYRYRGYOROOGGGYYGOOROYRGGGOOGGROR	80	0:00:00
GGRYRRYOYOYORGGYORRYRYRGYOROOGGGYYGOOROYRGGGOOGGROR	82	0:00:00
GGRYRRYOYOYORGGYORRYRYRGYOROOGGGYYGOOROYRGGGOOGGGOR	82	0:00:00.001009
GGRYRYYOYOYORGGYORRYRYRGYOROOGGGYYGOOROYRGGGOOGGGOR	82	0:00:00.001009
……
GRRROYOYOGYROOGYRRORGOOGYYGGRGGGOYYGGRRYOYGYGOOGYYR	106	0:00:00.044880
GRRROYOYOOYROOGYRRORGOOGYYGGRGGGOYYGGRRYOYGYGOOGYYR	106	0:00:00.044880
GRRROYOYOOYRROGYRRORGOOGYYGGRGGGOYYGGRRYOYGYGOOGYYR	106	0:00:00.045878
GRRROYOYOOYRROGYRRGRGOOGYYGGRGGGOYYGGRRYOYGYGOOGYYR	106	0:00:00.045878
GRRROYOYOOYRROGYRRGRGOOGYYGRRGGGOYYGGRRYOYGYGOOGYYR	107	0:00:00.045878

可以看见，最初的时候，只有80条规则符合相邻无重复，随着算法的不断进化，最后107条规则全部完成。

然后我们可以把通过matplotlib绘制出来：

n = sorted(list(states.keys()))
clm = {}
for i in range(len(n)):
    clm[n[i]] = colorLookup[b.Genes[i]]
us = json.load(open("./states.json","r"))
fig = plt.figure(figsize=(14,8)) 
ax = plt.subplot()
for c in us:
    js = json.loads(us[c])
    poly = plt.Polygon(js["rings"][0],ec = '#000000',
                           fc=clm[c], alpha = 0.8)
    ax.add_patch(poly)
       
ax.set_xlim(-178,-66)
ax.set_ylim(18,71)
plt.show()

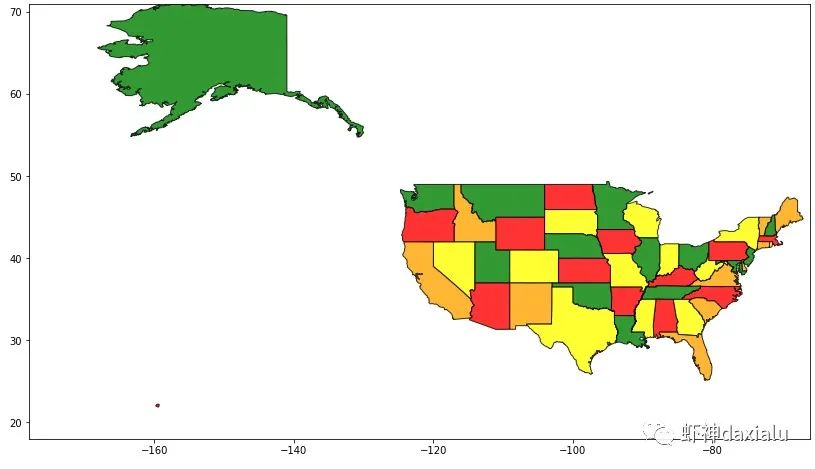
当然，四色问题肯定不止一种结果，而且作为随机原理的遗传算法，每次运行结果也是不一样，下面就是几种不同的解：

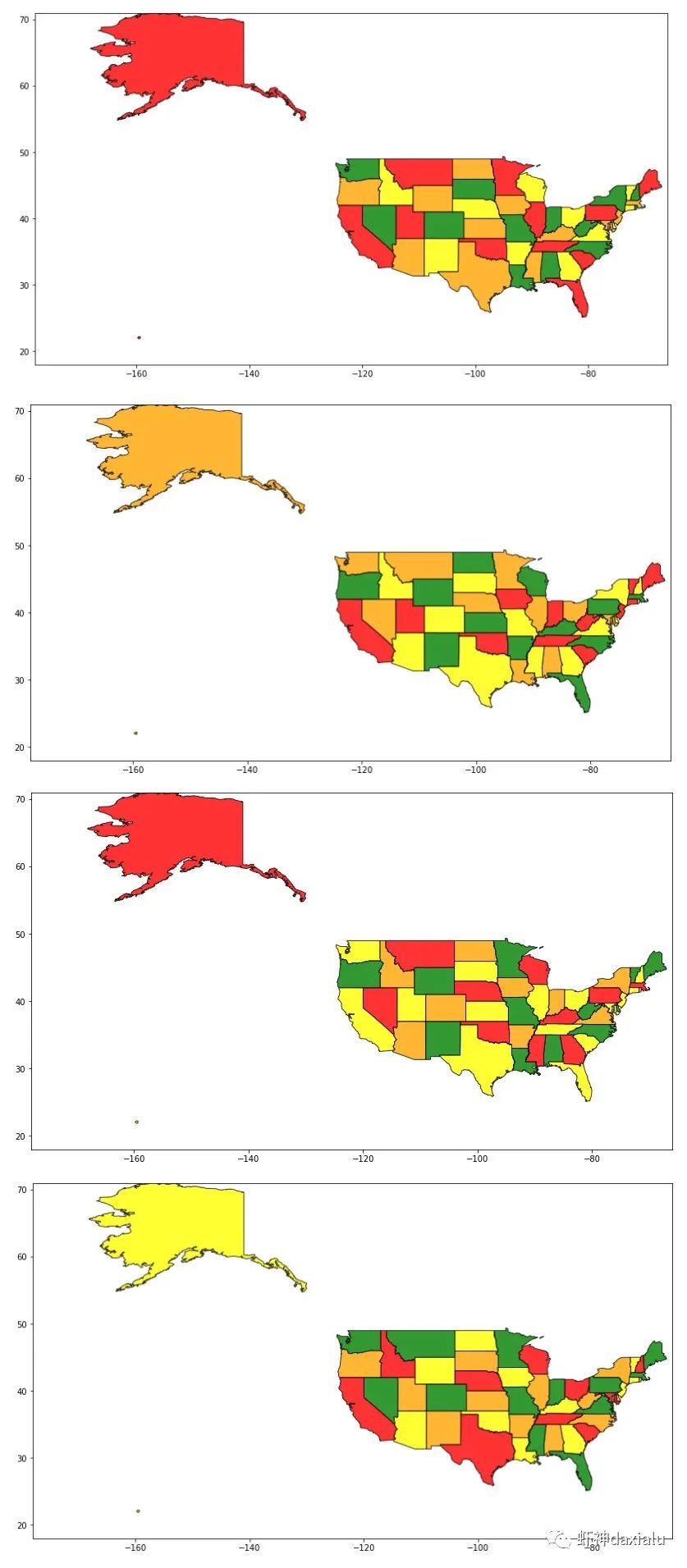
下面我们用中国地图来试试：

代码我就不解释了，大家自己跑。

郑重申明：

本例中使用的中国地图是简化过的版本，仅可用于代码示例和学习，不得用于任何正式的场合，不限于演示、出版、论文等任何公开场合，如果违反该申明出现的任何问题，提供者不承担任何责任。

#代码执行过程略，输出如下：
GOOYROOOGYOGGORROGRGOGORORGRRRGG	52	0:00:00.000999
GOOYROOOGYOGGORROGRGOGORORGRRRYG	52	0:00:00.000999
GOOYROOOGYOGGORROGRGOGORORGRGRYG	54	0:00:00.000999
GOOYROOOGYOGGORROGRGOGORORGRGRYO	54	0:00:00.000999
……
RGYOGOYROGGROYOGORGOOYOGYRRYGOOR	67	0:00:00.054879
RGYOGOYROGGROYOGORGORYOGYRRYGOOR	67	0:00:00.054879
RGYOGOYROGGROYOGORGORYOGYRRYGOOG	67	0:00:00.054879
RGYOGOYROGGROYOGORGORYOGYRRYGOOY	67	0:00:00.054879
RGYOGOYROYGROYOGORGORYOGYRRYGOOY	68	0:00:00.054879

中国三十二个省，只组合出了68个规则，我这里只是进化了886次，就完成了计算，本次执行输出如下：

大家也可以去尝试其他的解。

当然，也去用其他的空间权重矩阵来进行组合，我这里就不多说了。