暑期2021优秀学生的评选已经正式启动了,期待今年闪耀的新星!开源之夏公众号持续欢迎大家分享项目经验,开源心得!
投稿方式:
E-mail :summer@iscas.ac.cn
or 关注公众号,后台回复“投稿”
本期给大家分享的是来自MindSpore社区闫家舜同学的经验分享:保真度算子开发-计算得到量子神经网络演化出的量子态与给定的一个或多个量子态的保真度并能够进行反向传播
保真度计算
在实际的量子计算中,通常会遇到测量问题,即对算符求某量子态下的期望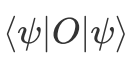 ,例如VQE中需要得到在含参量子态
,例如VQE中需要得到在含参量子态 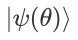 下的哈密顿量的期望
下的哈密顿量的期望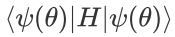 。有时问题需要更一般的测量,这时测量左失不等同于右矢
。有时问题需要更一般的测量,这时测量左失不等同于右矢  ,且被测量算符为非厄米算符
,且被测量算符为非厄米算符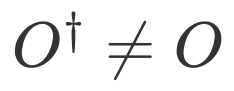 ,例如对非厄米哈密顿量进行测量以得到其非对角元
,例如对非厄米哈密顿量进行测量以得到其非对角元 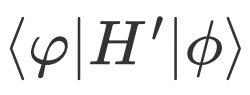 。所以,在mindquantum中提供一个算子实现任意算符的基于任意态矢下的测量是有意义的。如果这个算子可以实现,那么计算量子线路末态和目标态的保真度就变成这个测量算子的一个特例,只需要规定测量右矢为初态
。所以,在mindquantum中提供一个算子实现任意算符的基于任意态矢下的测量是有意义的。如果这个算子可以实现,那么计算量子线路末态和目标态的保真度就变成这个测量算子的一个特例,只需要规定测量右矢为初态 ,被测算符为
,被测算符为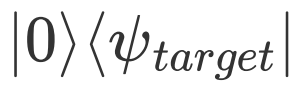 ,测量右矢为演化末态
,测量右矢为演化末态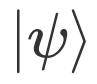 ,既可实现保真度计算
,既可实现保真度计算 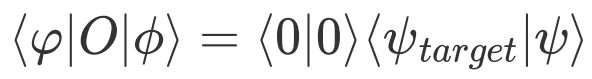 ;或者规定两个测量态矢一个为目标态
;或者规定两个测量态矢一个为目标态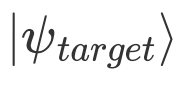 ,一个为线路演化末态
,一个为线路演化末态 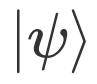 ,被测量算符为单位算符
,被测量算符为单位算符 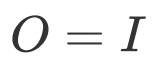 ,同样可以实现
,同样可以实现 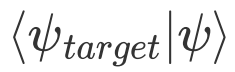 。
。
总的来说,我们实现了一个更普适的算符测量算子,通过规定测量态矢和算符,保真度计算功能可以当做这个算子的特例得以实现。
梯度计算
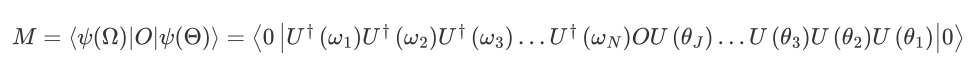
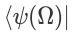 和
和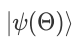 为两个不同的参数化量子线路产生的末态,
为两个不同的参数化量子线路产生的末态,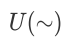 为含参量子门,所以测量结果对某一参数的偏导为
为含参量子门,所以测量结果对某一参数的偏导为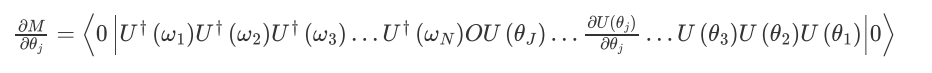
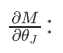
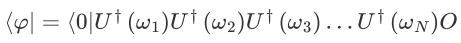 ,赋值右矢
,赋值右矢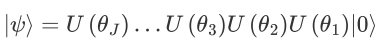
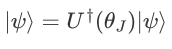
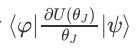
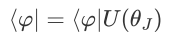
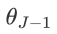 求偏导则可重复(b)~(d),以此类推直至右矢所有参数求导完成。
求偏导则可重复(b)~(d),以此类推直至右矢所有参数求导完成。OneSideGrad(),后端代码为
void OnesideGrad(Projectq<T> &sim_no_grad_side, Projectq<T> &sim_grad_side,const VT<BaseGate<T>> &circ, const VT<BaseGate<T>> &herm_circ,const ParameterResolver<T> &pr, MST<size_t> &p_map, VT<CT<T>> &f_g, bool symmetry = true) {for (size_t j = 0; j < circ.size(); j++) {if ((!herm_circ[j].parameterized_) || (herm_circ[j].params_.requires_grad_parameters_.size() == 0)) {if (herm_circ[j].parameterized_) {sim_no_grad_side.ApplyGate(herm_circ[j], pr, false);sim_grad_side.ApplyGate(herm_circ[j], pr, false);}else {sim_no_grad_side.ApplyGate(herm_circ[j]);sim_grad_side.ApplyGate(herm_circ[j]);}}else {sim_grad_side.ApplyGate(herm_circ[j], pr, false);sim_grad_side.run();Projectq<T> sim_grad_side_tmp = Projectq<T>(1, n_qubits_, sim_grad_side.vec_);sim_grad_side_tmp.ApplyGate(circ[circ.size() - j - 1], pr, true);sim_grad_side_tmp.run();sim_no_grad_side.run();CT<T> gi = 0;if (herm_circ[j].ctrl_qubits_.size() == 0) {gi = ComplexInnerProduct<T, calc_type>(sim_no_grad_side.vec_, sim_grad_side_tmp.vec_, static_cast<Index>(len_));}else {gi = ComplexInnerProductWithControl<T, calc_type>(sim_no_grad_side.vec_, sim_grad_side_tmp.vec_, static_cast<Index>(len_), GetControlMask(herm_circ[j].ctrl_qubits_));}if (symmetry){for (auto &it : herm_circ[j].params_.requires_grad_parameters_){f_g[1 + p_map[it]] -= 2 * herm_circ[j].params_.data_.at(it) * gi;}}else{for (auto &it : herm_circ[j].params_.requires_grad_parameters_){f_g[1 + p_map[it]] -= herm_circ[j].params_.data_.at(it) * gi;}}sim_no_grad_side.ApplyGate(herm_circ[j], pr, false);}}}
VT<VT<CT<T>>> NonHermitianMeasureWithGrad(const VT<Hamiltonian<T>> &hams, const VT<Hamiltonian<T>> &herm_hams,const VT<BaseGate<T>> &left_circ, const VT<BaseGate<T>> &herm_left_circ,const VT<BaseGate<T>> &right_circ, const VT<BaseGate<T>> &herm_right_circ,const ParameterResolver<T> &pr, const VT<std::string> ¶ms_order,size_t mea_threads) {auto n_hams = hams.size();auto n_params = pr.data_.size();bool symmetry = false;MST<size_t> p_map;for (size_t i = 0; i < params_order.size(); i++) {p_map[params_order[i]] = i;}VT<VT<CT<T>>> output(n_hams);Projectq<T> sim = Projectq<T>(1, n_qubits_, vec_);sim.ApplyCircuit(right_circ, pr);Projectq<T> sim2 = Projectq<T>(1, n_qubits_, vec_);sim2.ApplyCircuit(left_circ, pr);#pragma omp parallel for schedule(static) num_threads(mea_threads)for (size_t i = 0; i < n_hams; i++) {VT<CT<T>> f_g(n_params + 1, 0);{Projectq<T> sim_left = Projectq<T>(1, n_qubits_, sim2.vec_);sim_left.ApplyHamiltonian(herm_hams[i]);f_g[0] = ComplexInnerProduct<T, calc_type>(sim.vec_, sim_left.vec_, static_cast<Index>(len_));Projectq<T> sim_right = Projectq<T>(1, n_qubits_, sim.vec_);Projectq::OnesideGrad(sim_left, sim_right, right_circ, herm_right_circ, pr, p_map, f_g, symmetry);}{Projectq<T> sim_right = Projectq<T>(1, n_qubits_, sim.vec_);sim_right.ApplyHamiltonian(hams[i]);f_g[0] = ComplexInnerProduct<T, calc_type>(sim2.vec_, sim_right.vec_, static_cast<Index>(len_));Projectq<T> sim_left = Projectq<T>(1, n_qubits_, sim2.vec_);Projectq::OnesideGrad(sim_right, sim_left, left_circ, herm_left_circ, pr, p_map, f_g, symmetry);}output[i] = f_g;}return output;}
保真度算子实例演示
实例说明
 下的期望值
下的期望值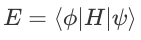
parameter_resolvers.
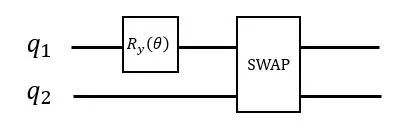
circ1,当旋转Y门
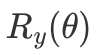 的旋转角为
的旋转角为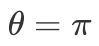 时就变成了一个单比特X门,作用到
时就变成了一个单比特X门,作用到 qubit[0]上使其处于激发态
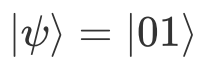 ,再用两比特SWAP门将激发转换到
,再用两比特SWAP门将激发转换到 quibt[1]上,所以线路
circ1得到的末态为
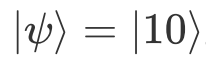 。此时如果
。此时如果 circ2我们不加任何门操作,则测量左失为初态
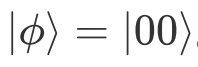 。为了计算保真度,将被测量的哈密顿量定义为
。为了计算保真度,将被测量的哈密顿量定义为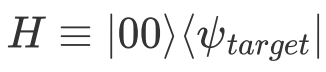 , 则测量得到的期望值变为末态
, 则测量得到的期望值变为末态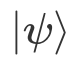 和目标态
和目标态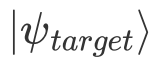
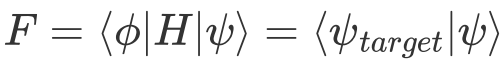 .
.算子测试
from mindquantum import Circuitfrom mindquantum.gate import RY, SWAPGatefrom mindquantum import ParameterResolverimport numpy as npcirc1 = Circuit()circ1 += RY('p1').on(0)circ1 += SWAPGate().on([0, 1])theta = np.pipr = ParameterResolver({'p1': theta})
circ2 = Circuit()
from mindquantum import *from scipy.sparse import csr_matrixzero_state = np.array([1, 0, 0, 0], dtype=complex)target_state = np.array([0, 0, 1, 0], dtype=complex)target_state_ham = zero_state.reshape(4, 1).dot(target_state.reshape(1, 4))hams = Hamiltonian(csr_matrix(target_state_ham))
circ2、哈密顿量hams、线路参数 pr一起传入函数 nonhermitian_measure_with_grad()并接受返回值,保真度
f、梯度g,最后对其打印显示。
from mindquantum.simulator import Simulators = Simulator('projectq', 2)f, g = s.nonhermitian_measure_with_grad(circ2, circ1, [hams], [pr])print('The fidelity is',f)print('The gradient is', np.round(g, 8))
The fidelity is [[1.]]The gradient is [[[0.]]]
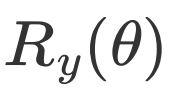 的旋转角度加一个小的偏移
的旋转角度加一个小的偏移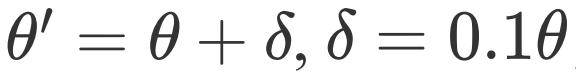 ,这时我们仍以
,这时我们仍以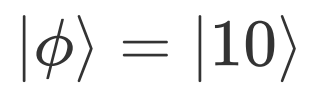 作为目标态,此时得到的结果为
作为目标态,此时得到的结果为delta = 0.1 * thetatheta = theta + deltapr = ParameterResolver({'p1': theta})f, g = s.nonhermitian_measure_with_grad(circ2, circ1, [hams], [pr])print('The fidelity is',f)print('The gradient is', np.round(g, 8))
The fidelity is [[0.98768834]]The gradient is [[[-0.07821723]]]
 ,所以保真度不再为1,梯度不再为零。下面我们对两个值进行验证:首先对量子门
,所以保真度不再为1,梯度不再为零。下面我们对两个值进行验证:首先对量子门 RY门、
SWAP门进行定义
RY = np.array([[np.cos(theta / 2), -np.sin(theta / 2)], [np.sin(theta / 2), np.cos(theta / 2)]],dtype=np.complex128)RY_twoqubits = np.kron(np.array([[1,0], [0,1]]), RY)SWAP = np.array([[1, 0, 0, 0], [0, 0, 1, 0], [0, 1, 0, 0], [0, 0, 0, 1]], dtype=np.complex128)
right_state = np.dot(np.dot(SWAP, RY_twoqubits), np.array([1,0,0,0]).reshape(4,1))target_state = np.array([0,0,1,0])print('The fidelity between the target state and the final state is', np.round(np.dot(target_state, right_state), 8))
The fidelity between the target state and the final state is [0.98768834+0.j]
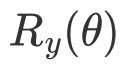 门的对参数
门的对参数 求导的矩阵形式
求导的矩阵形式RY_diff = 0.5 * np.array([[-np.sin(theta / 2), -np.cos(theta / 2)], [np.cos(theta / 2), -np.sin(theta / 2)]], dtype=np.complex128)RY_diff_twoqubits = np.kron(np.array([[1,0], [0,1]]), RY_diff)
right_state_grad = np.array([1,0,0,0]).reshape(4,1)right_state_grad = np.dot(np.dot(SWAP, RY_diff_twoqubits), right_state_grad)print('The gradient is', np.round(np.dot(target_state, right_state_grad), 8))
The gradient is [-0.07821723+0.j]
概述
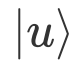 上会出现一个相位
上会出现一个相位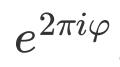 ,现在我们假设U算符的本征值未知,也就是
,现在我们假设U算符的本征值未知,也就是  未知,但是U 算符和本征态
未知,但是U 算符和本征态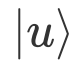 已知,相位估计算法的作用就是对这个相位
已知,相位估计算法的作用就是对这个相位  进行估计。
进行估计。 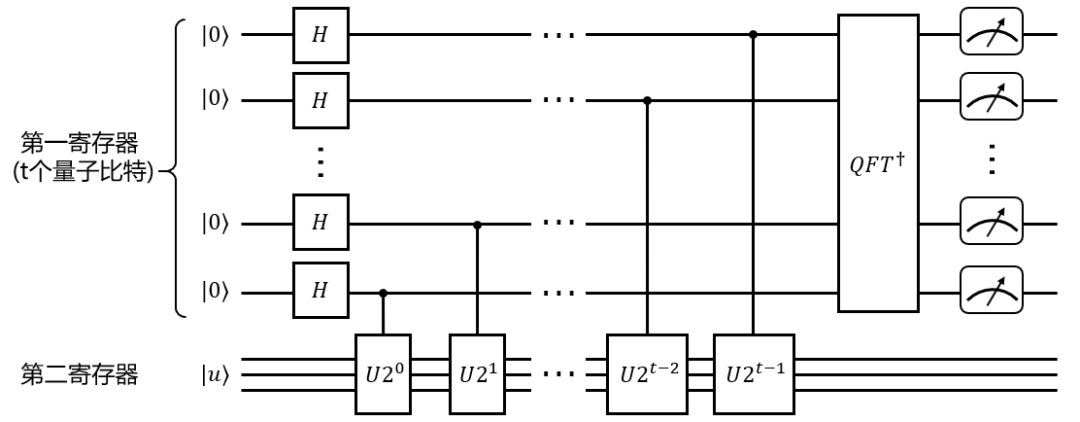
算法解析
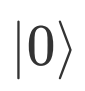
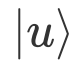 上。相位估计算法主要分为三步:
上。相位估计算法主要分为三步:Hadamard门操作,对第二寄存器连续进行
控制U门操作,其中U门的幂次依次为
 ,控制比特依次为
,控制比特依次为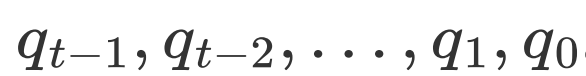 。这时第一寄存器中的态就会变为
。这时第一寄存器中的态就会变为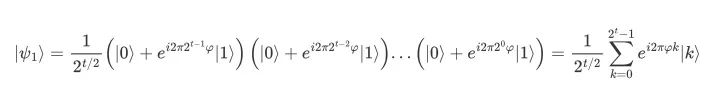
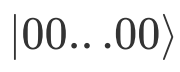 , k=2 表示
, k=2 表示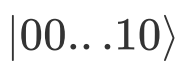 ,以此类推。
,以此类推。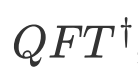 , 对
, 对 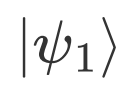 进行逆量子傅里叶变换可得
进行逆量子傅里叶变换可得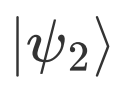
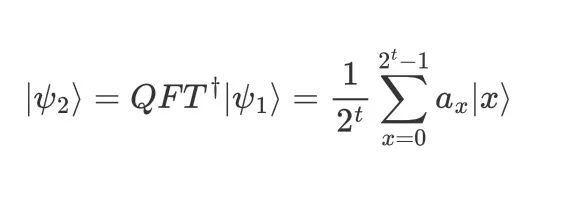
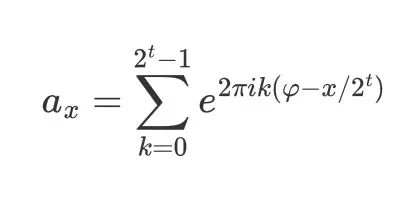
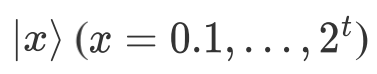 对应的概率幅 。由上式可得,当
对应的概率幅 。由上式可得,当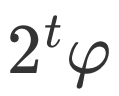 为整数,且满足
为整数,且满足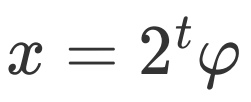 时,概率幅取最大值1,此时第一寄存器的末态可以精确反映
时,概率幅取最大值1,此时第一寄存器的末态可以精确反映 ;当
;当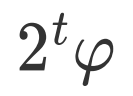
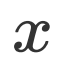 为
为 的估计,且t越大,估计精度越高。
的估计,且t越大,估计精度越高。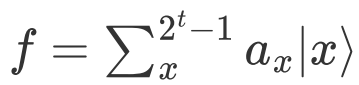 ,
, 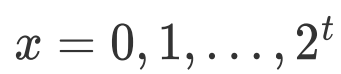 ;从中找到最大的概率幅
;从中找到最大的概率幅 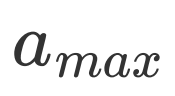 ,其对应的本征基矢
,其对应的本征基矢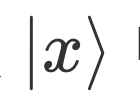 中的
中的 在除以
在除以  即为相位的估计值。
即为相位的估计值。QPE代码实现
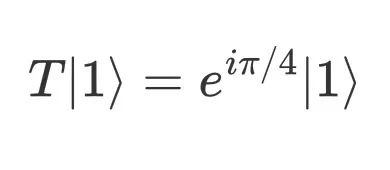
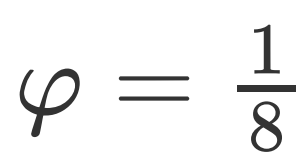 。
。from mindquantum import Circuitfrom mindquantum import Simulatorfrom mindquantum import UN, PhaseShift, qft, H, X, BARRIERimport numpy as np
Mindquantum.UN可以指定量子门,目标比特和控制比特,从而在线路中搭建门操作。因为我们已知
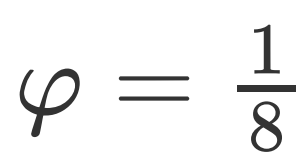 ,当
,当 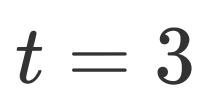 时可令
时可令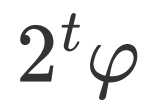 为整数,所以第一寄存器只需要3个比特即可准确估计;又已知
为整数,所以第一寄存器只需要3个比特即可准确估计;又已知 T门的本征态为
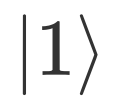 ,所以第二寄存器选择一个比特,即:我们需要搭建4比特线路,前
,所以第二寄存器选择一个比特,即:我们需要搭建4比特线路,前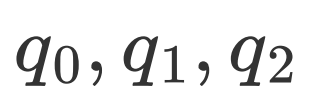 比特用于估计,属于第一寄存器;
比特用于估计,属于第一寄存器;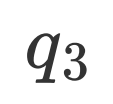 属于第二寄存器用于传入 T 算符的本征态。
属于第二寄存器用于传入 T 算符的本征态。UN对
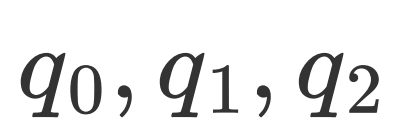 进行
进行 Hadamard门操作, 用
X门对
 进行翻转,得到
进行翻转,得到 T门的本征态
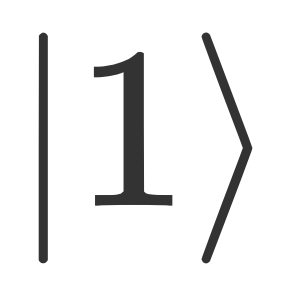 。
。n = 3c = Circuit()c += UN(H, n)c += X.on(n)c
 为目标比特,添加
为目标比特,添加 控制PhaseShift门
for i in range(n):c += PhaseShift({'phi': 2**i}).on(n, n-i-1)
c += BARRIERc += qft(range(n)).hermitian
 值传入并进行演化,得到末态
值传入并进行演化,得到末态sim = Simulator('projectq', c.n_qubits)phi = 0.125sim.apply_circuit(c,{'phi': 2*np.pi*phi})qs = sim.get_qs()
index = np.argmax(np.abs(qs))print(index)
12
index对应的
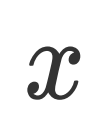 并不是真正的估计值,被
并不是真正的估计值,被 除之后也不是,因为测量结果中包括第二寄存器中的辅助比特,需要将
除之后也不是,因为测量结果中包括第二寄存器中的辅助比特,需要将index转成二进制后将辅助位剔除
bit_string = bin(index)[2:].zfill(c.n_qubits)[1:]print(bit_string)
100
theta_exp = int(bit_string[::-1], 2) / 2**n
0.125
 近似相等。
近似相等。本文为浙江大学闫家舜同学原创文章,欢迎大家投稿分享

文章转载自开源之夏,如果涉嫌侵权,请发送邮件至:contact@modb.pro进行举报,并提供相关证据,一经查实,墨天轮将立刻删除相关内容。






