项目经验分享：适用于求解分子基态与第一激发态能量的量子神经网络

1.  项目名称：

适用于求解分子基态与第一激发态能量的量子神经网络

2.  项目背景：

计算化学，顾名思义，就是基于量子力学的基本物理规律，利用数学方法通过计算机程序对化学体系进行模拟计算，以解释或解决化学问题。但是，要想真正通过计算模拟、运用基础理论去解决或解释化学问题，仅仅依靠精细的算法还是无法实现，必须还要借助于计算机的计算能力。可以说，量子化学的发展与计算机的发展息息相关。面对计算化学所涉及的巨大计算量，经典计算机在计算精度、计算尺寸等方面显得能力有限，这就在一定程度上限制了计算化学的发展。而费曼曾提出：可以创造一个与已知物理系统条件相同的系统，让它以相同的规律演化，进而获得我们自己想要的信息。费曼的这一猜想提示我们——既然化学所研究的体系是量子体系，我们何不在量子计算机上对其进行模拟呢？就目前而言，面对量子化学计算中所涉及到的如此惊人的计算量，经典计算机在计算精度、计算范围等方面十分有限。想要突破这一瓶颈，就必须依靠量子计算机强大的计算能力。因此，在量子计算机上实现量子化学模拟刻不容缓。

3.  方案描述：

就目前的量子计算机发展水平而言，可以通过变分量子特征值求解算法(Variational Quantum Eigensolver, VQE)^1–3，在量子计算机上实现化学模拟。该算法作为用于寻找一个较大矩阵 H 的特征值的量子与经典混合算法，不仅能保证量子态的相干性，其计算结果还能达到化学精度。

VQE的基本任务是制备参数化的量子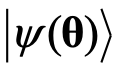并估计出给定分子的哈密顿量H的基态能量。其中，量子态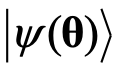是由参数化的量子电路(ansatz)生成。在这个过程中，我们采用经典的优化方法来寻找一组最优的参数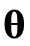，以最小化期望值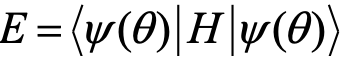，即为分子哈密顿量H的近似基态能量： 

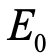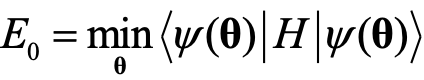       （1）

本项目需要利用mindquantum的框架编写出VQE的量子算法，并在模拟器上做数值模拟，用以求解分子基态与第一激发态能量，并将模拟结果与FCI的结果对照，以此来判断该量子算法的可靠性。

4.  时间规划

• 学习MindQuantum官方手册，熟悉MindQuantum软件的使用。

• 学习量子计算与量子化学的基础知识。

• 构建分子数据集，用于测试VQE方法的性能

• 根据MindQuantum中的样例VQE程序，学习VQE方法。

• 调研文献，了解VQE方法的前沿进展

• 根据文献中的内容，将文献中提出的新方法实现出来，并测试其效果

• 开发出一种新的VQE方法，并实现出来，测试其性能

1.  VQE方法简介

针对任意分子的基态(激发态)求解问题，本质上是求解其哈密顿量的低能本征值与本征态，任意分子体系的哈密顿量为：

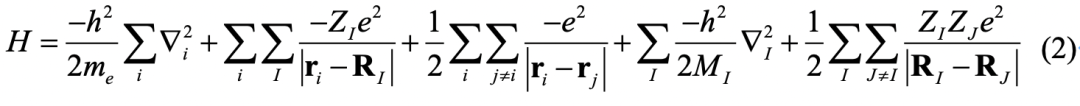
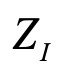表示原子核电荷的数量，r与R分别表示电子与原子核的空间坐标。采用原子单位制，取 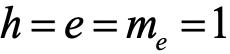，并采用Born-Oppenheimer近似，减掉后面两项，可以大大简化哈密顿量的本征值求解。对于一个有N个电子的(分子)体系，在经å典算法中，利用Hartree–Fock (HF)自洽平均场的方法，可以求解得到一组分子轨道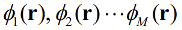，每个轨道对应一个能量，将能量由低到高依次取N(M>N)个分子轨道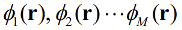，利用这 N个轨道构成的一个多体波函数，将这个多体波函数视为整个分子体系的基态，即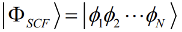，该方法称为单组态自洽场方法，也叫Hartree–Fock方法。

一般来讲，单组态自洽场方法没有考虑电子的Coulomb相关，所求得的体系的总能量要比实际高一些，一般将该能量差称之为相关能。为了准确地计算相关能，最直接的方法是组态相互作用方法(configuration interaction, CI)⁴，基态波函数的形式可以写成：

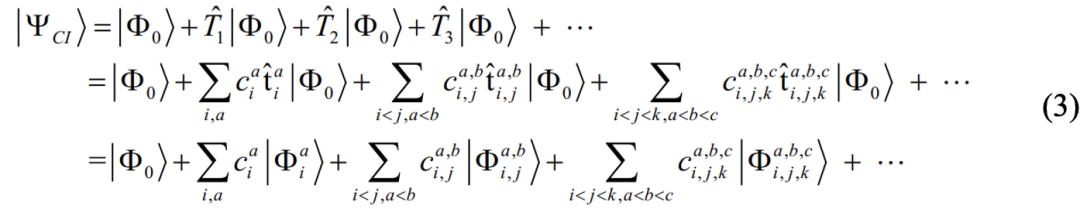
其中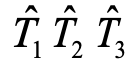，代表总的各类激发算符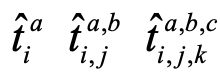，代表特定的激发算符，i j k表示参考态所占据的分子轨道，a b c表示参考态未占据的分子轨道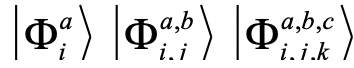，分别表示单激发、双激发以及三重激发态,

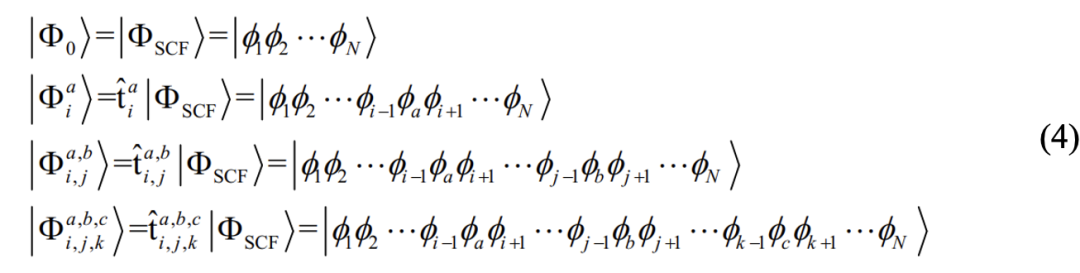
相比于单组态自洽场方法，组态相互作用方法考虑了更多不同的组态，理论上讲，分子体系的精确波函数需要由所有可能的组态给出。在此式的基础上，对系数做变分，求体系能量极小值，所得的波函数即为精确的波函数(不考虑相对论效应)。此为完全组态相互作用(Full Configuration Interaction, FCI)。FCI级别的波函数，在基组完备的条件下，是可以收敛至Schrödinger方程精确解的。然而，从上文公式中就可以看出，FCI方法的组态数量会随着电子数的增多而爆炸式增长，存储波函数的空间复杂度为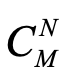，对个位数个电子还可以进行实际计算，对动辄几十上百成千上万个电子的实际体系而言，这种耗时增长速度是无法接受的。但是，如果利用量子计算机，将每个分子轨道的占据情况映射到量子比特的状态上，则可以大大减少存储波函数所需的比特数目。对于每一个分子轨道，存在两种情况，要么是被电子占据，或者未被占据，对于每一个组态，可以用如下的占据数表象来表述：

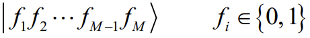
很自然的，可将每个分子轨道映射到一个量子比特，描述每个量子比特的状态需要两个基矢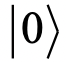，态与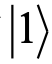态，可分别将这两个态对应于未被占据态以及占据态，对于每个组态，可以由量子比特表示为：

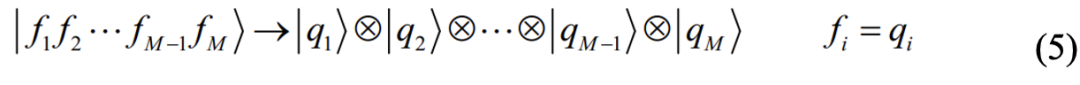
尽管分子体系的组态数目有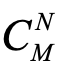个，但由于量子比特的叠加性质，M个量子比特可以表示为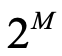个状态的线性叠加，因此只需要M个量子比特就能存储我们所要求得的波函数。将特定波函数映射到量子比特上之后，为了求得该波函数的能量，需要将哈密顿量H转化为量子线路的逻辑门组合，将逻辑门作用于目标量子比特上，然后通过多次测量求均值就能得到量子比特所表示的波函数的能量，具体操作方法如下。

将哈密顿量以二次量子化的形式表示：

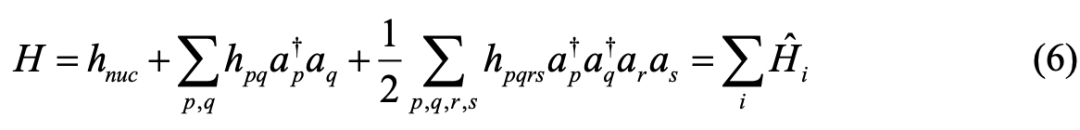
p q r s代表不同的自旋-空间轨道，根据二次量子化理论可知，在粒子数的表象下，哈密顿的形式为(6)式所示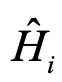，代表一项产生湮灭算符的组合。对于每一个产生湮灭算符，利用Jordan-Wigner变换，将其转化为相应的量子逻辑门组合：

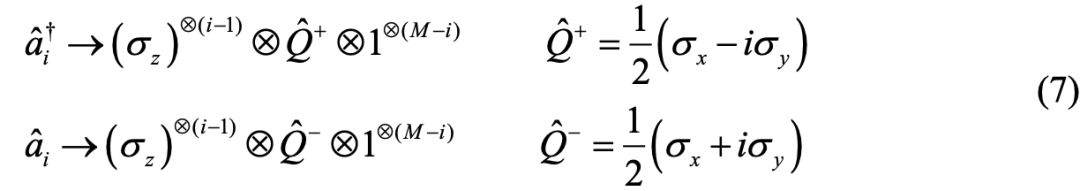
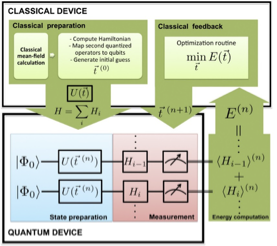
VQE方法流程图

将(7)式代入(6)式，就能得到H对应的量子线路。由此，我们找到了存储波函数及测量其能量的方法。基于变分量子算法的分子的基态(激发态)能求解，需要同时借助经典计算机和量子计算机，算法的大体流程如图2所示。该算法的核心思想是用一个经典优化器来训练一个含参的量子线路，确定一个目标函数，然后不断优化量子线路的参数，使得最终目标函数值达到最小。一般来讲，优化寻参这一步骤还是在经典计算机上完成的，目标函数的求解则是在量子计算机上完成的，因此该方法也被称作variational hybrid quantum-classical algorithm。

但现在为止，我们只是找到了可以有效存储任意波函数的方法，为了求解分子体系基态的能量，我们需要设计一套演化线路，使其能够将初始化的量子比特演化到体系基态所对应量子态。在本项目中，我分别采用了2种方法来构建ansatz线路，分别是UCCSD和QCCSD^5,6，下面分别介绍这些方法。

UCCSD-ansatz线路的构建方法是参考了量子化学中的耦合簇(CC)方法：定义一个波函数参考态(HF态)，以e指数算子的形式将激发算符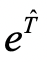作用于参考态上。但是，由于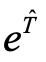不是一个幺正算符，而量子计算机的逻辑门只支持幺正算子，故不能再量子计算机上做的演化操作。不过，若将激发算符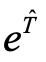改为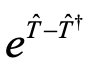，该激发算符就满足幺正性，就可以通过量子线路实现出来，该方法即为酉耦合簇方法(UCC)，如果只考虑单激发与双激发的情况，对应的线路即为UCCSD-ansatz。

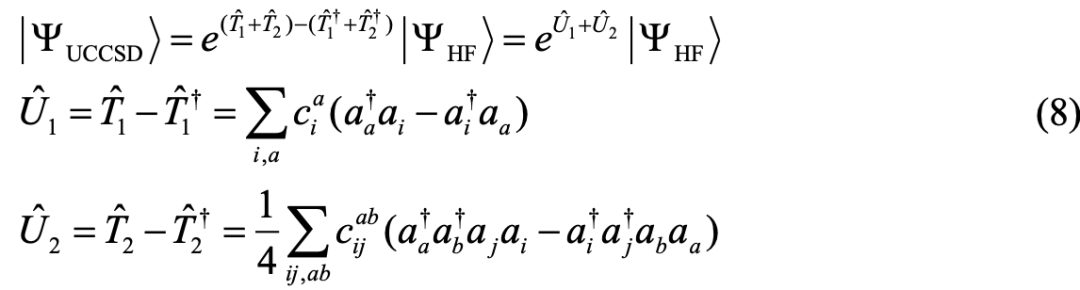
具体到如何用量子线路来实现UCCSD-ansatz，还需要将算子转化为量子计算机支持的基本量子逻辑门。首先，根据上述的Jordan-Wigner 变换将每个粒子产生湮灭算符转化成对应的Qubit线路，即：

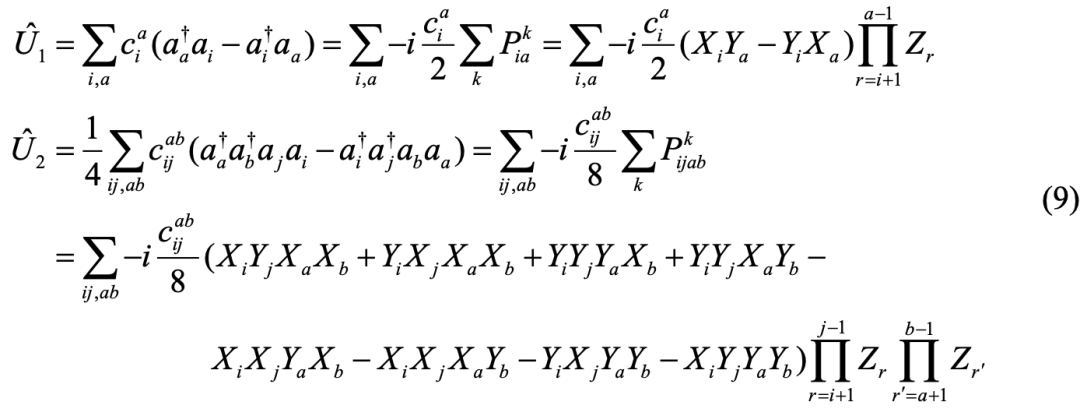
其中，X、Y、Z分别对应于三个泡利矩阵逻辑门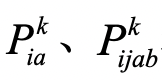，表示不同X、Y、Z逻辑门序列。在此基础上，利用Trotter分解，将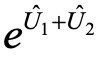分解为每个不同X、Y、Z逻辑门序列的连乘组合：

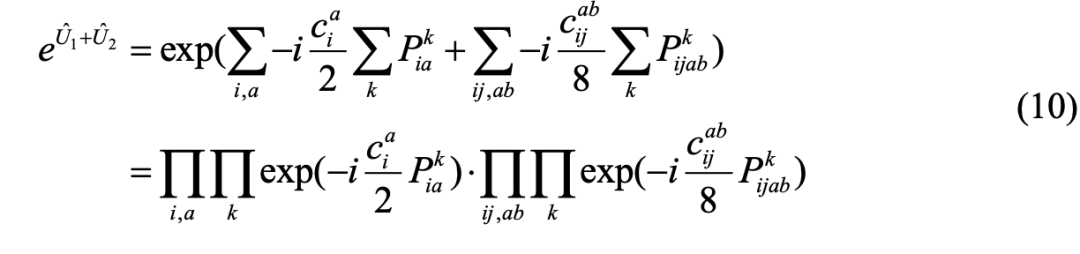
对于分解后的每项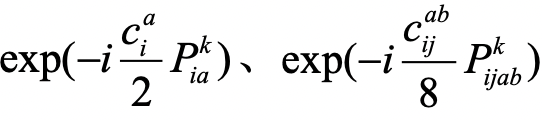，存在相应的方法将其最终分解为硬件上所支持的基本量子逻辑门。

可以看到，在UCC形式的ansatz(21式)中存在大量Z逻辑门序列，该序列的存在会大大加深线路的深度，并且会增加双比特逻辑门的消耗，为了更进一步降低计算资源的消耗，我们可以在UCCSD-ansatz的基础上直接将操作算符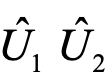中的Z门删掉，此时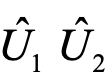中每一项不再表示费米子的操作算符，因为不满足相应的费米子算符的对易性质，这些算符更像是直接作用于量子比特：将一个量子比特上的占据态激发到另一个量子比特上，所以这种方法也叫QCC-ansatz，具体形式如下：

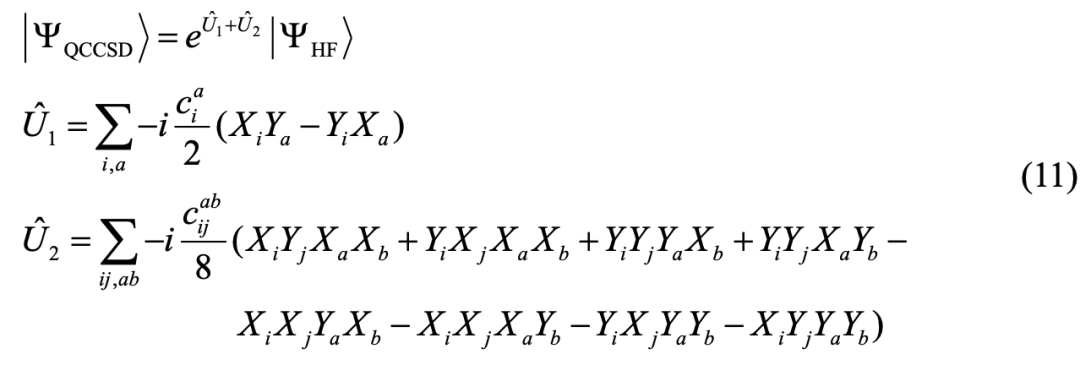
总结一下，对于基态的求解，VQE 的整体流程如下：

1. 构建一个含参的量子线路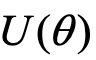，用于制备试探波函数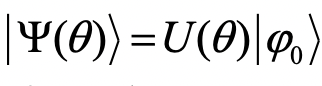

2. 用量子计算机测量出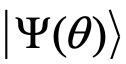的能量期望

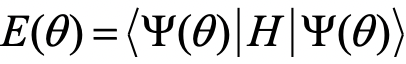
3. 为不断降低能量，利用经典优化器更新参数，返回第2步，直至收敛

对于激发态的计算，我们则是用了正交约束的方法7,8，该方法的其它步骤与上述的VQE方法基本一致，只是将哈密顿量改为：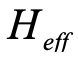

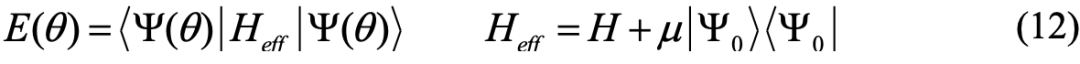
这相当于从哈密顿量的谱分解中，将基态对应的本征能量抬高，从而使得的第一激发态对应了的基态，此时计算能量期望值时还需要测量基态和第一激发态的overlap

2.  编程框架简介

•  MindQuantum

MindQuantum是结合MindSpore和HiQ开发的量子机器学习库，支持多种量子神经网络的训练和推理。得益于华为HiQ团队的量子计算研发能力和MindSpore高性能自动微分能力，MindQuantum能够高效处理量子机器学习、量子化学模拟和量子优化等问题，为广大的科研人员、老师和学生提供了快速设计和验证量子机器学习算法的高效平台。

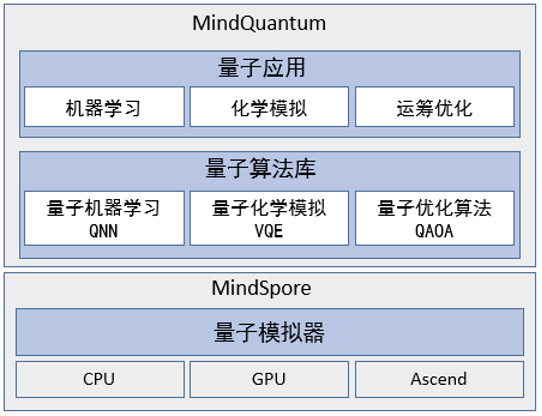
MindQuantum架构

• OpenFermion

OpenFermion是Google主导的量子计算开源软件包，用于编译和分析量子算法来模拟费米子系统，包括量子化学，这是第一个能够将化学和材料科学问题转化为可以在现有平台上执行的量子线路的开源软件。在OpenFermion开发之前，量子算法开发人员需要学习大量的化学知识，并且要编写大量的代码，除了要将其它的代码组合在一起，甚至连最基本的量子模拟也涵盖在内，这就大大增加了算法开发人员的工作复杂度。OpenFermion的出现大大减轻了量子算法开发人员的工作量，使其可以将更多的精力用于开发算法本身。

3.  代码编写

根据VQE的基本原理以及上述所设计出的4种ansatz结构(UCCSD、QCCSD、k-UpCCGSD、k-QpCCGSD)，使用MindQuantum的编程框架，我分别编写出了不同的用以求解分子基态与第一激发态能量的量子神经网络，UCCSD-VQE的代码如下所示：

import os
import numpy as np
from openfermionpyscf import run_pyscf
from mindquantum import Circuit, X, RX, Hamiltonian
from mindquantum.circuit import generate_uccsd
from mindquantum.nn import generate_pqc_operator
from mindspore import Tensor
from openfermion.chem import MolecularData
from scipy.optimize import minimize


os.environ['OMP_NUM_THREADS'] = '4'


dist = 1.0
geometry = [
    ["H", [0.0, 0.0, 0.0]],
    ["H", [dist, 0.0, 0.0]],
    ["H", [dist * 2.0, 0.0, 0.0]],
    ["H", [dist * 3.0, 0.0, 0.0]],
    ["H", [dist * 4.0, 0.0, 0.0]],
    ["H", [dist * 5.0, 0.0, 0.0]],
]
basis = "sto3g"
spin = 0


molecule_of = MolecularData(geometry, basis, multiplicity=2 * spin + 1)
molecule_of = run_pyscf(molecule_of, run_scf=1, run_ccsd=1, run_fci=1)
molecule_of.save()
molecule_file = molecule_of.filename


hf_state_circuit = Circuit([X.on(i) for i in range(0,molecule_of.n_electrons,1)])
ansatz_circuit, _, _, hamiltonian_QubitOp, _, _ = generate_uccsd(molecule_file, th=-1)
total_circuit = hf_state_circuit + ansatz_circuit
init_amplitudes = [0.0 for j in range(len(total_circuit.para_name))]
molecule_pqc = generate_pqc_operator(["null"], total_circuit.para_name, RX("null").on(0) + total_circuit, Hamiltonian(hamiltonian_QubitOp))


def energy_obj(n_paras, mol_pqc):
    encoder_data = Tensor(np.array([[0]]).astype(np.float32))
    ansatz_data = Tensor(np.array(n_paras).astype(np.float32))
    e, _, grad = mol_pqc(encoder_data, ansatz_data)
    return e.asnumpy()[0, 0], grad.asnumpy()[0, 0]


res = minimize(energy_obj,
    init_amplitudes,
    args=(molecule_pqc, ),
    method='bfgs',
    options={'disp': True, 'return_all': True},
    jac=True,
    tol=1e-6)
    
print("VQE energy with UCCSD ansatz:{}".format(float(res.fun)))
print("Corresponding parameters:{}".format(res.x.tolist()))

MindQuantum支持生成UCCSD线路，可以在代码中直接调用相应的接口(generate_uccsd函数)。对于QCCSD-ansatz，我自己编写了生成相应量子线路的接口，具体可以参考源代码中的qcc_excitation_circuit.py 文件，调用方法也类似，在此就不做赘述。关于第一激发态的求解，代码如下所示，使用QCCSD-VQE的方法来求解氢分子的第一激发态的能量。

import random
import numpy as np
from openfermion.chem import MolecularData
from openfermion.transforms import get_fermion_operator, jordan_wigner
from mindquantum import Circuit, X, RX, RY, Hamiltonian, StateEvolution
from mindquantum.nn import generate_pqc_operator
from mindquantum.parameterresolver import ParameterResolver
from mindspore import Tensor
from qcc_excitation_circuit import qccsd_singlet_generator, add_prefix_to_circuit
from scipy.optimize import minimize


def circuit_grad(qubit_circuit, paras_data, obj_grad_paras):
    obj_paras_grad = []
    state_array = StateEvolution(qubit_circuit).final_state(paras_data)
    for obj_grad_para in obj_grad_paras:
        para_grad = 0.0
        for gate_idx, gate in enumerate(qubit_circuit):
            grad_circuit = Circuit()
            grad_circuit += qubit_circuit
            if gate.coeff is None:
                continue
            if isinstance(gate.coeff, ParameterResolver) == False:
                continue
            if gate.coeff.para_name[0] == obj_grad_para:
                add_gate = RY(np.pi).on(gate.obj_qubits, gate.ctrl_qubits)
                grad_coeff = 0.5 * gate.coeff.para_value[0]
                grad_circuit.insert(gate_idx, add_gate)
                state_array0 = StateEvolution(grad_circuit).final_state(paras_data)
                para_grad += grad_coeff * state_array0[0] * state_array[0] * 2.0
                continue
        obj_paras_grad.append(para_grad.real)
    return np.array(obj_paras_grad)


def energy_obj(n_paras, mol_pqc, ansatz_circuit, ground_state_circuit, ground_state_paras):
    encoder_data = Tensor(np.array([[0]]).astype(np.float32))
    ansatz_data = Tensor(np.array(n_paras).astype(np.float32))
    e, _, energy_grad0 = mol_pqc(encoder_data, ansatz_data)
    energy = e.asnumpy()[0, 0]
    energy_grad = energy_grad0.asnumpy()[0, 0]
    overlap_circuit = ansatz_circuit + ground_state_circuit.hermitian
    pr = dict(zip(overlap_circuit.para_name, list(n_paras) + ground_state_paras[::-1]))
    state_array = StateEvolution(overlap_circuit).final_state(pr)
    overlap = float(abs(state_array[0]))**2
    overlap_grad = circuit_grad(overlap_circuit, pr, ansatz_circuit.para_name)
    overlap_punish_factor = 10.0
    f = energy + overlap_punish_factor * overlap
    grad = energy_grad + overlap_punish_factor * overlap_grad
    return f, grad


dist =1.0
depth = 1
geometry = [["H", [0.0, 0.0, 0.0]],["H", [dist, 0.0, 0.0]],]
basis = "sto3g"
spin = 0
multiplicity = 2 * spin + 1
description = '{:.3f}'.format(dist)
molecule = MolecularData(geometry, basis, multiplicity, description=description)
molecule.load()
hamiltonian_InteractionOperator = molecule.get_molecular_hamiltonian()
hamiltonian_FermionOperator = get_fermion_operator(hamiltonian_InteractionOperator)
hamiltonian_QubitOperator = jordan_wigner(hamiltonian_FermionOperator)
hamiltonian_QubitOperator.compress()


hf_state_circuit = Circuit([X.on(i) for i in range(0,molecule.n_electrons,1)])
qccsd_circuit = qccsd_singlet_generator(molecule.n_qubits, molecule.n_electrons)
total_circuit = hf_state_circuit + qccsd_circuit
ground_state_circuit = add_prefix_to_circuit(total_circuit, 'g0')
total_circuit = hf_state_circuit + qccsd_singlet_generator (molecule.n_qubits, molecule.n_electrons)
init_amplitudes = [random.random() for j in range(len(total_circuit.para_name))]
ground_state_amplitudes = [-2.5437139710730514e-05, -0.3527054024157375]
molecule_pqc = generate_pqc_operator(["null"], total_circuit.para_name, RX("null").on(0) + total_circuit, Hamiltonian(hamiltonian_QubitOperator))


res = minimize(energy_obj,
    init_amplitudes,
    args=(molecule_pqc, total_circuit, ground_state_circuit, ground_state_amplitudes),
    method='bfgs',
    options={'disp': True, 'return_all': True},
    jac=True,
    tol=1e-6)
    
print("VQE energy with QCC ansatz:{}".format(float(res.fun)))
print("Corresponding parameters:\n{}".format(res.x.tolist()))

可以看到，求解第一激发态必须要知道基态的线路参数，因为要将试探波函数与基态波函数做投影，投影值会伴随一个惩罚项，该惩罚项会升高测量的能量，从而促使线路朝着与基态完全正交的方向来优化，而即与基态正交同时能量最低的态便是第一激发态。

根据以上的代码，我分别测试了H2、H4、H6、LiH、H2O、BeH2的解离曲线，基组取sto-3g，将UCCSD、QCCSD的计算结果与HF、CCSD和FCI的结果做对比，结果如下图所示

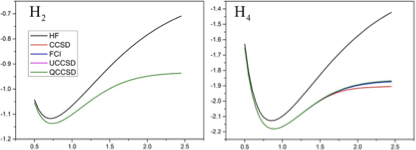
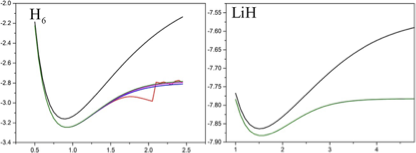
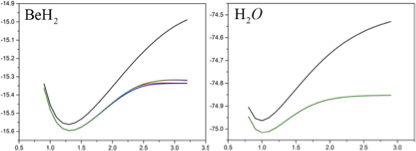
分别使用HF、CCSD、FCI、UCCSD、QCCSD方法计算H2、H4、H6、LiH、H2O、BeH2的解离曲线

可以看到，无论是UCCSD，或是QCCSD，在分子的平衡位置及其附近的计算结果都很准确，在远离平衡位置的结构计算会出现一点微小的偏差，总体来说计算结果与FCI的结果基本一致。关于第一激发态的计算，我测试了氢分子体系，发现VQE的结果与FCI的结果完全一致，都是-0.74587Ha，说明方案的可行性以及代码的正确性。我已将现有工作的相关代码上传到了Gitlab平台上，地址为：

https://gitlab.summer-ospp.ac.cn/summer2021/210610350/-/tree/main/

本项目难度较高，完成本项目需要学习大量的理论知识，既要有量子计算方面的基础，同时还要有量子化学方面的基础，总之需要一定的理论功底才能读懂本项目相关的科研论文，同时还要具备一定的编程技巧才能开展项目工作。但好在自己本身的研究方向就是量子计算在量子化学中的应用，所以在开始项目的阶段，本身就具备了一定的理论功底，但即便如此，项目过程中，还是感觉略有吃力，自己想在前人工作的基础做出一点创新真的很难，但是感谢项目导师给予我的建议与帮助，往往导师的几句话，就点明了我的方向，当我在代码编写的过程中遇到了一些我无法理解的bug，导师也为我耐心地排查问题并寻找解决方案。总之，遇到困难可以尝试与导师沟通交流，比自己闭门造车的效率要高太多了。

• 善于应用工具

项目开始之前，我本身就具备projectq的应用基础，所以我开始想的就是直接用projectq来编写项目代码，没必要去新学mindquantum的编程框架，但后来通过我对mindquantum样例代码的阅读，发现mindquantum确实会大大简化量子线路的设计，同时在线路参数求导方面也有着巨大的优势，所以我后来果断采用了mindquantum的编程框架，在这里也要感谢mindquantum的开发团队，mindquantum的出现大大方便了我们量子计算研究者的工作，让我们算法开发变地更容易。

这次活动促进了开源软件的发展，也为开源社区贡献了新的活跃度，推进MindSpore开源生态的发展，也推动了在校学生积极参与开源社区并做出贡献；

感谢 @开源之夏主办方 为这次活动提供的平台与机会；

感谢张老师、徐老师与苑老师对我的帮助，使得我能顺利完成项目。