首先感谢王先胜百忙之中完成算法约稿。
在《新媒体变现之三--介绍搜索竞价排名广告Sponsored Search》一文中,介绍了付费搜索的业务场景和通常的账号体系结构。其中, 关键字的出价对广告主而言是很重要的一环, 本文在此基础上简单介绍几种自动出价算法。
出价问题通常抽象为背包问题, 需要解决的问题定义如下:
给定预算B, 竞价N个关键字k1, k2, ...kn,每个关键字出价b1, b2, …bn, 每个关键字有M个广告位,已知每个广告位的cpc(cost per click)、ctr(clickthrough rate,点击率)以及关键字的展示量impression(根据之前的统计数据),求b1, b2, ...bn,使w(k,b)之和小于B, 且收益v(k,b)最大。其中v(k,b)表示关键字k出价b时获得的收益,可以是广告带来的纯收入或者简单的广告点击量( Clicks( k, b) = CTR( k, b) * Impr( k, b)), w(k,b)表示对应的花费。
均价算法:
我们先考虑简化的情况,即只竞价一个关键字的情况。
假设有M个广告位,广告位i的点击率为ctr(i),点击收费cpc(i),则期望花费cost(i) = ctr(i) * cpc(i)。以cost为横坐标, ctr为纵坐标,得到二维坐标系下的一系列点(成本-收益图), 求这些点的凸包。以单次点击预算B画直线x=B,与凸包上边界相交的两个端点即为需要的出价, 按线段比率随机出价。例如下表所示的广告位

得到的成本收益图如下: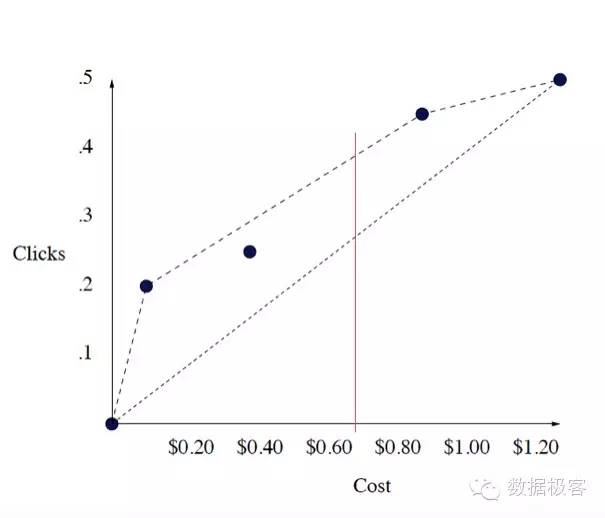
虚线框表示凸包, 红线表示预算$0.70时出价,其与上边界相交的边上的两个端点即为出价。
如果竞价多个关键字,但是出价相同, 也可以使用此算法, 此时上图由各个关键字的广告位<cost, clicks>复合而成。
遗传算法:
如果出价多个关键字,每个关键字有多个广告位,则是典型的多选择背包问题,其时间复杂度为O(K^M),其中K为关键字个数,M为每个关键字的广告位数目,算法复杂度为指数级别。当K、M很小时,简单的组合算法即可求出最优解;若预算B很小,则可用动态规则思路解决。但若K、M、B较大,则需要使用近似算法。遗传算法便是其中一种。
遗传算法(Genetic Algorithm)是模拟达尔文生物进化论的自然选择和遗传学机理的生物进化过程的计算模型,是一种通过模拟自然进化过程搜索最优解的方法。初始种群经过多次迭代进化,优胜劣汰逐步逼近最优解。主要由以下步骤组成:
init: 随机生成若干组出价,每组出价称为一个个体,每个个体是出价问题的一组解,比如<b1, b2,...bn>即为一个个体。个体的优劣由适应度(fitness)函数计算,这里一般就是上文所述的收益v(k,b)之和。这些个体组成初始的第一代种群。
selection: 从上一代的个体里随机选择交配个体, 选择算法一般使用 Weighted Roulette Wheel Selection (Weighted RWS) 或者 Stochastic Universal Sampling (SUS)算法, 这些算法能使优秀的个体有更多的机会被选中。
crossover: 每两个个体交配, 分别取其中的部分值(出价bi)生成两个新的个体。这些新的个体形成下一代的种群,继续往下进化。
elitism: 为了保证特别优秀的个体解不被稀释, 给予其特权,不用交配直接加入下一代种群,这个比例一般为最优秀的一对个体。
mutation: 新一代种群中的个体按一定概率(如1%)变异,随机更改其中的部分出价,防止局部最优。
当迭代了若干代或者两代之间的收益不再提高时,算法结束, 输出适应度最高的个体作为出价。
在线算法:
下面介绍一种在线实时出价算法,此算法更多的适用于流式输入请求的实时出价。这里仅考虑只有一个广告位的情况。
假设当前需要出价的关键字广告点击获得的收益为V,已经使用的预算比率为z(t),则t时刻出价:
b(t) = V/( 1 + f(z) ), 其中f(z) = (U*e/x)^z (x/e),x为很小的正数,e为自然对数, U=V/bmin, bmin是搜索平台规定的最小出价。
从公式可以看出,此出价只和当前已使用的预算比率及广告收益有关,不需要知道ctr和其他出价者的出价,计算代价小,适合实时出价。可以证明, 此出价具备很高的近似最优比。具体证明过程可以参考相关论文。
参考文献:
1. 均一出价: Budget Optimization in Search-Based Advertising Auctions, Jon Feldman S. Muthukrishnan, Martin P´al, Cliff Stein.
2. 遗传算法: The Adomaton Prototype: Automated Online Advertising Campaign Monitoring and Optimization, KYRIAKOS LIAKOPOULOS, STAMATINA THOMAIDOU, MICHALIS VAZIRGIANNIS.
3. 在线算法: Budget Constrained Bidding in Keyword Auctions and Online Knapsack Problems, Yunhong Zhou, Deeparnab Chakrabarty, Rajan Lukose






